RBA Annual Conference – 2004 Discussion
Gordon de Brouwer[1]
There are few analytical areas more basic and important for a central bank than measuring and modelling inflation. The Heath-Roberts-Bulman paper makes an important contribution to understanding the complexity in measuring and modelling inflation, with particular reference to Australia. On the measurement issue, Alex, Ivan and Tim set out two criteria to determine the usefulness of measures of underlying inflation, and they apply them to the Australian data. On the modelling issue, they estimate mark-up and Phillips curve models for their preferred measure of underlying inflation. They show that the effect of the exchange rate on consumer price inflation has moderated substantially over the past decade and that inflation has become increasingly harder to model; it behaves like a ‘constant’, although it is subject to demand pressures. They argue that this is an outcome of low inflation.
The paper raises a raft of issues, some technical and some policy-based. Alex, Ivan and Tim have provided a clean and rigorous technical analysis. I would like to discuss issues that arise from both parts of the paper in turn, and look at some of the policy implications that arise from the analysis in the paper. On the issue of inflation measurement, my main point is that other criteria are also relevant in selecting underlying measures of inflation. On the modelling side, I don't think that the failure of inflation modelling is as overwhelming as the authors suggest: statistical work using other definitions of underlying inflation, imperfect as they are, does not seem to suffer the extent of instability exhibited with their preferred definition of underlying inflation. And the decline in the pass-through of exchange rate changes apparent in statistical work may be, at least to some extent, because relatively more adjustment has been occurring through quality changes than price changes, due to broader structural change in the Australian economy.
The use of underlying measures of inflation
Alex, Ivan and Tim look at 102 measures of underlying inflation, although they only report some test results for 13. These measures include a mix of exclusion-based measures (dropping volatile components) and statistically-adjusted measures. They argue that a good measure of underlying inflation is one which is unbiased with respect to the actual CPI and one which predicts the actual CPI but is not predicted by it. The results don't stack up all that well in general across different time periods. And they look to be a bit worse for exclusion-based measures (which is a bit disappointing from a policy perspective because I suspect that exclusion-based measures are easier to explain to non-economists). Nevertheless, the authors make a judgement call that pragmatic use of the underlying measures is important in understanding what is going on with inflation at particular points in time.
That judgement looks right. The rationale for looking at underlying measures of inflation is that the headline CPI inflation statistic can be a distorted indicator of the true inflation impulse in an economy. Focusing on the ‘underlying’ bit is an attempt to ‘wash out’ the misleading signal in the statistics. Accordingly, this sort of exercise is, and remains, a necessary one for serious analysis of inflation.
But, while it is necessary, it has probably become less important, at least for that part of the debate which is in the ordinary public domain. One reason is pointed out by the authors themselves. For the past 13 years or so of low and less variable inflation, the noise in the inflation statistics has, not surprisingly, become smaller. With less noise, the inflationary impulse is easier to identify and the need for underlying measures is less than it was. The authors seem attached to the measures of underlying inflation – indeed, they explicitly refer to the full sample results to support their assessment that underlying measures still matter a lot. But if Australia is now in a low-inflation world, then the experience of the past decade, not of their full sample, is what matters. And in this period the evidence of the usefulness of underlying measures is much weaker.
Another reason why underlying measures are less important now is that headline CPI inflation has been calculated on an acquisitions basis since 1998, and the inflation target agreed between the Treasurer and the Governor is now headline CPI inflation, not underlying inflation. The target is a medium-term one. This is important since the medium term itself tends to wash out the noise in headline inflation. The authors refer to how the authorities can use measures of underlying inflation to communicate with the public about the inflationary impulse in the economy. To my mind, discussion of inflation is now best done in the main with reference to the targeted measure itself, and not underlying measures, especially since these measures are biased indicators of headline CPI inflation in the low-inflation environment (albeit mostly insignificant). When there is noise that distorts the information content of the inflation statistic, then that should be explained as such.
Of course, this does not mean that analysis of underlying inflation is unnecessary. Measures of underlying inflation have lost their policy prominence but they still have to be assessed in the engine rooms of economic analysis in order to inform policy-makers' judgement of whether the inflation statistics at any point in time are a reliable guide to the inflationary impulse. It is helpful for economists elsewhere to know the substance of the work being done in the central bank on this; the paper is particularly useful in this respect.
The choice of which underlying measure to use is also, I suspect, broader than the two technical criteria that the authors set out and test. Other aspects matter. Depending on the target audience, it helps if the underlying measure used can be readily understood. Economists can surely understand the logic of the statistically-derived measures but the general public might understand the exclusion-based measures better.
And the choice of underlying measure for modelling, forecasting or policy analysis will be determined by the extent to which that particular measure is useful for that task. The measure which best meets the criteria set out by the authors might not in fact be the best for modelling, forecasting or policy analysis. One possible limitation of statistically-based measures of underlying inflation, for example, is that they may exclude valuable economic information. If the price changes or volatility are purely random, then no economic information is lost. But if the volatility is systematic, reflecting a common ‘shock’, then some economic information is lost. One such shock is a substantial movement in the exchange rate, which leads to the second part of the paper: inflation modelling.
Modelling inflation
The second part of the paper is concerned with modelling inflation, especially with pass-through of the exchange rate to prices. The economic story that the authors tell is that first-stage pass-through (from the exchange rate to import prices in Australian dollars) is full and quick, but that second-stage pass-through (from import prices to consumer prices) basically halved from the 1980s to the 1990s, a result they attribute to the success of inflation targeting in Australia.
But they temper this result by reporting that the performance of standard inflation equations has deteriorated significantly over this period. It is clear from the paper that the equations estimated over the 1990s are basically a mess. With respect to the mark-up model of inflation, the explanatory power halves (the adjusted R-squared falling from 0.51 to 0.25) when data from the early 1990s are excluded, and in the 1990s the error-correction term becomes insignificant and the rejection of linear homogeneity of consumer prices with respect to import prices and unit labour costs becomes quite spectacular. With respect to the import-price augmented Phillips curve, the import price variables in the equation are not statistically significant (which begs the whole question of why that model is used in the first place) and the explanatory power of the equation basically disappears when the sample is restricted to the past decade.
The authors argue that it is harder to estimate equations under low and stable inflation. But it is not clear that this is a necessary consequence of low inflation; low and stable inflation could be the result of low and stable growth in the driving variables. There could be other things going on which cause the results that the authors report. There are three other possibilities that I would like to canvas here. The problems with estimation might be caused by the particular measure of underlying inflation being used. There could be new divergences in the statistical measure of labour costs or import prices used from ‘true’ labour costs or import prices. Or it might be a quirk of a particular econometric methodology.
To explore this, Table 1 presents two sets of indicative results. Columns (1) to (3) show results estimated from a dynamic single equation error-correction model – along the lines of de Brouwer and Ericsson (1998) – for the weighted median measure of inflation over three sample periods: March quarter 1990 to March quarter 2004, March quarter 1993 to March quarter 2004, and March quarter 1990 to June quarter 2002. Columns (4) to (6) show the results over the same sample periods respectively for an exclusion-based measure of underlying inflation – actual CPI less interest rate charges, selected volatile items (like fresh food and energy) and a number of non-market items (such as health and education), which is equivalent to the Australian Bureau of Statistics' old measure of Treasury underlying inflation.[2] Linear homogeneity is imposed in these estimations – that is, the coefficients on unit labour costs, import prices, and oil prices are required to sum to one. The bottom row in Table 1 reports the marginal significance of the Wald statistic: a number equal to or less than 0.05, for example, indicates rejection of the null hypothesis of linear homogeneity at the 5 per cent level of significance.
| Inflation as weighted median | Inflation as Treasury underlying | ||||||
|---|---|---|---|---|---|---|---|
| 1990:Q1– 2004:Q1 (1) |
1993:Q1– 2004:Q1 (2) |
1990:Q1– 2002:Q2 (3) |
1990:Q1– 2004:Q1 (4) |
1993:Q1– 2004:Q1 (5) |
1990:Q1– 2002:Q2 (6) |
||
| Constant | 0.06 [0.00] |
0.04 [0.24] |
0.06 [0.00] |
0.05 [0.00] |
0.10 [0.04] |
0.05 [0.01] |
|
| Adjustment parameter |
−0.07 [0.00] |
−0.05 [0.16] |
−0.08 [0.00] |
−0.07 [0.00] |
−0.12 [0.01] |
0.06] [0.00] |
|
| Long-run coefficient on import prices |
0.11 [0.13] |
0.19 [0.24] |
0.17 [0.04] |
0.31 [0.00] |
0.20 [0.01] |
0.30 [0.01] |
|
| Implied long-run coefficient on unit labour costs |
0.84 | 0.73 | 0.79 | 0.64 | 0.76 | 0.65 | |
| Long-run coefficient on oil prices |
0.05 [0.00] |
0.08 [0.07] |
0.04 [0.00] |
0.05 [0.00] |
0.04 [0.00] |
0.05 [0.01] |
|
| GST dummy | 0.027 [0.00] |
0.027 [0.00] |
0.027 [0.00] |
0.021 [0.00] |
0.021 [0.00] |
0.021 [0.00] |
|
| Change in ulc (t) |
0.08 [0.01] |
0.06 [0.14] |
0.07 [0.03] |
0.07 [0.03] |
0.09 [0.04] |
0.07 [0.02] |
|
| Change in ulc (t–5) |
10.05 [0.11] |
0.04 [0.25] |
0.06 [0.06] |
0.05 [0.07] |
0.05 [0.16] |
0.06 [0.09] |
|
| Output gap (t) | 0.10 [0.00] |
0.09 [0.04] |
0.11 [0.00] |
0.09 [0.00] |
0.15 [0.00] |
0.09 [0.00] |
|
| Adjusted R-squared |
0.83 | 0.86 | 0.85 | 0.80 | 0.83 | 0.80 | |
| Homogeneity restriction |
[0.42] | [0.54] | [0.87] | [0.52] | [0.45] | [0.62] | |
| Notes: The number in square brackets is the marginal significance; bold numbers indicate null hypothesis rejected at the 10 per cent level; linear homogeneity is imposed and tested. | |||||||
There are four results of note:
- The import price variable becomes insignificant in the weighted median underlying inflation equation in the 1990s when the endpoint is 2004. But import prices are still significant when the endpoint in this specification is 2002 (Column 3), implying that observations from the last few years might be the problem.
- The equation breaks down, along the lines outlined by Alex, Ivan and Tim, when underlying inflation is defined as the weighted median but it does not appear to do so when underlying inflation is defined on an exclusion basis as the Treasury underlying series. How underlying inflation is defined seems to matter.
- Linear homogeneity is not rejected in this estimation, either for the weighted median or the Treasury underlying series. This is not consistent with the results of Alex, Ivan and Tim. The puzzle is that different econometric methodologies seem to yield different outcomes with respect to linear homogeneity for the weighted median. (Linear homogeneity is not rejected for the Treasury underlying series in estimations, but it is in the estimations which include the early 1990s.) Economists tend to be uncomfortable with an overwhelming rejection of linear homogeneity – the trends in costs and prices cannot diverge in the long run for, if they do, the economic system explodes or implodes. Spectacular rejection of homogeneity might be a signal that something is wrong with the data or estimation.
- The degree of exchange rate pass-through does appear to have lessened somewhat over the past decade or so. When the early 1990s are excluded from the sample, for example, the long-run coefficient on import prices declines from 0.3 to 0.2 for the Treasury underlying series.
One obvious difference between the results presented in the paper and those outlined above is the measure of underlying inflation. The weighted median and the Treasury underlying inflation measure have moved much the same way over the past few decades, except in the past few years. The Treasury underlying measure has fallen in the past year or so but the weighted median has not; as shown in Figure 1, the Treasury underlying measure was about 1.4 per cent in the March quarter 2004, compared to 2.3 per cent for the weighted median.
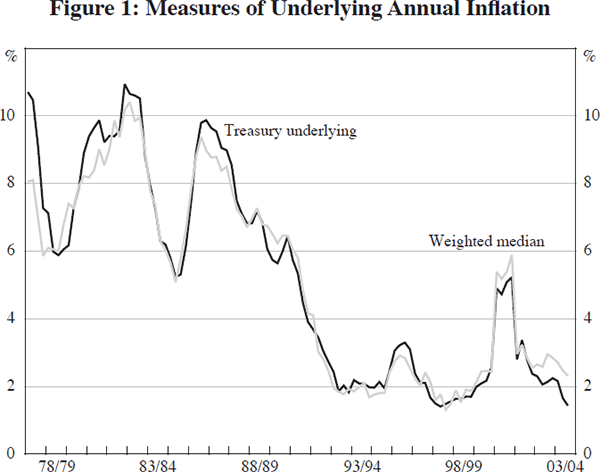
It is not surprising that a mark-up model using the Treasury underlying series will tend to perform better because that measure has fallen much more at a time of sharp currency appreciation – about 45 per cent over the past two years. The puzzle is why the gap has emerged between the weighted median and this particular exclusion-based measure.
One conjecture is that the prices which have changed the most are those on imported goods. Against a background of low overall price volatility, imported prices have been the ones that have moved most, and so they are likely to have been the ones cut out of the statistically-based measure.[3] By contrast, these goods and services are not the ones excluded from the Treasury underlying measure. Pass-through is less apparent in statistical work based on the weighted median measure which only partially reflects the impact of falling import prices over the more recent period. The collapse of the weighted median inflation equation in the past few years is consistent with this explanation.
It appears that systematic influences are being removed from the statistically-based measures of inflation. Given that the overall noise in inflation is now lower, the risk of removing systematic effects is now greater. If this is the case, then the statistically-based measures of underlying inflation might need to be used with caution for economic modelling, particularly when inflation is low and stable. In this instance, the systematic influence is the effect of exchange rate movement, but it could also apply to other systematic influences.
To the extent that statistically-based measures remove systematic influences of the exchange rate on inflation, the estimated pass-through parameter will be biased downwards, underestimating the ‘true’ extent of pass-through. This might explain why the pass-through parameter is notably lower for the weighted median (an average of about 0.15) than the Treasury underlying measure (an average of about 0.25).
This does not mean that the Treasury underlying measure is necessarily the best measure of underlying inflation; it too has its faults, not least the apparent arbitrariness of exclusion. But what it does suggest is that forecasters should not just rely on their preferred definitions of variables. In terms of econometric work, it would seem to be important not just to use a number of analytic frameworks to motivate empirical work (like mark-up or Phillips curve frameworks), but also to experiment with a number of definitions of the dependent variable.
Another explanation for the falling power of inflation equations reported by Alex, Ivan and Tim might be that the data on unit labour costs and import prices may not be fully capturing the reality; data are, after all, just constructs, and not the reality itself. The results in the paper show a big shift in homogeneity over the past decade: the joint trends in unit labour costs and import prices grow faster than the trend in consumer prices in the 1980s and then substantially less than the trend in consumer prices in the 1990s.
The data might be a problem in a number of ways.[4] The unit labour cost measure used in the estimation is the economy-wide series, but in the mark-up model it is supposed to be non-traded unit labour costs. It is possible that productivity growth has shifted up, or wages growth has shifted down a notch in the traded sector relative to the non-traded sector over the past decade. This would mean that the cost series used in the econometric work will have been progressively underestimating actual non-traded unit labour costs and causing instability in the parameter estimates. The authors are aware of this issue and accordingly make an adjustment to the import-price measure (as described in their Appendix A). While for estimation purposes this is equivalent to making the adjustment to unit labour costs, it is perhaps not as appealing intuitively.
There are also complications with the measurement of import prices. The growth in ICT imports and greater flexibility in production chains mean that it is harder to accurately identify quality changes in imported goods; to the extent that these are not properly reflected in the import price statistic, there is scope for the statistic to diverge from what it is meant to capture.
These data problems are relevant to the measurement of pass-through as well. In a competitive and much more flexible corporate environment, importers in Australia can respond to movements in the Australian dollar by changing the quality of the goods they sell. To preserve margins as much as possible, for example, clothing retailers shift between single- and double-stitched shirts, electronics firms change the disc-stacking capacity in their CD players, and car retailers shift the airbag, air conditioning, paint and rust-proofing standards for each model.[5] These changes in the quality of the good represent hedonic price changes, but they can be hard to identify and track and so are only incompletely captured in the statistics.
The ability of firms to respond to exchange rate changes by altering the quality and cost of the good rather than shifting the final price of the good has probably increased over the past decade or so. This is likely given the sharp rise in import penetration, the rapid fragmentation of the production chain, the greater frugality in holding stocks, and strengthening links between retailing and manufacturing groups. Pass-through is still occurring, but the form it takes is different and may have become more so. The decline in pass-through in these equations may be, in part, due to these structural and market changes in the economy. The upshot is clear: we have to check that the statistics are measuring the reality.
The results in the paper suggest that inflation in the past decade is best modelled by a constant and the output gap. I think that it would be incorrect for readers of the paper to infer that drivers like unit labour costs or the exchange rate are no longer relevant to the inflation process. (I should emphasise that the authors don't fall into this trap themselves.) Technical problems with inflation forecasting and statistics should not mean that we throw out the theoretical frameworks of inflation underpinning the empirical work (in this case, either the mark-up model or the Phillips curve model). A striking feature of Figure 6 in the paper is just how benign growth in nominal unit labour costs has been, which is in turn due to stable inflation, high productivity growth, a stable economy, and increased competition and contestability in domestic goods, services and labour markets. This can't be taken for granted.
And it has certainly been easier for firms to absorb changes in costs due to exchange rate movements, or perhaps to smooth price adjustment over a longer time period, when overall profitability in the economy has been high and even rising modestly, as it has been for the corporate sector over the past decade. While we don't know the counterfactual, exchange rate pass-through may not have slowed (as much) if profit margins had been squeezed from the mid 1990s. (I wonder whether scaling pass-through by a measure of the strength of profits would add anything to this analysis?)
The horizon for monetary policy
I would like to explore a broader monetary policy issue on which the analysis in the paper by Alex, Ivan and Tim may have some bearing. That is the desirable forecast horizon for setting monetary policy. The rule of thumb that I use from empirical analysis of Australian monetary policy is that the most efficient forecast horizon for Australia is basically one year ahead. This is based on two bits of technical work.
In 1998, Luci Ellis and I used the Bank's system of forecasting equations for inflation, output, the real exchange rate, import prices and wages to ask what sets of weights in a forward-looking Taylor-type rule produce the lowest combination of variability in inflation and variability in output, given the variance-covariance matrix of shocks in these equations.[6] Taking account of feedback loops, we also looked at which forecast horizon produces the most efficient of these policy frontiers. We found that four-quarter-ahead forecasts performed best. Given the lags in the transmission of shocks through the economy, a policy horizon of less than four quarters is inefficient because it would ignore valuable current information about the likely course of the economy. And basing policy on forecasts beyond four quarters was less efficient because forecast errors became bigger the longer the forecast profile; if policy looks too far into the future, it risks responding to phantoms.
In 2002, James Gilbert and I fitted a variety of forward-looking Taylor-type rules (including real-time data estimates of the output gap), and we found that the policy interest rate in Australia in recent decades is best explained as being set on the basis of the four-quarter-ahead inflation forecast, among other things.[7] Given how well monetary policy has been set in the past decade, we took this as an indication that the four-quarter-ahead rule works very well. This profile is also similar to the fitted 12-month forward-looking interest rate rules for the G7 economies estimated by Clarida, Galí and Gertler (1998).
This may be technical work but it makes intuitive sense. Given what we know about what is happening now in the economy, most forecasters are generally more comfortable in saying what they think will happen over the coming 12 or possibly 18 months than over the next 2, 3 or 4 years. Technical analysis confirms the gut view. While there is an obvious appeal in policy-makers thinking carefully about the economic process beyond the standard one-to-two year forecast period, the inherent limitations of forecasting suggest that it is hard to operationalise an extension of the policy horizon.
The paper by Alex, Ivan and Tim highlights the structural instability in inflation equations, which makes it harder to use the inflation equations as tools for forecasting. Their claim is that the speed of pass-through has changed. But the impulse responses do not suggest that the lags themselves have changed all that much; the location of the peaks and the rates of decay are pretty similar across sample periods. This suggests that we may have to conditionally wind back the effect we expect exchange rate movements to have on consumer price inflation (at least when profits are strong). But it does not change the working rule of thumb that the efficient forecast profile for monetary policy is about a year ahead.
Final comment
Let me sum up. This paper is useful in a number of ways.
It provides some detailed analysis on measures of underlying inflation. These measures are now less important in the public debate about monetary policy, but they remain necessary tools in the engine room of economic analysis. It is valuable to put this work in the public domain; it may be a bit too esoteric for the average punter, but it is especially helpful to other economists.
The paper also presents evidence on the reduction in exchange rate pass-through to consumer price inflation. I don't think we really understand this. How different would the outcome have been, for example, if profits had not been as strong as they have been? How well are the statistics capturing what is going on in the economy? How dependent are the results on the particular measure of underlying inflation used, especially a measure which may remove systematic economic information? The paper is honest in showing how hard econometric analysis can be in a policy environment. One tool in the forecaster's kit might not be working so well at the moment. But it is not the end of the world. We do have better measures of expectations than we had a decade ago. It does not shake views on other aspects of policy analysis, such as the preferred forecast horizon. And nor does it necessarily follow that the analytical frameworks which underpin this particular technical work have failed.
I would like to thank the authors for a stimulating paper and the Reserve Bank for the invitation to discuss the paper. Having spent a number of years in the mid 1990s modelling inflation at the Bank, I feel a welcome sense of coming home and nostalgia in discussing these issues today.
Footnotes
Principal Adviser (Macroeconomic), The Australian Treasury, and Professor, Asia Pacific School of Economics and Government, Australian National University. I am grateful for comments from Laurie Brown, David Gruen, Adrian Pagan, Tony Richards, Nick Stoney and Martin Parkinson. Comments welcome to gdebrouwer@treasury.gov.au. The views expressed here are those of the author alone and should not be represented as the views of the Australian Treasury, the Australian Government, or the Australian National University. [1]
In these estimations, a GST dummy is included for the four quarters starting September 2000. The dummy enters in both the long run and short run. [2]
I am grateful to Laurie Brown and Nick Stoney for this analysis. [3]
I am grateful to David Gruen for discussions on this. [4]
I am grateful to Nick Stoney for these examples which have come from Treasury's business liaison program. [5]
See de Brouwer and Ellis (1998). [6]
See de Brouwer and Gilbert (2002). [7]
References
Clarida R, J Galí and M Gertler (1998), ‘Monetary policy rules in practice: some international evidence’, European Economic Review, 42(6), pp 1033–1067.
de Brouwer GJ and L Ellis (1998), ‘Forward-looking behaviour and credibility: some evidence and implications for policy’, Reserve Bank of Australia Research Discussion Paper No 9803.
de Brouwer GJ and N Ericsson (1998), ‘Modelling inflation in Australia’, Journal of Business and Economic Statistics, 16(4), pp 433–449.
de Brouwer GJ and J Gilbert (2002), ‘Monetary policy reaction functions in Australia’, paper available at <http://apseg.anu.edu.au/staff/gdebrouwer.php>.
General Discussion
The discussion of the two papers ranged over a variety of issues, a number of which were common to both. Considerable attention was given to the impact of administered prices – such as those for education, child care, heath care and pharmaceuticals – on the CPI. One participant noted that, until the last few years, the traditional method of forecasting inflation using unit labour costs and import prices (as discussed in the Heath, Roberts and Bulman paper) had worked reasonably well. In the last couple of years, however, this approach has led to a considerable underprediction of inflation. The difference could be explained by administered prices, which comprise 14 per cent of the CPI by weight and have recently been growing at 5–6 per cent a year. It was suggested that this might better explain the low inflation implied by the Treasury underlying measure of inflation relative to other underlying measures over the past year or so. As a number of participants noted, this phenomenon has wider implications: monetary policy has to press harder on non-administered prices to maintain inflation within the target band; it has become more difficulty to estimate inflation using a mark-up model; and, as administered prices are changed infrequently, say every four quarters, trimmed measures of the CPI calculated at a greater frequency will tend to be biased downwards.
Following Kent's comments, there was some discussion of the implications of possible biases in the CPI. One participant agreed that, while it was technically true that inflation mismeasurement did not pose problems for the monetary policy process, it was important for central bankers to be involved with CPI formulation and measurement issues. Another participant questioned whether it mattered for the central bank if the magnitude of the measurement bias was unknown, but thought to be relatively stable. In this respect it was noted that greater quality adjustment would potentially lead to greater instability in the measurement bias. One participant suggested that in addition to the need for a low bias in order to gain wide community acceptance of the measure of inflation that the central bank is targeting, accurate measurement of prices is important for contracts that include indexation clauses, and for the measurement of real income.
In terms of other measurement issues, one participant noted that the use of expenditure weights in the CPI meant that the CPI was likely to better represent wealthier households, who have a higher absolute value of expenditure. To overcome this, it was possible to construct ‘democratic’ CPIs, using expenditure weights for individual households (from household expenditure surveys), rather than the average of all households. Encouragingly, preliminary work at the Reserve Bank suggested that the average CPI measured across households is roughly similar to the expenditure-weighted CPI, although there was wide variation in the inflation experience across households. The use of democratic CPIs may help to shed light on experiences such as the introduction of euro notes and coins, when segments of the population thought that inflation was quite high. This may have reflected relative expenditure patterns, with some people not benefiting by much from the prices that had come down, but were focusing instead on items they purchased frequently whose prices had increased.
There was also considerable discussion of the slowdown in import price pass-through in recent years. There was general agreement that this was a common phenomenon across the industrialised world and thus seems to be a feature of low and stable inflation, independent of any variation in the structural characteristics of countries, including economic size. The econometric difficulties of measuring changes in pass-through were covered at some length. A number of participants accepted that the significant fall in inflation variability over the past decade or so made estimating the relationships in an inflation equation considerably more problematic. A number of participants also noted that with the fall in pass-through, the unit labour costs component of the inflation equation assumed greater importance. One participant contended that the estimation problems highlighted by the Heath et al paper were not encountered if the equation was estimated before and after the float of the Australian dollar in 1983. More specifically, the import price pass-through coefficient had changed between these two periods, but in the post-float period pass-through had not changed between the period of high inflation and the period of low inflation. These results further illustrated the sensitivity of the estimate to the choice of sample period. Finally, one participant noted that, while a lot of work had been undertaken examining the statistical properties of the dependent variable in the inflation equation, there had been relatively limited work trying to better understand the independent variables – most notably unit labour costs. Better measures here may lead to an improved mark-up model.