RBA Annual Conference – 1998 Prospects for Output and Employment Growth with Steady Inflation Mardi Dungey and John Pitchford[*]
1. Introduction
Monetary policy affects both real variables, such as employment, unemployment and output, and nominal variables, such as nominal interest and inflation rates. For close to a decade, the principal focus of monetary policy has been on inflation. During a recession, or when one appears imminent, the state of real variables such as GDP growth has been a paramount consideration, but at other times, inflation control has been the major objective. We argue that this concentration on inflation has not been misplaced, indeed we suggest that it should be more detailed than it has been. Nevertheless, we see a critical role for monetary policy in reducing unemployment that has not been explicit in some standard approaches to inflation. While we spend a considerable time looking at inflation issues, the objective in doing so is to substantiate the point that adequate management of inflation will leave more scope for real growth and hence for lowering unemployment.
Despite the difficulty of quantifying the costs of moderate inflation, its control is important because in certain circumstances, low inflation can lead to accelerating prices and so to high inflation which does have high costs. Further, bringing inflation down once it has begun to rise has often involved a recession that has been costly in terms of foregone output and lasting unemployment, so that it is better not to have let it rise in the first place.
Macroeconomic policy can reduce unemployment both by ameliorating recessions, and by achieving growth at a rate consistent with steady inflation. The investigation of the latter concept is central to this paper and it will be called the steady inflation rate of growth or SIRG.[1] The conventional method of analysing inflation has been to examine how the divergence between actual and expected inflation is related to unemployment. The resulting estimate of the NAIRU, or non-accelerating inflation rate of unemployment, would then provide macroeconomic policy with the aim of ultimately achieving that unemployment rate so as to establish equilibrium with steady inflation. However, there is strong evidence that the NAIRU has been highly variable in many countries, with the possible exception of the United States.[2] For the NAIRU to be a reliable concept for guiding macro policy the determinants of how it shifts would need to be well established empirically and the results, particularly for Australia, do not bear this out. Moreover, the NAIRU is a labour market concept relating expected real wage movements to labour market disequilibrium, whereas inflation refers to prices in goods markets.
Hence we have chosen to work with explanations of the rate of price change which link it directly to the state of excess demand in product markets. The consequent empirical results, both for Australia and other countries, lead us to regard the SIRG as a way of characterising the inflation process that is superior to that embodied in the NAIRU. Also, it gives a direct estimate of the growth rate consistent with steady inflation. In combination with estimates of labour demand and supply elasticities, the SIRG facilitates discussion of scenarios of output, wages, employment and unemployment consistent with the objective of steady inflation.
Section 2 of the paper provides a brief outline of the model that underlies our analysis. Section 3 deals with the theoretical and empirical analysis of the connection between inflation and growth, and hence with estimates of the SIRG. We also make the point that movements in the inflation rate attributable to real exchange rate fluctuations need to be investigated separately from inflation arising from domestic excess demand. Our conclusion is that monetary policy should also make this distinction.
There is no guarantee that the growth rate compatible with steady inflation will also ensure that unemployment can fall. The answer to this question partly depends on knowledge of particular labour demand and supply elasticities, and on knowing how conditions in the labour market and wage-setting institutions affect real wages and employment. But to know this is to know how the labour-market side of the Phillips curve/NAIRU system works. Instead, in Sections 4 and 5 we follow the conventional approach and use our own and others' estimates of labour market elasticities to provide scenarios of how various growth rates, including the SIRG, and real wage movements could affect unemployment. In Section 5 we argue that deriving the impact of growth on unemployment requires consideration of short-run, as well as long-run, employment elasticities. The policy conclusions of the paper are set out in Section 5 where the implications of our approach to, and estimates of, the sources of inflation are used to derive principles for monetary management and to look further at unemployment prospects. Some concluding comments are given in Section 6.
2. A Macroeconomic Model of Unemployment and Inflation
The view of the economy behind our paper is the constrained equilibrium class of models, such as those developed by Barro and Grossman (1976), Muellbauer and Portes (1978) and Malinvaud (1977). These systems deal systematically with disequilibrium in labour and product markets. That is, when there is excess demand for goods, actual output is constrained to equal supply, and when excess supply prevails, it equals demand. Prices for domestically produced goods adjust to excess demand and supply, and to expectations of inflation. If the practice is followed of using last period inflation as an estimate of expected inflation, it is readily seen that excess demand causes inflation to rise. Similar structures are assumed for the labour market, with the expected real wage adjusting to disequilibrium.
Thus we focus on conditions in the markets for goods and services as the generator of inflation for those goods produced domestically that are not in close competition with imports or exports. Goods consumed domestically consist of such goods plus some traded goods, mainly imports in Australia's case, so that the consumer price inflation rate will depend on both the state of the goods market (excess demand), and the rate of inflation of import prices. Notice that a real wage adjustment equation, with features in common with the standard approach to inflation, will still exist. It will determine real wage movements and hence be one factor in the determination of unemployment.
Aggregate demand for domestic output is taken to be of the IS form, depending on real income at home and abroad, fiscal variables, the real interest rate, the real exchange rate and the terms of trade. However, unlike the usual IS approach, the goods market will not clear except in equilibrium. Money demand and supply are of the standard LM form, with the central bank setting the nominal interest rate in accordance with its objectives.
The supply of output, depending on inputs of productive factors and technology, will equal aggregate demand only in equilibrium. In disequilibrium, actual output will be adjusted toward the short side of the market both by accumulating (or running down) stocks and by adapting the intensity with which inputs are used. Thus firms can vary hours of work of factors above or below normal levels which define potential output. The gap between actual and potential output is one measure of excess demand that drives domestic goods price inflation. The foreign currency prices of most of Australia's traded goods will be determined in world markets, so their domestic currency prices will also reflect exchange rate movements.
The demand for labour hours LD is given by its marginal product, and can be expressed in a form in which it depends on the level of output, the hourly real wage paid and the rate of labour-augmenting technical change. Because of problems associated with hysteresis, labour supply is not a straightforward concept. For some purposes it is the supply of those working plus those seeking work, as measured by the labour force statistics. This is denoted by LC in Figure 1. Some of those seeking work are so lacking (or perceived to be lacking by employers) in required work skills that they have either lost (because of their unemployment history) or never acquired, that their supply for these and other reasons does not put downward pressure on the real wage.[3] They are not part of ‘effective labour supply’ which is given by LE.[4] Hence, while we observe points on LC and LD, LE can only be estimated indirectly out of equilibrium. When the labour market is in equilibrium at the wage that equates LD and LC, the difference between LE and LC measures the natural rate of unemployment.
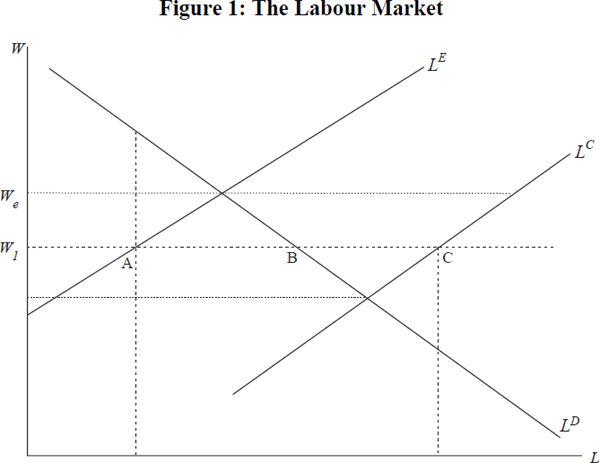
With the wage W1 there is effective excess demand for labour of AB which will cause wages to rise despite the existence of unemployment as measured by BC = LC–LD. Changes in output and population, as well as technical change and the history of unemployment will shift the functions in Figure 1. Together with changes in real wages, these shifts will determine the path of employment and unemployment. A rightward movement in labour demand is one of the factors which might help create favourable labour market conditions that will result in some transfer of labour into the effective labour supply. Rising real wages can have a similar effect if they create a gap between reservation earnings, such as unemployment benefits, and wages sufficient to induce movement into the effective workforce. Real wages will normally adjust to eventually create labour market equilibrium, as represented by equality between LD and LE. However, unexpected price movements and non-market wage-setting will cause real wages to move away from equilibrium levels.
Notice that the model is basically symmetrical in its treatment of the goods and labour markets. Actual supplies are constrained by the short side of each market and disequilibrium in each market drives the relevant relative ‘price’ adjustment. There is no need for a mark-up pricing relationship, the definitional association between prices and the costs of factor inputs determining ex post profits as a residual. Inflation is generated in the product markets.
3. Inflation, Growth and Import Prices
The prices of domestically produced goods P and of imports M enter into the index of prices of local consumption with constant geometric weights a and (1–a).[5] Lower case is used to represent the proportional rate of change in a variable, so that the inflation rate π of the index is:

Domestic goods prices are supposed to adjust to excess demand x according to
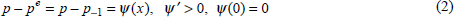
The expected price change pe is taken to be determined by the change in the previous period.[6] Combining Equations (1) and (2):

We estimate the price equation in the form in Equation (3).[7]
Two issues must be faced before this can be done. The first arises because Australia floated in 1983:Q4 and previously had pegged or heavily managed its exchange rate. Secondly, excess demand in the goods market is not directly observable, though there are a number of measures that are used to approximate it. Consider the exchange rate question. Pegging to a single currency or a basket means that fluctuations in those prices determined on world markets are liable to be transmitted to the local economy in a fairly direct manner. Further, it will be difficult to prevent foreign monetary expansion resulting in domestic monetary expansion, except by the process of raising interest rates and reducing activity to such an extent that financial capital inflow is discouraged. By contrast, with a floating rate, domestic monetary policy can be independent of foreign monetary conditions. It could be that the exchange rate system may approximate the theoretical notion of ‘exchange rate insulation’ and ensure that domestic inflation is independent of an average of movements in the foreign-currency prices of traded goods.[8] Hence, it is preferable to examine the generation of inflation either for a pegged or a floating rate system, but not across both.[9] For these reasons we have concentrated our empirical analysis on the period of floating from 1983:Q4.
There are a number of observable variables that could proxy for excess demand in the product market, the gap between actual and potential output being one of the more popular. Potential output is also not directly measured and is often taken to be some average of output levels. One difficulty about this is to know over what period and phase of cycles to take the average, though different approaches could be accepted or rejected on the basis of their empirical performance. Instead we have chosen to work with the rate of economic growth as the excess-demand proxy.[10] Apart from the empirical results this yields, there are some good theoretical reasons for this choice. We have also estimated an inflation equation using an output gap approach. The results, although similar, were not superior to those with growth as the proxy.
The most compelling reason for relating inflation to real growth is that the growth of the labour force and capital stock, in conjunction with technical change, will at any time determine an underlying growth rate of ‘potential’ output. In the absence of large exogenous shocks and cycles, this growth rate would probably remain relatively constant. If the supply potential from this growth were matched by demand growth at the same rate, there would not be pressure for prices to rise. When the growth of demand exceeds that of supply, price signals will be required so that the intensity of use of factors can be increased.[11]
There are arithmetical relationships between the growth rate of actual and potential output and the divergence of output from some average level. To see this, define the growth rate g and excess demand x as:

where 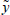 is potential and y
actual output. Then:
is potential and y
actual output. Then:
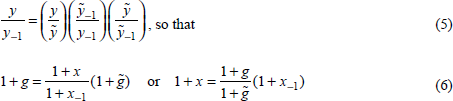
The growth rate is positively related to this period's excess demand and the
growth rate of potential output 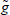 and negatively related
to last period's excess demand. Further, rewriting Equation (6) for time
period −1, and by repeated substitution into Equation (6), taking logs,
and using the approximation ln(1+z) ≅ z, this
relation can be written:
and negatively related
to last period's excess demand. Further, rewriting Equation (6) for time
period −1, and by repeated substitution into Equation (6), taking logs,
and using the approximation ln(1+z) ≅ z, this
relation can be written:

where µ(g) is the mean of g−t in the interval [−T, −1]. If these means are sufficiently close to the growth rate of potential output, g will be a good approximation to excess demand plus a constant.[12] Figure 2 shows the behaviour of g.
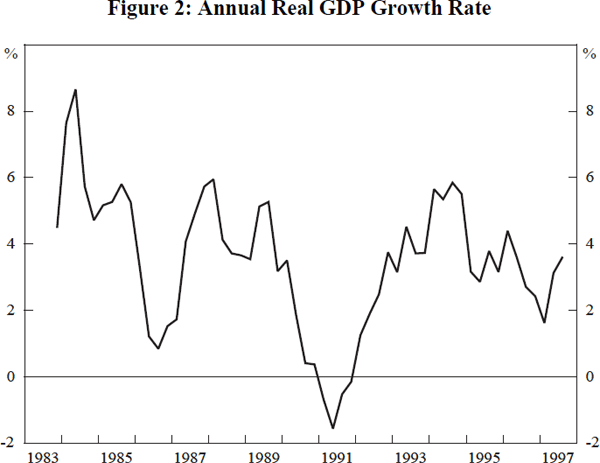
Another check can be made of our choice of growth as an excess demand proxy by regressing a measure of the output gap on growth. Some details are given in Appendix C from which it can be seen that the two series are highly correlated.
Growth can also proxy for adjustment costs that are dependent on changes in the level of, and/or growth rate of, output. For instance, suppose the economy is just leaving a recession, but output is still well below levels that would denote a boom. Although the economy is relatively depressed, a high growth rate at this time could nevertheless still produce price rises. Despite unemployed resources, adjustment costs could mean that it might be difficult to bring them into production in the short run without price signals.
Equation (8) gives the form of the encompassing equation for our general-to-specific approach. It was estimated by OLS using quarterly data. Using the standard ADF tests we accepted that the inflation rate, growth rate and import price inflation were I(1) in nature. The errors in Equation (8) were indistinguishable from white noise:[13]
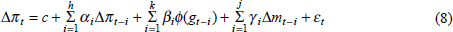
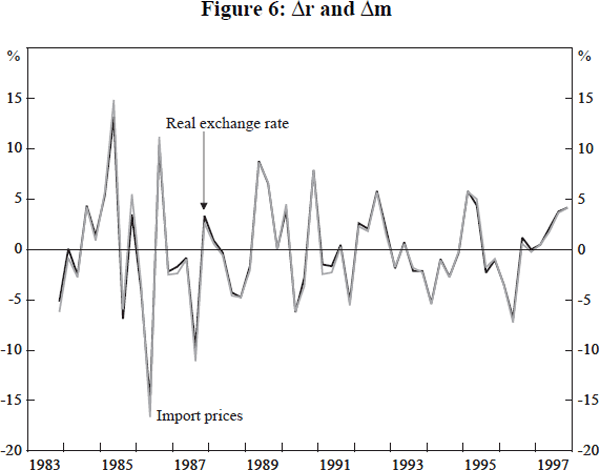
Here, π is the annual Treasury underlying consumer price inflation rate, g is the annual percentage growth rate in real GDP(A), φ is some function of g, and m is import price inflation. Full data definitions and sources are given in Appendix A. Data on the independent variables are illustrated in Figures 2 and 6.
Lagged values of the dependent variable were included to account for a potentially dynamic adjustment process. Estimation of Equation (8) with φ(.) as a linear function met all tests except the RESET test of functional form, leading us to consider non-linearities in the relationship. The introduction of an increasing inflationary response to incremental increases in excess-demand pressure produced a preferred form of the equation as per Equation (9) for the post-float period. The variable gs refers to the squared growth rate in real output, with the sign of the growth rate reassigned, so that, for instance, if the annual growth rate in one quarter was −2 per cent then gs for that quarter would be −4 per cent. Further details are available in Pitchford and Dungey (1998).
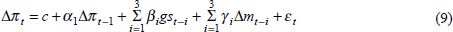
In the final analysis we could not reject the hypothesis that the coefficients on the first and second lags of gs were of equal value and opposite sign. After imposing this as a restriction, the change in the inflation rate was related positively and equally to both the change in the ‘square’ of the growth rate (lagged once) and the ‘square’ of the growth rate itself (lagged 3 times).[14] The estimated equation is shown in Equation (10), with standard errors given in parentheses. Recursive estimation indicated that these parameter estimates were stable over the estimation period.
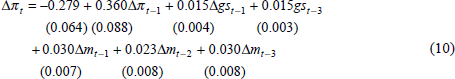
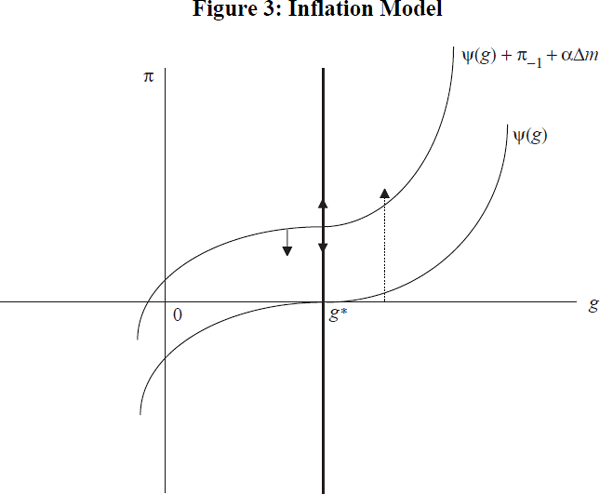
The lagged value of the inflation rate was significant, suggesting that not all of the adjustment of the domestic inflation rate implied by Equation (8) is completed in each period.[15] The functional form relating growth to inflation change is illustrated in Figure 3 where ψ(g) = φ(g) − g* and ψ(g*) = 0.
3.1 The influence of growth on inflation
The models enable an estimate to be made of the growth rate of GDP compatible with steady inflation, or SIRG. If both the index of inflation and the rate of import price inflation are constant, then from Equation (8),

Calculating the SIRG g* from gs*, for the data period of the float from December 1983 it is 4.37 per cent per annum.
Figure 3 illustrates how the system works. Suppose, initially, that Δm = 0. The function ψ(g) represents inflation outcomes when the expected inflation rate is zero. Plotted against the inflation rate, it is positively sloped except at g* where it intersects the g-axis. If growth is at g*, the inflation rate can lie anywhere along the vertical axis through g*. If g rises above g*, the inflation rate will rise and this can be reduced by a period of growth below the SIRG. The story is analogous to that often given for the NAIRU, though it will be seen to be different from the standard NAIRU case when non-steady import price inflation is considered in the next section.
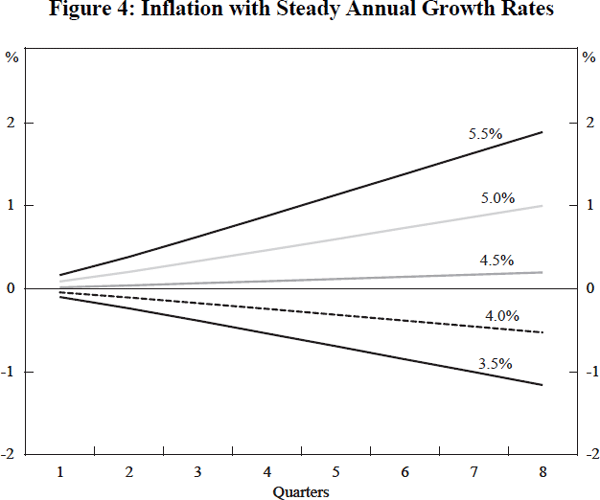
To appreciate the magnitude of the effect of growth on inflation implied by the coefficients given in Equation (10), consider the consequences of a sustained rise or fall in g when the system has been at the SIRG for a long period, illustrated in Figure 4. Starting from a steady state with zero inflation, and then setting a steady GDP growth rate of 5.5 per cent per annum will mean that the system will reach about 1 per cent annual inflation after one year, and 2 per cent after two years. By comparison, with a 5 per cent real growth rate, inflation will take twice as long to reach 1 per cent per annum. After two years, with 4 per cent GDP growth, annual deflation of about 0.5 per cent per annum will have been attained. All this assumes that import prices are not contributing to inflation.
3.2 Import prices
Growth and hence employment are affected by policy toward inflation. We have shown that a steady inflation rate for domestic goods can be achieved by setting the growth rate at the SIRG. On the other hand, import prices fluctuate considerably (Figure 6) so that stabilising the overall inflation rate could require large oscillations in growth and hence in unemployment. Here we argue that it is critical to distinguish between, and adopt different policies toward, these two sources of inflation.
According to the ‘law of one price’, a behavioural relationship, arbitrage will ensure that:

where H is the nominal exchange rate (the reciprocal of the TWI), M* the foreign currency price of imports, and M the price in domestic currency. For the post-float period, a simple regression of m on h yields a correlation coefficient of 84 per cent and of h on the inflation rate of the price index (π), a correlation coefficient of 6.3 per cent. Domestic-currency import price inflation is closely associated with nominal exchange rate variations. But nominal exchange rate variations are much larger than those in the domestic inflation rate. Hence, there is a priori evidence that domestic-currency import prices are more closely related to exchange rate changes than to domestic conditions, and domestic inflation and exchange rate movements are quite dissimilar.[16]
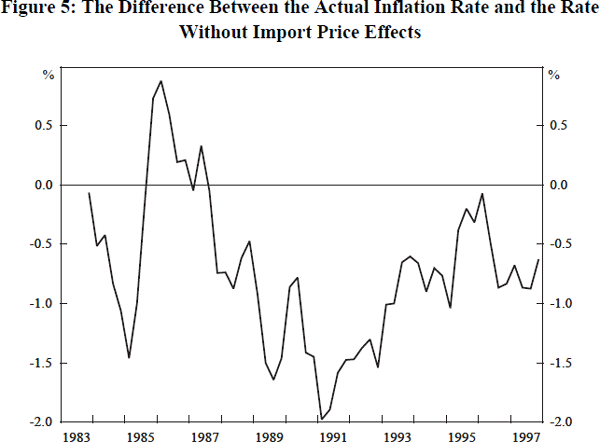
Import prices enter into the results in the way predicted by Equation (3) with lags of one, two and three periods. One way of appreciating their influence is to ask what inflation would have been if import prices had contributed to inflation to the same extent as domestic goods prices. This can be determined by substituting π for m in Equation (10) and calculating the consequent inflation from a base date, December 1983. The results are summarised in Figure 5 from which it can be seen that import price inflation held down the overall inflation rate by between one and two percentage points since 1987. Depreciation in the mid 1980s added to inflation, but from about 1987, the contribution of import prices has been steadily negative. Anti-inflation policy has benefited considerably from these import price movements.
If import price inflation rises, the curve ψ(g) rises (Figure 3), but it keeps moving up only if import price inflation continues to increase. It is important to note that this is different from the case of growth, where if g rises above g* and stays there, domestic goods inflation will perpetually rise. A period of falling import price inflation will cause the curve to fall.[17]
Another way of expressing these issues is in terms of the real exchange rate R. For present purposes its definition must involve the price of imports.[18] Hence:

Rearranging Equation (9), the inflation equation can be expressed in terms of past increments in inflation, growth terms and changes in the real exchange rate:
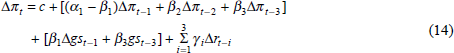
Movements in Δr and Δm are illustrated in Figure 6. The difference Δm − Δr is the change in the inflation rate. Rises follow falls in Δm with cycles lasting about two to three years. It is clear that most of the variation of Δm is accounted for by the variation associated with the real exchange rate. An implication is that steady growth at the SIRG would mean that the overall inflation rate drifts up and down with fluctuations in import price inflation, without causing a rise in domestically generated inflation. In addition, when import inflation is decelerating, growth could exceed the SIRG without causing overall inflation to rise. Notice that this result stems from the generation of import price fluctuations by the movements in the real exchange rate, a real variable. Hence, it holds irrespective of the way in which domestic goods prices are thought to be determined. The policy implications of these issues are considered in Section 5.
4. The Labour Market and Growth
Estimated relationships between labour demand and output growth allow assessment of the potential for employment growth. We review various estimates of the relevant elasticities and consider their implications for employment and wage growth here and in Section 5.3.
The structure of the labour market has changed since the 1960s. Employment has been increasingly part-time, women make up a larger segment of the labour force and working hours have altered. Despite this, employment remains dominated by full-time employees (74 per cent in 1997) and the majority of the unemployed are seeking full-time work (78 per cent in 1997). Consequently, we consider total employment and unemployment to be appropriate measures for macroeconomic analysis.
Labour demand is normally derived using a production function to relate real wages to the marginal product of labour.[19] Consider an aggregate CES production function relating capital (K) and labour (N) in the production of output Y:

where β/α is the degree of returns to scale. The elasticity of substitution is found from:
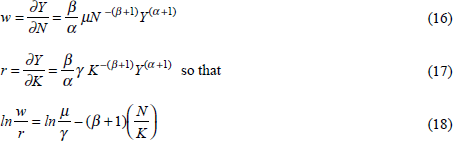
It follows that the elasticity of substitution σ is 1/(1+β).
Equation (18) is a labour demand function relating N to time (through μ (t)), w and Y. Writing it in logarithmic form:
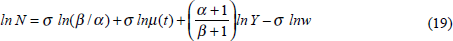
which in the constant returns to scale case reduces to:

Supposing 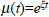 , in the general case:
, in the general case:
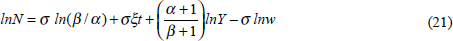
The (semi-) elasticities with respect to time, output and real wages, respectively,
are σm, (α+1)/(β +1), and σ. In the constant
returns to scale case they are 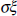 , 1, and σ, and
the constant is zero.
, 1, and σ, and
the constant is zero.
Various estimations of this form of labour demand equations have been carried out for Australian data and internationally. There are many disadvantages to such a system, the most striking being the identification problem. However, in the spirit of Hamermesh (1993) we consider that naive labour demand equations of this type have some merit as a benchmark for more sophisticated analysis.[20]
In Dungey and Pitchford (1998) we estimate a naive labour demand curve in error-correction model (ecm) form for a number of market segments and measures of labour and real wages. Here we report only the results of demand for labour in persons. The use of employed persons, rather than hours, raises the question of potential substitution between employees and working hours. Firms may choose to pay more for extra hours from existing employees rather than hire more bodies (Hamermesh 1993), and they may choose to hire extra persons on a part-time basis. The Australian labour market has changed over the past two decades, in particular it has become increasingly flexible. One consequence is that additional persons employed may not accurately reflect changes in the hours of labour demanded. In an attempt to account for the changing hours of work, we augment the traditional labour demand equation with an hours-worked variable as per the TRYM model of the Australian economy (Commonwealth Treasury 1996). The form of the estimated equation in Dungey and Pitchford (1998) for all employees over the period 1984:Q4 to 1997:Q1 is:
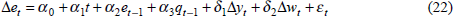
where e is total employment, t is a trend variable and q is a vector of independent variables comprising real output y, given by GDP(A); real wages w, represented by real earnings; and average weekly hours, hr. ε is a random error term. The variables are in logarithmic form and full data descriptions and sources are contained in Appendix A. Further details regarding the estimation of Equation (22) are contained in Appendix B. The following results were obtained:
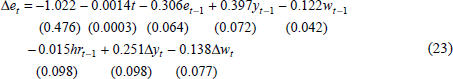
In both our estimates and the existing Australian empirical literature, the form of the long-run relationship in the estimating equations can be characterised as in Equation (24):

where z is a vector of independent variables and η is the corresponding vector of coefficients.
In this section we are interested in the long-run elasticity parameters γ2 and γ3 and the technological change parameter γ1. Our output elasticity is a little higher and wage elasticity somewhat lower than the findings of earlier researchers, but are consistent with those of Debelle and Vickery (1998). As they note, part of this effect is due to the choice of data and time period.
Estimation of Equation (22) over a longer time period suggests similar wage elasticities, and the standard Chow tests do not indicate breaks in the relationship. However, recursive estimations indicate that the regressions had difficulty in fitting the data in the early 1980s, in a period where employment growth continued despite high wage growth (Gregory 1986; Crosby and Olekalns 1998) suggesting there is a case for distinguishing the recent labour market experience from earlier evidence. Russell and Tease (1991) estimate the long-run wage elasticity at 0.67 for full-time male employees using real unit labour costs as the measure of wages for the period 1969–87.[21] The TRYM model obtains an elasticity of substitution of 0.78 after making adjustment for the impact of vacancies over the business cycle for 1971 to 1995 (without this adjustment the reported wage elasticity is calculated at −0.32). Table 1 gives the values of γi from the TRYM model (Commonwealth Treasury 1996), Russell and Tease (1991) and our estimates.
| Study | Technical change (γ1) | Output elasticity (γ2) | Wage elasticity (γ3) |
|---|---|---|---|
| Dungey and Pitchford | −0.005 | 1.30 | −0.40 |
| TRYM | −0.008 | 0.91 | −0.79 |
| Russell and Tease | −0.0005 | 0.67 | −0.61 |
Under the assumption of no change in the zt variables, the relationship in Equation (25) enables consideration of consistent scenarios of employment, output and real wages growth using long run elasticities:

Using the parameters in Table 1, we produce a set of ‘scenario’ charts to illustrate the consequences of long-run elasticities. Consider first the naive estimates from Dungey and Pitchford.
Figure 7 shows bands of real wage growth consistent with output and employment growth in the economy. According to the naive parameters, if real output in the economy is growing at 3.5 per cent, then employment growth of between 0.5 per cent and 1 per cent per annum is consistent with real wage growth in the 4–6 per cent band.[22] As the real output growth rate increases and the rate of employment growth falls (a move right and down in the graph) the consistent real wage growth rate rises. At higher (lower) output growth and lower (higher) employment growth, the consistent real wage growth rises (falls).
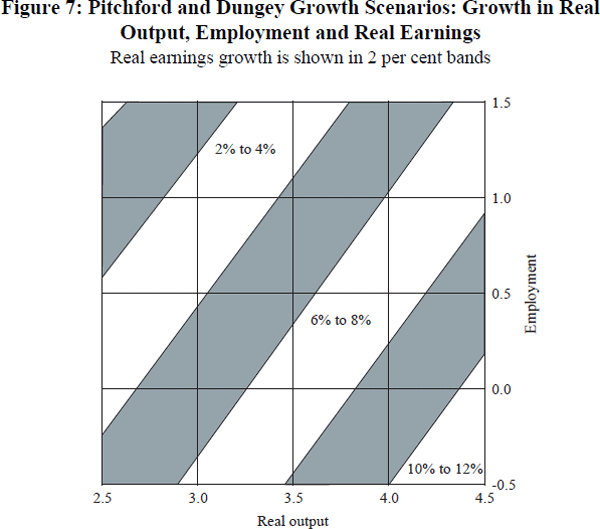
For the parameter estimates from TRYM and taking the case of 3.5 per cent real output growth, falling employment growth is associated with positive real wage growth (Figure 8). For the Russell and Tease estimates, 3.5 per cent output growth is consistent with positive employment growth when real wage growth is less than 4 per cent per annum. The Russell and Tease scenarios (not shown here) indicate higher real wage growth rates consistent with falling employment (through growth below the SIRG) than do the TRYM model scenarios, but lower real wage growth than our estimates.
It should be borne in mind that these elasticities are ‘long run’ constructs so that their use to illustrate short-run scenarios may be inappropriate. In Section 5 we use the adjustment equation from which these elasticities are derived, in conjunction with further assumptions about wage and GDP growth rates, to construct several prospects for unemployment.
5. Policy Issues
The results in preceding sections suggest ways of achieving higher growth of employment and output consistent with steady inflation. These are discussed under the headings of sources of inflation, the SIRG, and real wages and unemployment.
5.1 Sources of inflation
Attempting to manage inflation without reference to its source is likely to lead to considerable fluctuations in growth. In particular, inflation arising from domestic excess demand should be distinguished from inflation due to import price movements as they have been shown to have different types of behaviour, a point also made by Stevens (1992). Thus, if the equilibrium growth rate is exceeded, domestic inflation will start to rise. The options will then be either a period of growth below the SIRG or the prospect of the eventual establishment of a permanently higher inflation rate at the SIRG. On the other hand, while rising inflation of imported goods can cause the overall inflation rate to rise, a subsequent fall in this source of inflation will bring the inflation rate down again, without the necessity for departing from the SIRG. Movements in the real exchange rate (defined as the ratio of the import price deflator to the underlying consumer price index), are the major source of fluctuations in this category of inflation (Figure 9). The factors influencing it include monetary and fiscal disturbances, movements in the IS and LM curves, shifts in currency preferences and changes in the terms of trade.
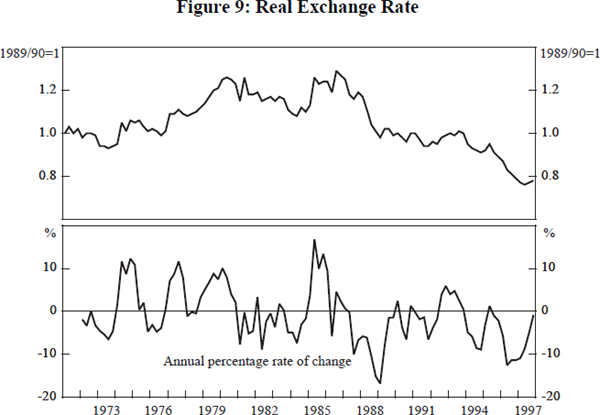
It can be seen from the rate of change part of Figure 9 that the real exchange rate fluctuates widely and regularly. Also the index shows that there have been long periods of appreciation and depreciation, depreciating in the mid 1980s, appreciating in the late 1980s and through 1984 to 1987. How should policy respond to the effects on inflation of such real exchange rate movements? Earlier we noted the benefit that the recent real appreciation provided for inflation control in the 1990s, but what about depreciation? Suppose the economy is at some target positive inflation rate. Real depreciation means that the prices of imports rise relative to those of domestic goods. In order for monetary policy to maintain inflation at a particular rate, GDP growth would be required to fall. In the face of real exchange rate changes there would seem to be a strong case for maintaining the SIRG while letting inflation fluctuate. From Figure 5, it can be seen that the large depreciation in the mid 1980s significantly increased the inflation rate, but subsequently this was more than offset by the large appreciation through to the end of the decade. Real appreciation continued to reduce the pressure on inflation through to 1997.
If a real depreciation is allowed to raise inflation it could also have an effect on nominal and real wages and so on unemployment. Theoretical analysis does not give unambiguous results about the impact of relative price shifts on real wages, the outcome usually depending on factor intensities in different sectors.[23] Leaving this aside, the reaction of the authorities in the case of the mid 1980s depreciation was to attempt to calculate the effects of depreciation on inflation and argue that nominal wages should not be raised by that factor. This seems preferable to reducing real growth. Such policies should be increasingly unnecessary as wages become more market determined.
Although domestic macroeconomic policy can influence the real exchange rate to some extent, it is probably fair to say that very large shifts in interest rates would be needed to offset its changes and that much of its movement due to foreign sources is outside such control. Hence, it would seem undesirable to attempt to control it, unless doing so accorded with some other objective. As a consequence, modest rates of inflation generated by import prices need not give rise to policy responses.
Data on inflation, import prices and GDP are available to policy-makers only after a considerable delay. However, the association between import price inflation and the TWI is sufficiently strong that its quarterly and monthly movements can provide some early indication of the import price component's effect on inflation, which could assist the process of distinguishing the two sources of inflation. This is discussed further in Appendix C.
5.2 The SIRG
Policy toward inflation consists of two parts. The first involves choosing a desired inflation rate, which in Australia takes the form of a target average rate falling in the band of 2–3 per cent per annum. The second is achieving the band, which in a stochastic sense can be thought of as attaining steady inflation at the desired rate. In such an equilibrium, growth would be at the SIRG and inflation could fluctuate with real exchange rate movements.
When the domestic goods component of the inflation rate is rising or falling, some procedure for adjusting interest rates is needed to bring the system to steady inflation. A problem with rules which target only overall inflation is that they do not distinguish between inflation arising from import prices and that originating in domestic goods markets. Following such a rule with respect to the inflation index would lead growth to fluctuate when the real exchange rate fluctuated. Moreover, if there is evidence that suggests the existence of a growth rate consistent with steady inflation in the domestic component, it would seem appropriate to use it. If growth is less (greater) than the SIRG, our analysis suggests that whatever rule operates, growth should be increased (reduced).[24] Further, it would be prudent to watch inflation, both from domestic sources and from import prices and to react to their movements. Another consideration is that because of possible shifts through time, the use of the SIRG to guide policy would need to be handled with care. Of course, this also applies to all policy indicators.
A possibility for a period of growth above the SIRG could arise when the contribution of real exchange rate movements to inflation is negative. This could particularly be the case when a program to reduce unemployment is current. It might be feasible at such times to edge growth up without raising the inflation rate. However, it would then be important to bear in mind that the effect of higher growth on inflation may come with a lag of close to six months, allowing for the delay in data availability. The situation would need to be appraised on the basis of the facts available at the time.
It might be thought that a conservative policy approach to inflation would be to keep growth below the SIRG. However, if this were done, and taking the case of a neutral impact from import prices, the inflation rate will fall. If there is a cycle in growth, inflation will fall on average. Low inflation rates pose a problem for monetary policy because the floor to nominal interest rates may not allow real interest rates to be set low enough to help revive the economy from recession. Hence, some target positive average inflation rate over a cycle will not be met unless growth exceeds the SIRG in a boom as well as falling below it in the trough.
5.3 Real wages, growth and unemployment
Employment elasticity estimates can be used to give an answer to the question of the effect of changes in the non-market component of wages on employment.[25] Instead of addressing this issue, we use the elasticities from Section 4 to examine various possibilities for reducing unemployment through higher growth. To do this it is necessary to make assumptions about the behaviour of real wages and output. Table 2 provides a way of looking at their association through time. Even the period 1972:Q3 to 1983:Q3, which includes the large real wage increases in the seventies and early eighties, did not result in average real wage growth exceeding that of real GDP.
| Mean growth | 1972:Q3 – 1983:Q3 | 1983:Q3 – 1989:Q3 | 1992:Q3 – 1997:Q4 | 1972:Q3 – 1997:Q4 |
|---|---|---|---|---|
| Real GDP | 2.7 | 4.4 | 3.8 | 3.17 |
| Real earnings | 2.3 | −1.0 | 2.1 | 1.36 |
This experience suggests two potentially interesting cases, that is where wages and GDP grow at similar rates as in the first subperiod, and where wage growth is about half that of GDP as in the third column of the table.[26] We assume that labour force growth is 1.25 per cent per annum which is near its current average.[27] This is probably an optimistic assumption as the participation rate could well rise with falling unemployment and rising wages. Initial values for the variables in the short-run adjustment equation are taken at their 1997:Q4 levels, including an unemployment rate of 8.4 per cent.[28] The short-run scenario results are sensitive to the initial values as they involve levels variables.
The following scenarios are, of course, meant only to be indicative of possible results and are in no way predictions. After reviewing them we shall look at ways in which changes in our assumptions might affect their outcomes.
In scenario 1 shown in Figure 10, we assume that output growth is raised immediately to the SIRG and held there. In the case in which wage growth is half output growth, by March 2000 unemployment would be down to 7.4 per cent and by December 2002 to 4.9 per cent. Inflation would fall to, and stay around, 1 per cent per annum. By comparison, if output growth is initially raised to 5.5 per cent, but then brought back to 5 per cent after one year and to the SIRG after two years, inflation will rise, but remain in the 2–3 per cent band (Figure 11). Under the optimistic scenario (real wages grow at half the rate of output), the unemployment rate falls to 7.2 per cent after two years and 4.5 per cent after four. Note that the labour force and employment grow at rates that are approximately constant, and that the shape of the curve in these scenarios is driven by the rise in E/L, where the change in the unemployment rate, δu, is given by 100*{E/L}(Δl−Δe) and Δl is growth in the labour force, L.
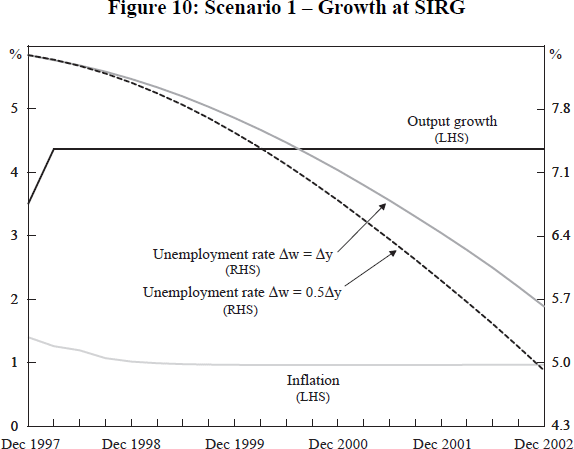
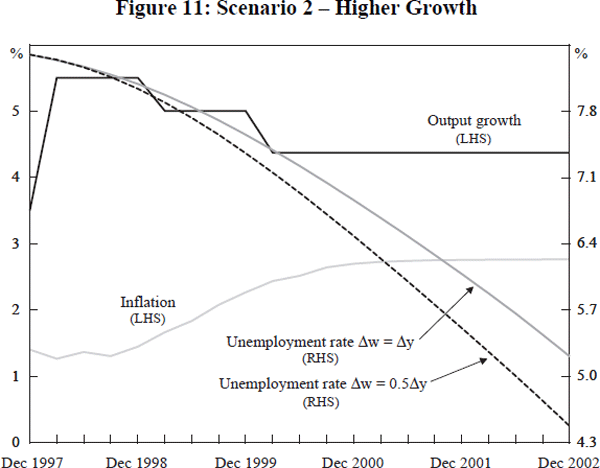
The final figure (12) compares unemployment paths using the optimistic wage assumption cases of scenarios 1 and 2, with the outcome arising from the 1998–99 Budget growth assumption. We suppose this implies that growth is 3.5 per cent for the first quarter of 1998 and then 3 per cent until the end of 1999, thereafter reverting to the SIRG. The results are not particularly different in the first year, but leave the economy with half a percentage point more of unemployment, when compared with the high growth case, by the year 2000. A qualification to these outcomes is that the Asian currency crisis has led to a depreciation of the $A which will ensure that the overall inflation rate will be higher than we have calculated, given our neutral assumption about import prices.
One approach to this type of scenario is to construct them using long-run wage and output elasticities. This can give very different results. Figure 12 includes a case in which the scenario of growth at the SIRG is constructed from only long-run elasticities, rather than the complete adjustment process of Equation (23). It can be seen that this gives a much lower reduction in unemployment. The reason is that the long-run elasticities are very long run, applying to an equilibrium in the distant future where growth of output and wages have ceased. Putting this another way, the long-run elasticities relate to levels of output, whereas the adjustment process in the estimated equation deals with growth. The difference between the results in the two cases comes from the ‘short run’ elasticity that relates the growth in output (Δy) to the change in employment (Δe). The consequence is that the long-run elasticity procedure suggests smaller falls in unemployment than the case which allows for short-run adjustments.
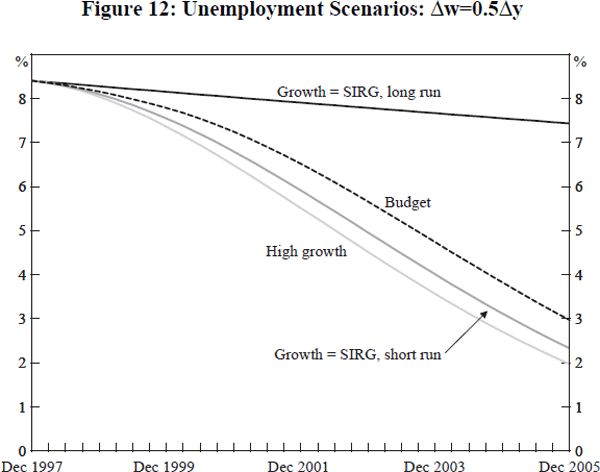
Unemployment falls with growth and declines significantly more rapidly in the optimistic wage scenario. In scenario 2, after four years, unemployment is back near the rate before the 1982–83 recession. It is doubtful that anything like this will be achieved, given the recent slowdown in some of our Asian trading partners. However, even the low growth case, where the Budget estimates assume lower growth because of the Asian situation, still shows worthwhile reductions in unemployment. Our calculations suggest that it would take nine years from the end of the 1990–92 recession to reach 1989 unemployment rates. Perhaps one of the main lessons is to illustrate how drastically recessions affect unemployment, given that it takes so long to reverse their impact on unemployment.
As we have noted, rises in participation could reduce the fall in unemployment. Another offset could come from the additional rises in wages which a period of prolonged growth could produce. Further, rising real wages may have a greater negative impact on growth than we have allowed for via the ‘scale effect’ when the economy is on the supply curve.[29] Our assumptions about the relationship between output and wage growth become less likely to hold, the further the system moves from the base date. Nevertheless, our results raise the possibility that higher growth could contribute significantly to reducing unemployment.
Other scenarios which make alternative assumptions about the behaviour of the workforce could well show smaller reductions in unemployment, as it is likely that the participation rate would rise considerably during a long period of growth of output, wages and employment. These responses are one of the least understood facets of the labour market.
6. Concluding Remarks
Low unemployment was the norm for Australia during the thirty years following World War 2. This is too long a period for ‘full employment’ to be dismissed as a transient or rare event, so it must remain a challenge for economists to find how to recover it. At the macroeconomic level, faster economic growth and less drastic recessions are the main ways of reducing unemployment. This is not a panacea, because higher growth will bring the potential for rising inflation. Our object has been to investigate the concept of a GDP growth rate compatible with steady inflation, and we find an association between growth and domestically generated inflation that is at least as robust empirically as many alternative approaches. This is also supported by approaching the relationship indirectly through a version of the output gap concept and relating growth to the gap. Our figure for the steady inflation rate of growth (SIRG) for the post-float period is 4.37 per cent per annum.
Inflation also arises from fluctuations in import prices and this, as often as not, takes the form of a negative impact. We argue that inflationary pressures from this source should be absorbed by allowing the overall inflation rate to move up or down, rather than by reducing growth below the SIRG. Some of Australia's most severe inflationary episodes, such as the Korean wool-price boom and the oil price shocks, have come from such external sources. The pegged exchange rate system of those times was not well suited to absorbing such shocks, but a floating rate system at least allows an independent monetary policy.
If import price inflation is falling, there will be some scope for growth above the SIRG to help achieve falling unemployment without rising inflation. Further, if as seems very likely, the economy continues to produce growth cycles there will be scope for higher growth than the SIRG in the upswing. If this is not the case, there will be a tendency for the average inflation rate to lie under the target band and even to fall so low that there is difficulty in conducting effective monetary policy in times of recession.
Given the poor state of knowledge about the elasticities of demand for, and particularly supply of, labour, there must be doubt as to the extent to which growth can contribute to reducing unemployment. However, our scenarios suggest that it might be possible to bring unemployment down to the vicinity of 1989 pre-recession rates over the next four to five years if actual outcomes for growth and wages approximate those of our optimistic assumptions, or even those of some of our less optimistic cases. Historically, periods of high activity and growth such as in World War 2 and during 1945–75 were accompanied by low unemployment. It would be surprising if growth were not the cause of such favourable employment experience.
Macroeconomic measures to promote growth without rising inflation would no doubt have greater effect in more flexible labour markets. Nevertheless, it should not be forgotten that rigidity in labour markets characterised postwar Australia much more than at present. Given that most microeconomic measures to reduce unemployment aim to create structural change, it is likely that they too would work better in an environment of high growth.
Appendix A: Data Definitions
E: Quarterly total non-farm employment taken from the NIF database on DX [VNEQ.AN_NNE].
HR: Quarterly total average weekly hours (seasonally adjusted) from the NIF database on DX [VNEQ.AN_NHT].
M: Quarterly implicit price deflator for imports from the TSS database on DX [NPDQ.AD90IMP#].
p: Quarterly Treasury underlying Consumer Price Inflation rate taken from the TSS database on DX [RSR.U190C9211001].
W: Quarterly real earnings index (seasonally adjusted) taken from the RBA database on DX [GLCREISA]. This series is constructed by the RBA taking total earnings from the national accounts to create a weekly earnings figure and then deflating by the relevant consumption index (see the ‘Notes to Tables’ to Table G.5 in the Reserve Bank Bulletin).
X: The exchange rate – defined as the inverse of the trade-weighted index from the RBA database on DX [FXRTWI]. Quarterly data derived as the average of the end-month figures.
Y: Quarterly Australian real GDP(A) (seasonally adjusted) taken from the ABS TSS database on DX [NPDQ.AK90GDP#A].
Capital letters denote data in levels and lower case denotes logged series.
Appendix B: Estimation Results
B.1 Inflation
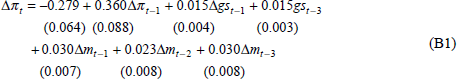
LM test for serial correlation 0.968 RESET test 0.766
Normality (Jarque-Bera) 1.424 Heteroskedasticity 0.343
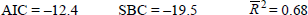
Estimation period: 1983:Q4 – 1997:Q4
B.2 Employment
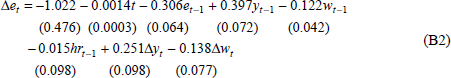
LM test for serial correlation 3.938 RESET test 1.830
Normality (Jarque-Bera) 0.465 Heteroskedasticity 0.035
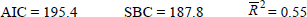
Estimation period: 1984:Q4 – 1997:Q1
The series were all found to be I(1) using the standard ADF tests. Details are available from the authors.
Appendix C: Results with Alternative Data
C.1 Output gap and growth
The output gap series is measured as the difference between real output at any given time, and a twelve-period moving average of real output adjusted so that the June 1990 observation is the same as actual GDP. Real output in June 1990 was chosen as a period of potential output, as it was a time intermediate between boom and recession. The correlation coefficient between the two series over the period 1983:Q4 to 1997:Q4 is 85 per cent. More details on the use of the output gap as an alternative to growth in estimating Equation (10) are available in Pitchford and Dungey (1998).
C.2 Import price inflation and the exchange rate
If the changes in the inflation rate of the TWI, denoted Δh, are substituted for the import price component, re-estimating Equation (24) yields:
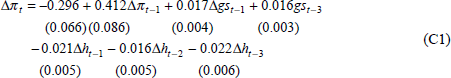
LM test for serial correlation 2.435 RESET test 0.582
Normality (Jarque-Bera) 1.324 Heteroskedasticity 0.023
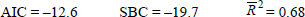
Estimation period: 1983:Q4 – 1997:Q4
The negative signs on the changes in exchange rate inflation come from the definition of the TWI as an index of the prices of foreign currencies (see Equation (14)). Hence, an early indication of the import price component's effect on inflation can be had from movements in Δh.
Footnotes
We would like to thank Jeff Borland, Guy Debelle, Bruce Chapman and Lou Will for helpful discussions and comments on the paper. [*]
We were tempted to use the term NAIRG, but chose not to perpetuate an improper use of the concept of acceleration. [1]
Even in the US there are doubts about the stability and value of the NAIRU concept (Symposium on the natural rate of unemployment in the Journal of Economic Perspectives, Winter, 1997). [2]
Other reasons include wage-fixing systems that have little or no relation to market forces, poverty traps and other institutional factors affecting the reservation wage of the unemployed. [3]
This curve would have horizontal sections where there are minimum wages, which would show up both at low wage levels and higher levels if market forces are prevented from affecting real wages. To the extent that they apply to subsectors of the workforce, they would appear as a lower slope of LE. [4]
In principle, prices of exports should enter these equations. However, for Australia, the proportion of exports that directly enter the price index is small. Also, empirical results do not justify their inclusion. [5]
There is no survey information available for Australia on the expectations of those who set prices. [6]
Strictly, the m in Equations (1) and (3) are different variables, the first being the import component of the CPI (for which there is no adequate data) and the second, the import price deflator from the National Accounts. [7]
It is, of course, not possible to insulate against relative price movements of goods whose prices are determined on world markets. See Pitchford (1993) and the references therein. [8]
An alternative would be to incorporate into the equation(s) those variables, such as the behaviour of reserves, which distinguish a pegged from a floating system. [9]
Snooks (1998) and in earlier works argues that inflation is a necessary concomitant of growth. He investigates this in a very long-run historical context and with recent data for various OECD countries. Apart from the generation of inflation by growth, our approach differs from his in that we also allow for the effect of prices of imports and for expectational effects that feed back on inflation. [10]
From this account of potential output, it could vary over the cycle. However, our procedures estimate an average and we do not attempt to measure its cyclical movement. [11]
If potential output were defined as µ(g) they would differ only by the initial value of x and
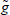 .
[12]
.
[12]
There is no evidence of a moving average in the errors induced by the use of quarterly differences of the annual inflation rate. [13]
The restriction that the coefficients on Δgst-1 and gst-3 were equal could not be rejected. This was tested in the original equation with the equivalent test that the coefficients βi in Equation (9) were equal, thus preserving correct size in the test. [14]
It is sometimes claimed that expectational effects are asymmetrical in that, for instance, reducing inflation requires more foregone growth than the extra growth required to raise inflation. Hence we looked for asymmetrical responses of inflation by including the signs of independent variables in the regressions, but the results were insignificant. Another matter examined was whether the stage of the cycle (e.g. time since the trough) might affect the degree of responsiveness to the growth rate, but the results did not support this either. [15]
For the pre-float period (1972–83), the correlation coefficient for the regression of m on h is 16 per cent. [16]
An exception could be if there was asymmetry in the response of expected inflation between rises and falls in the expected rate. We did not detect such an effect. [17]
Those definitions which use some general price level in a foreign country must pick up effects from non-traded good prices and differing tastes and trade structures that would seem to have little significance for domestic import prices. [18]
See, for example, Hamermesh (1993). [19]
The economy would have operated on the labour demand curve if the period considered could be characterised as one of excess supply of labour. However, our theoretical analysis implies that this cannot be inferred without knowing the effective supply curve. [20]
Russell and Tease modify the unit labour cost series by using smoothed GDP in its construction. We can obtain similar results to theirs using the unit labour cost data. However, the data needed for a study of employment should be per head of employees, not per unit of output. [21]
A consistent real wage growth rate can be calculated more accurately, for example at 5.6 per cent for a 0.5 per cent rise in employment, but is less useful for analytical purposes. [22]
See Stolper and Samuelson (1941), Meade and Russell (1957) and Pitchford (1963) for analyses of this, the latter papers establishing that almost anything can happen. [23]
The Taylor rule involves adjustment to both output and inflation, so could be extended to a growth target. It would also need modification so that it distinguished between sources of inflation. [24]
This exercise is undertaken by Debelle and Vickery (1998). [25]
The Accord experience in the 1980s is unlikely to be repeated. [26]
Other cases are examined in Dungey and Pitchford (1998). [27]
These simulations use the employment equation in Appendix B and assume no change in average weekly hours. [28]
See Debelle and Vickery (1998) for a discussion of the scale effect. [29]
References
Barro, R. and H. Grossman (1976), Money, Employment and Inflation, Cambridge University Press, Cambridge.
Commonwealth Treasury (1996), Documentation of the Treasury Macroeconomic (TRYM) Model of the Australian Economy, CPN Printing, Canberra.
Crosby, M. and N. Olekalns (1998), ‘Inflation, Unemployment and the NAIRU in Australia’, Australian Economic Review, forthcoming.
Debelle, G. and J. Vickery (1998), ‘The Macroeconomics of Australian Unemployment’, paper presented at this conference.
Dungey, M. and J. Pitchford (1998), ‘Employment, Growth and Real Wages in Australia’, mimeo, La Trobe University.
Gregory, R. (1986), ‘Wages Policy and Unemployment in Australia’, Economica, 53(210S), pp. S53–S74.
Hamermesh, D. (1993), Labor Demand, Princeton University Press, Princeton, New Jersey.
Malinvaud, E. (1977), The Theory of Unemployment Reconsidered, Basil Blackwell, Oxford.
Meade, J. and E. Russell (1957), ‘Wage Rates, the Cost of Living and the Balance of Payments’, Economic Record, 33(64), pp. 23–28.
Muellbauer, J. and R. Portes (1978), ‘Macroeconomic Models with Quantity Rationing’, Economic Journal, 88(352), pp. 788–821.
Pitchford, J.D. (1963), ‘Real Wages, Money Wages and the Terms of Trade’, Economic Record, 39(87), pp. 282–291.
Pitchford, J.D. (1993), ‘The Exchange Rate and Macroeconomic Policy in Australia’, in A. Blundell-Wignall (ed.), The Exchange Rate, International Trade and the Balance of Payments, Reserve Bank of Australia, Sydney, pp. 147–201.
Pitchford, J.D. and M. Dungey (1998), ‘An Analysis of Inflation and Growth in Australia’, mimeo, Australian National University.
Russell, W. and W. Tease (1991), ‘Employment, Output and Real Wages’, Economic Record, 67(196), pp. 34–45.
Snooks, G.D. (1998), Long Run Dynamics, Macmillan/St Martins Press, London and New York.
Stevens, G. (1992), ‘Inflation and Disinflation in Australia: 1950–91’, in A. Blundell-Wignall (ed.), Inflation, Disinflation and Monetary Policy, Reserve Bank of Australia, Sydney, pp. 182–244.
Stolper, S.F., and P.A. Samuelson (1941), ‘Protection and Real Wages’, Review of Economic Studies, 9, pp. 58–73.