RBA Annual Conference – 1993 Major Influences on the Australian Dollar Exchange Rate Adrian Blundell-Wignall, Jerome Fahrer and Alexandra Heath
1. Introduction
In December 1983, Australia abandoned its management of the exchange rate, ushering in a period of floating rates which has continued until the present. This decision to float the Australian dollar ($A) lagged behind that of the major countries, which ceased their commitment to fixed parities in March 1973. Over the course of the decade to the end of 1983, Australia moved through several transitional exchange rate regimes, each more flexible than its predecessor. However, none proved satisfactory from the perspective of conducting monetary policy in a world environment characterised by the increasing globalisation of financial markets and major swings in both inflation and economic activity. Speculative capital flows periodically undermined attempts to reconcile objectives for the exchange rate and macroeconomic stability. The decision to float was taken with monetary policy considerations in mind, but against the background of more general moves to deregulate the financial system.
Since then there has been considerable debate in Australia about the causes of swings in the $A, particularly during 1985 and 1986. Strongly held views about the role of speculators, the influence of Australia's cumulating current account deficits, sharp swings in Australia's terms of trade and the impact of monetary policy have been central to the debate. In the mid-1980s, the exchange rate depreciated as the terms of trade declined and the current account deficit rose. Some argued, however, that the exchange rate went further than could be justified by ‘fundamentals’, adding a fillip to inflation. During the 1990s, the exchange rate has again declined as interest rates have been steadily reduced and the terms of trade have fallen. The subject of whether the causes of this depreciation are nominal (with adverse consequences for inflation) or real (contributing to external adjustment), is again creating dilemmas for policy makers. To assess such issues requires some knowledge of the relative importance of the various influences on the $A exchange rate.
This paper reviews Australia's experience with managed exchange rates during the 1970s and early 1980s and with floating exchange rates in the past 10 years. It examines the broad characteristics of fluctuations in the $A, often comparing these with the behaviour of exchange rates in other countries. In this process, various hypotheses about factors that influence the $A are examined and tested with quantitative techniques. Section 2 reviews the historical experience since the early 1970s. Section 3 sets out some of the major elements of exchange rate economics and comments both on international empirical evidence and the extent to which it is relevant to the $A. Empirical estimates of a long-run equilibrium model for the real $A exchange rate are discussed in Section 4 and some attempt is made to relate these to earlier findings about the broad behavioural characteristics of the $A. Some concluding remarks are offered in Section 5.
2. The Historical Background
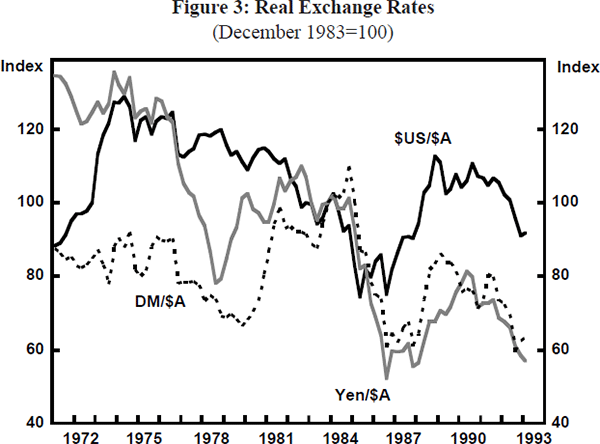
From the early 1970s until the late 1980s Australia's inflation rate was higher than that of most other OECD countries. This is shown in the steadily rising relative price line for Australia versus a weighted average of other countries in Figure 1 and for Australia versus the United States in Figure 2. This inflation differential was associated with long-run nominal exchange rate depreciation – both against the trade-weighted basket of currencies (Figure 1) and the US dollar ($US) (Figure 2). Over the longer run, there has also been some depreciation of the real exchange rates (nominal rates deflated by relative prices) shown in both figures. Thus, not all of the nominal depreciation which has occurred in the past two decades has been eroded through higher inflation. Similar trends are also broadly confirmed for the real bilateral rates against the yen and the deutschemark (DM) shown in Figure 3.
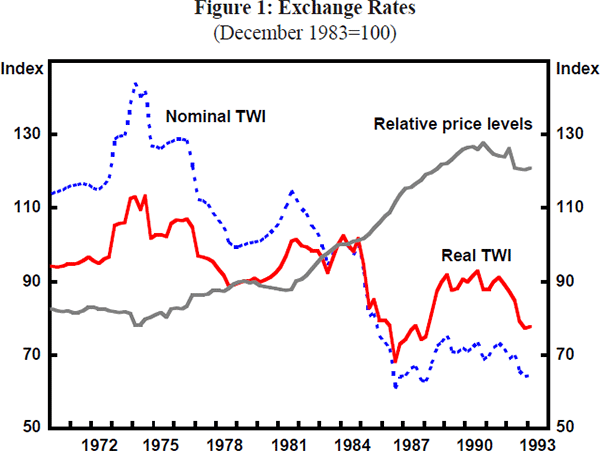
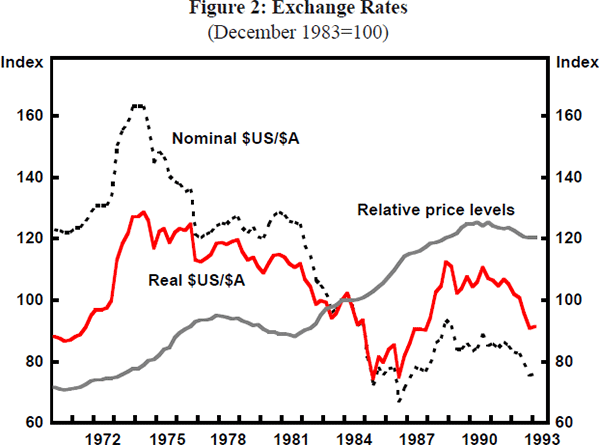
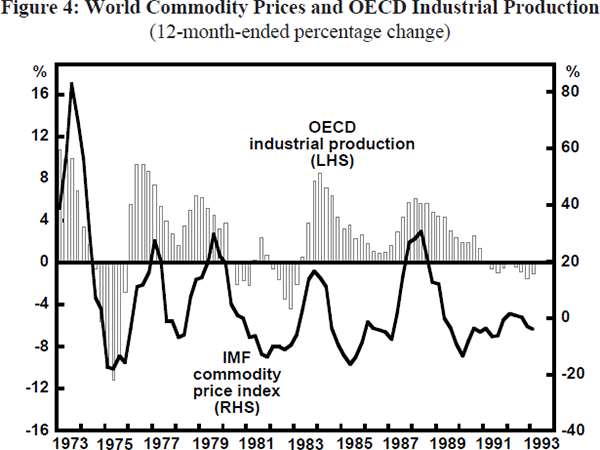
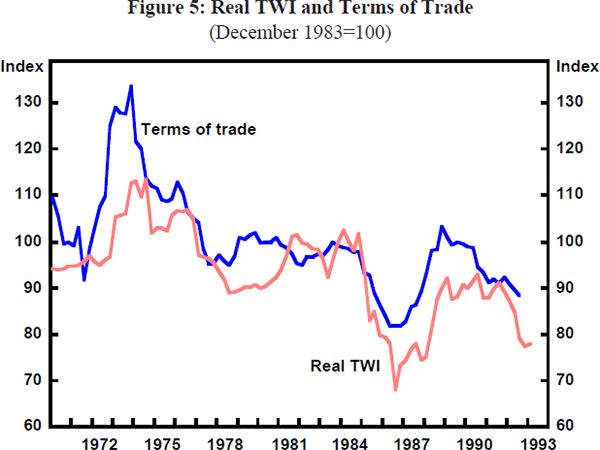
Around these longer-run trends both nominal and real exchange rates have been subject to quite major fluctuations. These fluctuations reflect a number of factors, including major swings in the terms of trade. While its exports have become more diversified recently, Australia is still predominantly a commodity exporting country. Commodity prices are highly volatile, and are driven primarily by the strength or weakness of the world economy, represented by OECD industrial production (Figure 4). Peaks and troughs of the world commodity price cycle shown in Figure 4 are highly correlated with Australia's terms of trade, shown in Figure 5. Since the early 1970s, movements in the terms of trade as large as 45 per cent have occurred in the space of a couple of years, although movements of 10 to 25 per cent have been more common since the early 1980s. The apparent impact of these large real external shocks on the real exchange rate is clear from Figure 5. Other factors, however, must be important as well, since there are often short-to-medium run divergences in the movements of the real exchange rate from those in the terms of trade. Moreover, since the mid-1980s, there appears to have been a sustained downward movement in the real trade-weighted index (TWI) relative to the terms of trade. Subsequent discussion helps to draw out what some of these additional factors appear to have been during particular episodes.
Since 1970 there have been six broad phases in the behaviour of the nominal and real exchange rates that deserve special consideration:
- 1970–1973, when the $A appreciated in nominal and real terms in the face of a rising terms of trade;
- 1974–1976, when the $A depreciated as the terms of trade declined;
- 1980–1983, when the nominal and real TWI appreciated with no apparent upward movement in the terms of trade;
- 1985–1986, when depreciation crises under floating rates appeared excessive in relation to the terms of trade decline at the time;
- 1987–1989, when the $A appreciated as the terms of trade rose; and
- 1990–1993, when $A depreciation in the face of a declining terms of trade appeared to be somewhat delayed and relatively orderly.
Each of these periods is discussed in turn.
2.1 Managed Exchange Rates
The various managed exchange rate regimes prior to December 1983 were accompanied by capital controls and widespread regulations in the domestic financial system.
2.1.1 The world commodity price boom of the early 1970s
Under the system of fixed exchange rates established at the Bretton Woods Conference in 1944, the $A was pegged to the pound sterling. This system came under extreme pressure during the early 1970s, when current account imbalances suggested fundamental disequilibria among major OECD countries. This led to substantial changes to international monetary arrangements during the course of 1971 and, towards the end of the year, the $A was revalued and pegged to the $US instead of the pound. However, attempts to bolster the Bretton Woods system quickly proved to be inadequate. The $US was devalued in December 1971 and February 1973, with the decision by major countries to float finally being made in March 1973.
Australia did not follow suit and at first tried to maintain its peg to the $US. However, as Australia's terms of trade rose sharply with the world commodity price boom of the early 1970s, a number of changes in the parity between the $A and the $US occurred. The sharp rise in the terms of trade led to a positive real income transfer equivalent to between 4 and 5 per cent of gross domestic product (GDP) between 1972 and 1974, exacerbating inflationary pressures which, with fixed exchange rates and increasing international reserves, were imported from abroad. The $A was revalued three times, though not sufficiently to avoid a marked acceleration of inflation.
2.1.2 Terms of trade weakness and depreciation 1974–1978
Dissatisfaction with the $US as an anchor currency during the early 1970s began to arise largely because it was being subjected to continuous downward pressure. In 1973, the $A depreciated in real terms against the yen and the deutschemark (Figure 3), in spite of the underlying strength of the economy. Economic circumstances changed in 1974 when the terms of trade began to decline, falling by about 24 per cent between early 1974 and the middle of 1975, and the $A was devalued 12 per cent against gold and the $US in September 1974. At the same time it was decided to unhitch the currency from the fortunes of the $US in favour of fixing the exchange rate against a basket of currencies. Under this arrangement, the external value of the $A was varied to offset movements of other currencies against the $US.
This regime, too, proved unsatisfactory when the terms of trade were subject to renewed downward pressure from 1976. The fixed nominal exchange rate and relatively high domestic inflation soon led to the perception that the $A had become overvalued. This, in turn, caused a marked fall-off in private capital inflow to finance the current account. Speculation about devaluation caused investors to delay bringing funds to Australia, anticipating that assets would soon be cheaper. Foreign exchange reserves began to fall precipitously and the Government devalued the $A by 17.5 per cent in November 1976. At the same time, the perception of the need for greater flexibility in exchange rate management led to the abandonment of the system of fixing against a basket of currencies in favour of a crawling peg against the $US. Under this new regime a small group of officials (the so-called ‘troika’) kept movements of the TWI under review, adjusting it via the daily peg against the $US.
2.1.3 The crawling peg and effective appreciation in the early 1980s
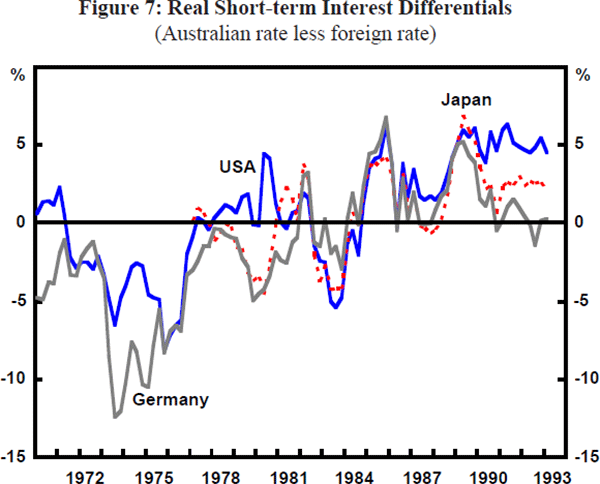
Tight monetary policy in some OECD countries, notably the United States and Germany, and rising world energy prices led to a marked weakening of OECD economic activity during the early 1980s (Figure 4). However, Australia is relatively rich in energy resources and through this period the terms of trade held up comparatively well. Indeed, there was a sense of euphoria about prospects for the energy and minerals sectors following the second major OPEC oil price rise, which led to an investment boom in 1981. This boom saw the current account deficit widen to nearly 6 per cent of GDP (Figure 6). Inflation was already high at around 10 per cent and demand pressures threatened to drive it further out of line with developments in other countries. Monetary policy was tightened in 1981 and 1982, and real interest differentials at the short and long end moved in Australia's favour, particularly against countries other than the United States (Figures 7 and 8). This combination of circumstances saw the $A more or less hold ground against the soaring $US and appreciate sharply against the yen and the deutschemark. As a result, the TWI rose in early 1981 and, given Australia's relatively high inflation rate, this appreciation was sustained in real terms, even in the face of some subsequent nominal depreciations, until the middle of the 1980s.
The euphoria surrounding the minerals boom proved to be misplaced. On the one hand, the OECD area entered a major recession in the early 1980s, so there was not a lot of demand for Australia's minerals and energy. On the other hand, the large wage claims that had been agreed to in anticipation of major increases in production proved to be excessive and generated inflationary pressures. These circumstances led to a perception that the exchange rate had become overvalued in early 1983. This, together with great uncertainty about the future policies of the incoming Government, led to intense speculation and heavy capital outflow, in spite of the presence of exchange controls designed specifically to inhibit such linkages.[1] Eventually, the exchange rate was devalued by 10 per cent in the first half of the year. This was followed by heavy capital inflow in the second half of 1983, apparently in anticipation of an appreciation of the crawling peg, as confidence in the policies of the new Government began to grow. Effective monetary policy required these inflows to be offset. While the authorities could have tried to deal with such flows through direct controls, these were seen as being out of keeping with the desire to reduce distortions in financial markets. Another option was to float the dollar. When the $A was floated on 12 December, foreign exchange controls were dismantled virtually overnight.
2.2 Floating Exchange Rates
The move to a floating rate regime was expected to improve the efficiency of the financial system, consistent with broader financial deregulation at the time, while giving the authorities greater control over domestic monetary policy. This was expected to be associated with a rise in the volatility of exchange rates, compared with the various pegs and crawling pegs which preceded it. Before discussing the depreciation crises of the mid-1980s which did see volatility rise to an historically high level, it is worth placing this issue in perspective. To this end, Figures 9, 10 and 11 show measures of the moving average of monthly volatility measures for a number of bilateral and trade-weighted exchange rates.[2] Prior to the float, the volatility of the $US/$A exchange rate and the TWI were broadly similar to those of some other major exchange rates, while $A volatility against non-US currencies was always relatively high. This picture was little changed during the first year of the float.
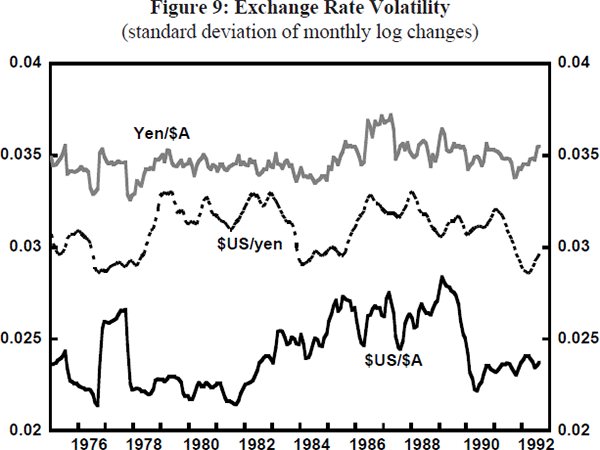
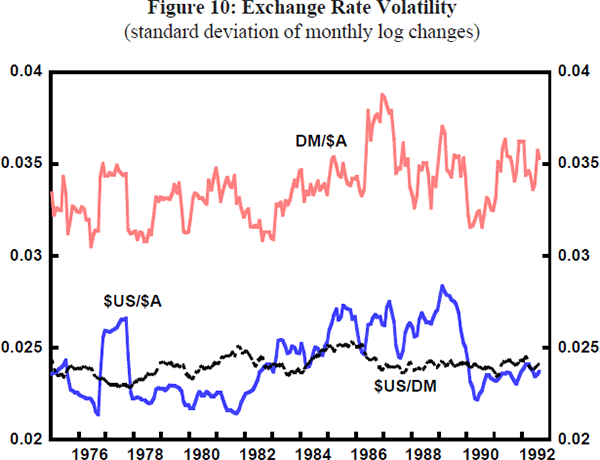
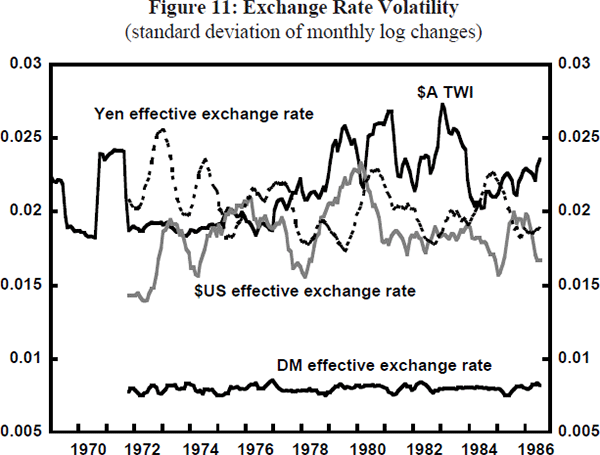
During the mid-1980s, however, there were some changes to these volatility patterns:
- $US/$A volatility rose;
- $A volatility against third currencies rose to even higher levels; and
- the volatility of the TWI rose from being similar to that of most other major currencies to being above them.
Subsequently, in the late 1980s and the early 1990s, $A volatility declined across-the-board. In this latter period it is fair to say that the $A has been no more volatile than any of the major currencies. Nor is it much more volatile, on average, than it was during the period of managed exchange rates. The relatively high level of volatility in the mid-1980s appears more related to events specific to that period, than to the advent of floating exchange rates as such.
2.2.1 Floating rate crises in 1985 and 1986
The sharp rise in $A volatility in the mid-1980s was associated with major sustained changes in the exchange rate level. From January to the end of April 1985 the $A depreciated by over 20 per cent against both the $US and the TWI. While relative stability in these exchange rates was regained for a time and the $A actually appreciated until July, this was followed by further depreciation which gathered pace in the middle of 1986. The $A fell 17 per cent from May to the end of August 1986. Overall, the TWI depreciated by more than one-third from its level at the end of 1984, to its lowest point at the end of July 1986. The causes of these large downward adjustments appear to have involved both nominal (monetary) and real factors, as well as significant changes in market psychology.
There were four potentially important and interrelated factors that appear to have influenced exchange rate developments from the beginning of 1985. The first was that the exchange rate had become overvalued in the early 1980s, and this had not been corrected by early 1985. Moreover, at that time, commodity prices began to weaken, leading to a 13 per cent decline in the terms of trade in 1985 and 1986. This caused an increase in the current account deficit. These circumstances required real exchange rate depreciation in an underlying equilibrium sense. Correction to overvaluation in circumstances where the equilibrium rate itself is declining was bound to require large nominal and real depreciation. However, judging by the abnormal level of exchange rate volatility in these years and the extent to which domestic inflation rose subsequently, there are grounds to believe that other factors also drove the exchange rate lower.
The second factor concerns the outlook for inflation, which may have been particularly important in the timing of the February 1985 phase of the depreciation. In late January 1985, the authorities ceased the practice of announcing projections for the M3 monetary aggregate. In one sense this decision was understandable, since financial deregulation under way at the time rendered the traditional monetary aggregates increasingly difficult to interpret. The M3 target, however, was not replaced by any clear alternative focus for inflation expectations. Moreover, cash rates fell at first as the Reserve Bank had difficulty in mopping up the excess cash in the system caused by a public sector strike, which affected the processing of tax payments. The unofficial ‘cash rate’ fell to a low of 5.5 per cent on 6 February, rising to a peak of 13.25 per cent on 13 February. In an environment where some Federal ministers were calling for a continued commitment to full wage indexation, these developments contributed to the feeling of increased uncertainty about the future path of inflation.
Against this background, the Reserve Bank began to tighten monetary policy. By March 1985, unofficial cash rates had been pushed up to around 15 per cent, some two percentage points higher than their late January level. While the exchange rate had stabilised at its lower level for a time, it fell again in November, possibly triggered by further adverse balance of payments news and higher-than-expected money supply growth. The Bank became a strong buyer of Australian dollars at this time, and cash rates were raised sharply again. These actions served to reverse most of the November depreciation, eventually permitting some easing of cash rates. Relative to other countries, however, overall monetary policy was significantly tightened throughout 1985. Three-month real interest rate differentials favouring the $A rose to between 4 and 7 percentage points against other major countries by late 1985 (Figure 7).
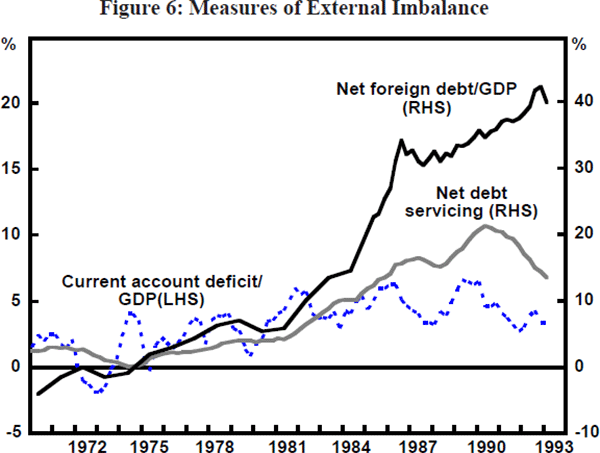
The third factor influencing exchange rate movements in the mid-1980s was a marked increase in the perceived riskiness of investing in Australia as a consequence of the sharp rise in external debt. This was particularly important in the second major bout of depreciation in 1986. While Australia had experienced terms of trade and balance of payments fluctuations before, the sustained and rapid rise in foreign debt was a new and troubling phenomenon. Net debt as a share of GDP had risen from around 5 per cent of GDP at the beginning of the 1980s to about 14 per cent in 1984, as the current account imbalances of the early 1980s began to cumulate.[3] Partly driven by exchange rate valuation effects, this leaped to around 25 per cent by the end of 1985 and to over 34 per cent in 1986.[4] On 14 May 1986, the Treasurer made his often-quoted ‘banana republic’ remarks, and the problem of external debt and its links with underlying structural imbalances in the economy was emphasised much more in policy discussions. The spectre was raised of Australia not being able to grow quickly enough to meet its net foreign interest payments without pushing the level of debt even higher as a share of GDP. The credit worthiness of Australian debt was downgraded by ratings agencies and the $A slid from around 72 US cents in mid-May to about 60 US cents by the end of July. Negative sentiment and exchange rates around these low levels persisted throughout most of August.
The fourth factor affecting the exchange rate during the mid-1980s was the presence of destabilising speculative cycles, evidence for which is reported in the empirical results below. In the absence of a firm anchor for monetary policy, and given concerns about the terms of trade, the balance of payments and external indebtedness, the market appeared to lack a clear idea of how far the exchange rate had to fall. In this environment, rumours triggered disproportionate movements in the $A. In 1985, the MX missile crisis helped to trigger the early depreciation of the $A. In the lead-up to July 1986 (which saw the low point for the $A) several factors appeared to contribute to further falls in the currency driven by speculative runs. These included the announcement (subsequently withdrawn) that exemptions to withholding tax were to be abolished, rumours that the Treasurer had resigned and talk of Japanese sales of Australian bonds. Ex ante pressures over very short horizons were enormous by any standards. Exchange rate movements of 2 to 3 per cent during the course of a single day occurred on several occasions during the mid-1980s.
During the 1986 episode, the Reserve Bank increasingly used the twin tools of buying Australian dollars and tightening monetary policy. Cash rates were pushed up sharply from the 9 per cent to the 13 per cent range in the first half of May, to around 15 per cent towards the end of the month. Rates were then allowed to drift down for a time, before being pushed up to around 17 per cent by the end of August. To a very large extent these activist policies reflected the view that while fundamentals required downward adjustment of the $A, adverse market psychology risked pushing it too far, with potentially adverse consequences for price and wage inflation.[5]
2.2.2 Terms of trade and exchange rate strength 1987–1989
The driving force influencing the currency in 1987 and 1988 was the strength of world demand, which pushed commodity prices up by around 49 per cent from July 1986 to their peak in January 1989. Between late 1986 and the first quarter of 1989 Australia's terms of trade rose by over 26 per cent, exerting substantial upward pressure on the nominal and real exchange rates.[6]
The almost continuous rise of the $A in 1987 and 1988 occurred in spite of considerable changes in the overall stance of monetary policy. Policy was at first eased through 1987, with cash rates falling substantially.[7] Falling interest rates and the rising terms of trade stimulated economic activity, particularly in the second half of the year. By 1988 the economy was booming. Business confidence and investment were strong, and the current account actually improved in 1987 and the first half of 1988, as national saving rose through the highly successful efforts of the public sector to curb its borrowing. However, policy makers became concerned about the sustainability of the boom, particularly in light of rapid asset price inflation. By April 1988, monetary policy began to tighten.
Similar concerns about the strength of demand in the US economy also saw interest rates being ‘snugged’ upwards. However, the stronger tightening in Australia saw short-term interest differentials move sharply in favour of the $A (Figure 7). This reinforced the favourable impact of the terms of trade on the currency during most of 1988. From its low point of around 60 US cents in mid-1986, the $A rose by some 49 per cent to around 89 US cents in January 1989. Over this same period, the TWI rose by 35 per cent and for most of this period the Reserve Bank was a net purchaser of foreign exchange.
Tight monetary policy persisted through 1989. However, the final surge of investment through the course of the year, much of it speculative, could not be financed from national saving. While the public sector accounts remained in sound shape, corporate borrowing continued to be associated with further declines in private sector saving. The current account had begun to deteriorate again in late 1988 and this gathered momentum through 1989. In response to these developments and aggressive sales of Australian dollars by the Bank, there was a downward adjustment in the exchange rate in February, in spite of favourable interest rate differentials and the strong terms of trade.
2.2.3 Declining terms of trade and firm monetary policy in the 1990s
By the beginning of the 1990s monetary policy was also tight in most other countries that had experienced asset price inflation in the late 1980s (the Anglo-Saxon countries, Japan and a number of Scandinavian countries). For quite different reasons interest rates were also rising in Europe. German unification required a major transfer of resources within Europe to finance investment in and income support transfers to the East. At the same time, with nominal exchange rates constrained by the European Monetary System (EMS), high German interest rates were imposed on other European countries. If nominal exchange rates could not adjust, the required adjustment in real exchange rates had to be generated by even faster deflation of Germany's main trading partners. This configuration of developments in the world economy was strongly biased towards deflation and OECD industrial production slowed. Commodity prices fell from early 1990, exerting strong downward pressure on the terms of trade – circumstances which have persisted more or less until the present.
These external circumstances are similar to those of the mid-1980s, yet exchange rate outcomes during the 1990s bear little resemblance to the chaotic episodes of that period:
- after declining somewhat in early 1990, the currency strengthened later in the year, when Gulf War factors were influencing world exchange markets, peaking in September at around 83 US cents with a TWI of 62;
- the $A then depreciated about 5 to 6 per cent over the following half year before strengthening again to 80 US cents with a TWI of 61 in September 1991; and
- from September 1991 to May 1993 the $A depreciated by about 15 per cent against the $US and 18 per cent against the trade-weighted basket. In this period intervention was aimed at preventing excessively rapid declines and, at times, there were short periods of upward pressure on the exchange rate.
Compared with other periods of terms of trade decline, the exchange rate depreciation was noticeably delayed. When the depreciation did come, it was much more orderly than in the mid-1980s.
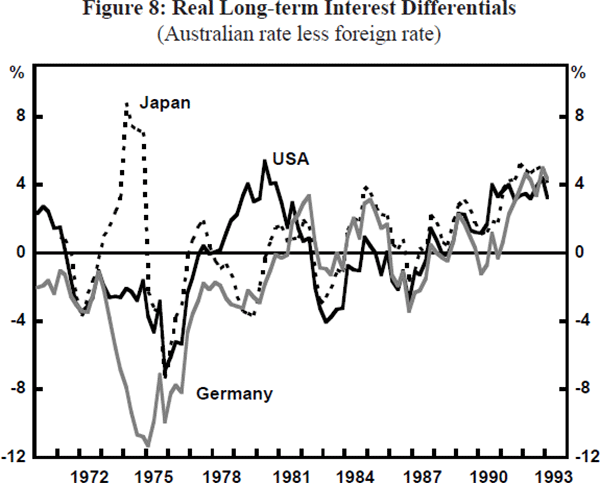
The main reason for this seems to be the relative absence of the three factors other than the terms of trade that played such important roles during the mid-1980s, i.e. concerns about inflation and monetary policy, the perceived unsustainability of the leap in foreign debt, and bandwagon speculative cycles. With regard to the first of these, it is clear that the inflation concerns of the mid-1980s have been greatly reduced. While cash rates have been steadily lowered from the high levels necessary to puncture the asset price boom and related spending of the late 1980s, most easings have been broadly conditional on declining inflationary expectations. Real interest rates have remained significantly positive. Short-term real interest differentials have remained high vis-à-vis the United States, positive against Japan and negative only in relation to Germany, where monetary policy has been very tight. Long-term real interest differentials have continued to rise in favour of the $A vis-à-vis all major currencies for much of the early 1990s.
The fact that Australian long-term bonds rates have appeared high in relation to inflation has caused domestic and foreign buyers to purchase them in anticipation of capital gains. This has provided considerable support for the currency. Bond yields have in fact fallen from around 13.5 per cent in 1990 to 7.5 per cent in 1993.
The second favourable contrast with the mid-1980s is that the 1990s have been much less associated with concerns about unsustainable growth in foreign debt. Indeed, through a remarkable growth in exports, the goods and services balance has been in surplus for a good part of the 1990s and the current account deficit has mostly been less than 4 per cent of GDP. Furthermore, the net servicing cost of the foreign debt as a percentage of exports of goods and services has been falling during the 1990s, mainly because of lower interest rates. While foreign debt has continued to grow as a share of GDP, there have been no major leaps in indebtedness comparable with that in the mid-1980s.
The third contrast with the mid-1980s is that the depreciation has been relatively orderly and destabilising speculative cycles have not dominated exchange rate outcomes. There are a number of reasons for this. Firstly, such cycles are not independent of the broader environment in which they occur. In this respect, low inflation and the very clear direction of monetary policy have been particularly helpful. Secondly, the increased depth and maturity of the foreign exchange market may be a factor. Finally, foreign exchange market intervention may have had some success in promoting orderly market conditions.
3. Stylised Facts About Exchange Rates and the Long-Run Equilibrium
The above discussion has sought to place major movements in the $A exchange rate in their historical perspective. In so doing, it has focused on factors thought to be important in influencing the currency in each particular episode. Amongst the many influences discussed, five seemed to be of particular importance:
- Australia's terms of trade;
- net foreign indebtedness;
- domestic investment booms that could not be financed adequately out of domestic saving;
- real interest differentials; and
- speculative factors not based on any ‘fundamentals’.
But how do these factors fit in with the economics of exchange rates? Do they lend themselves to a more formal modelling of the $A? In this respect, it is worth stating from the outset that attempts to model month-to-month, or quarter-to-quarter, changes in exchange rates have failed quite badly. The out-of-sample forecasting performance of structural exchange rate models has typically been inferior to the predictions of a simple random walk model.[8] One reason often cited for this is that these models are typically based on the assumption of market efficiency, which may not apply. Indeed, international research has repeatedly questioned whether foreign exchange markets fit into the efficient markets paradigm. Since this issue is so important in forming an overall strategy on how empirical statements about exchange rates might be made, it is worth mentioning it from the outset.
3.1 Exchange Market Efficiency
The concept of ‘efficiency’, as it applies to financial markets, has a narrow and precise interpretation: that market participants should not be able to derive excess returns by systematically exploiting available information. Arbitrage eliminates such opportunities, so that all of the information available at any point in time is reflected in the price of the asset in question.
3.1.1 Uncovered interest parity: inefficiency and risk premia
Provided ‘political’ risk arising from regulations etc. does not exist so that covered interest parity (CIP) holds, and provided participants in the foreign exchange market are neutral with respect to other country-specific risks, then efficiency in the sense described above implies that expected returns on comparable assets should be equalised. If this were not the case, expected excess returns would be available. Thus, if the interest rate in country A exceeds that in B, this must be matched by an exactly offsetting expected depreciation of currency A against currency B, and uncovered interest parity (UIP) is said to hold:

The first part of this expression is CIP in which the interest differential 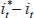 equals the forward
premium fpt. This should equal the expected appreciation
of the nominal exchange rate
equals the forward
premium fpt. This should equal the expected appreciation
of the nominal exchange rate 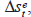 where st
is the logarithm of the nominal exchange rate (foreign currency per unit of
domestic currency) and e
denotes expectations. Therefore, UIP also implies that the forward price of foreign
exchange should equal the expected future spot
price.[9]
where st
is the logarithm of the nominal exchange rate (foreign currency per unit of
domestic currency) and e
denotes expectations. Therefore, UIP also implies that the forward price of foreign
exchange should equal the expected future spot
price.[9]
Intuitively, the reason for this should be quite clear. A deviation of the forward rate from the expected future spot rate should be eliminated by market participants seeking profits. If the $US/$A forward rate for payment one period ahead is higher than participants think the $US/$A spot rate will be, then opportunities exist to profit by selling the $A forward and buying $A back on the spot market in one period's time, when the forward contract expires. This process will drive the forward rate down towards equality with the expected future spot rate. If efficiency and risk neutrality prevail, then the forward market for foreign exchange should provide all of the information on expected future spot rates. In econometric terms, the forward rate should be an unbiased predictor of the future spot rate, i.e. there should be no systematic errors in market participants forecasts of the future spot rate.
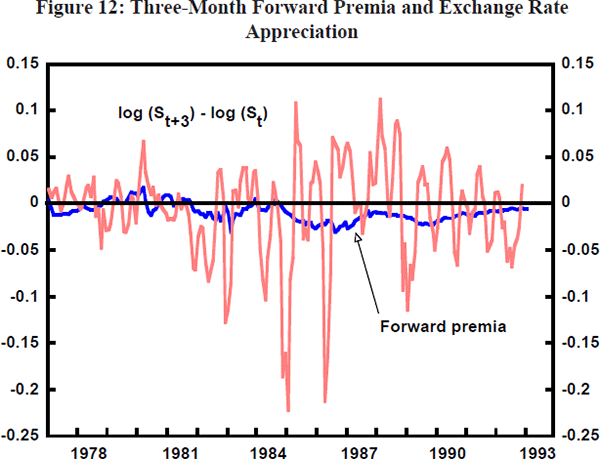
Tests of efficiency and risk neutrality, however, have been generally rejected in the literature: the forward rate is a biased predictor of the future spot rate.[10] Figure 12 shows the three-month forward premium between the $A and the $US, as well as the difference between the logarithms of the current and three-month ahead spot rates. It is clear from the figure that forward rates have not proved to be efficient predictors of future spot rates in the foreign exchange market. The $A has continually stood at a discount to the $US since 1985. During this period there have been episodes of persistent appreciations, for example, in 1986/87 and 1987/88. There have also been episodes of persistent depreciations well in excess of the forward discount, for example, in 1985 and 1988/89. Formal tests of UIP set out in Appendix B confirm its rejection on Australian post-float data. The forward rate is a biased predictor of the future spot rate.
3.1.2 ‘Political’ and country-specific risk
The assumption of risk neutrality is essential if the forward price of foreign exchange is to equal the expected future spot rate. If this assumption is violated, the forward price reflects not only the expected future spot rate, but will also include premia for risk involved in currency speculation. These premia drive a wedge between the expected future spot rate and the forward rate:

where prpt is a ‘political’ risk premium deriving
from regulations and rpt
is a risk premium on foreign-currency-denominated assets. Expected appreciation is
equal to the forward premium less the (time-varying) risk premia on foreign
currency assets. Equivalently, the logarithm of the forward price of foreign
exchange ft,t+1, contracted in period t
for delivery in one period's time, exceeds the logarithm of the expected
future spot rate 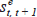 by the sum of ‘political’
and country risk premia. This has led some to speculate that UIP may fail,
not because of any market inefficiency, but because of the presence of these
time-varying risk premia.
by the sum of ‘political’
and country risk premia. This has led some to speculate that UIP may fail,
not because of any market inefficiency, but because of the presence of these
time-varying risk premia.
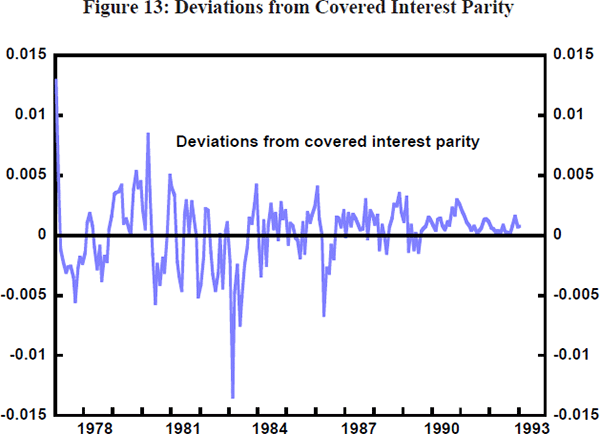
The first condition to check when interpreting UIP is whether or not the foreign exchange market is free of regulations and controls that distort prices, regardless of how market participants behave. A straightforward test for the absence of ‘political’ risk premia in exchange rates is a test for CIP. Except for minor transactions costs, the hedged yield on comparable domestic and foreign assets should be equal. That is, the difference between the spot and forward exchange rates between two currencies should equal the interest differential between the two relevant countries. Figure 13 shows deviations from covered interest parity from 1980 to the present for the $US/$A rate. Prior to 1984, such differentials were often large. Subsequently, they have declined to small values which arise from transactions costs and measurement error (except for the 1986 withholding tax episode). Formal tests set out in Appendix B confirm that since 1984, CIP holds for the Australian dollar.[11]
Since ‘political’ risk is excluded, the next thing to check is whether
a time-varying country risk can explain the bias in the forward rate as a predictor
of the future spot rate. This is more difficult, because the bias may be due
either to systematic expectational errors or to a time-varying risk premium,
and neither is directly observable. Froot and Frankel (1989) attempt to disentangle
this ambiguity by making use of a variety of sources of survey data on exchange
rate expectations. Given fpt and survey-based measures of 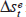 in equation (2), the
risk premium is directly (though imperfectly) measurable. This enables the
authors to decompose the bias in the forward rate as a predictor of the future
spot rate into that due to the presence of the risk premium and that due to
systematic prediction errors. They find that the ‘lion's share’
of the bias is explained by expectational errors.
in equation (2), the
risk premium is directly (though imperfectly) measurable. This enables the
authors to decompose the bias in the forward rate as a predictor of the future
spot rate into that due to the presence of the risk premium and that due to
systematic prediction errors. They find that the ‘lion's share’
of the bias is explained by expectational errors.
Survey data for Australia are collected by the firm MMS International. Formal tests in Appendix B confirm that the MMS-measured risk premium is responsible for essentially none of the $A forward rate bias. These measures are, however, only as good as the expectations survey. In particular, it is difficult to believe that responses to the MMS survey questions about expected future spot rates are (or indeed can be) independent of the forward rate. No systematic risk appears to have emerged in the 1980s according to the MMS measure, which fluctuates around zero. Nevertheless, it is not implausible that the rapid growth in net foreign liabilities as a share of GDP during the 1980s has led to world investors demanding a higher expected return on $A assets than on foreign assets.
In summary, it does seem reasonable to take very seriously the proposition that failures of UIP may be the result of divergences from market efficiency and that systematic forecast errors imply the presence of information which, if systematically exploited, would enable abnormal returns to be made.
3.1.3 Inefficiencies and the role of feedback traders
One of the most plausible explanations for inefficiencies offered in recent years is that ‘noise’ and ‘feedback’ traders play an important role in foreign exchange markets – traders whose demand for assets is based on the history of past returns, rather than expectations about fundamentals. This idea has been offered to explain the empirical regularities that exchange rates are positively autocorrelated over short horizons (recent past increases will be correlated with current increases) and negatively autocorrelated over longer horizons (the cumulation of rises over a long enough period will predict falls in the exchange rate).[12] Cutler, Poterba and Summers (1990a) found these patterns in the excess returns for such a wide range of asset markets and countries that they concluded they are an inherent feature of the speculative process, rather than the result of risk premia associated with specific country and asset market features. They offer a model to explain these phenomena with different groups of speculators: those which are fundamentals-based and efficient; those which base their demands on fundamentals observed with a lag; and feedback traders.[13] Because ‘news’ about fundamentals is incorporated into prices with a lag, speculators following feedback rules make profits while increasing the variability of the asset prices, even though fundamentals eventually assert themselves. Autocorrelation patterns of excess returns for the $US/$A exchange rate set out in Appendix B are consistent with the findings of Cutler, Poterba and Summers (1990a).
3.2 Empirical Modelling Based on Longer-Run Tendencies
As mentioned earlier, structural time series models, to date, have failed to explain short-run movements in exchange rates adequately. This is likely to be explained, at least in part, by the inherent difficulty of incorporating inefficient speculation mechanisms into these models. An alternative strategy is to be relatively less ambitious and focus on what can be said about longer-run or equilibrium tendencies of the real exchange rate resulting from the behaviour of economic fundamentals. The actual real exchange rate may deviate from the equilibrium level for a variety of reasons. Monetary policy influences the nominal exchange rate in the short run and, since goods prices at home and abroad adjust only slowly, the real exchange may be influenced temporarily. Similarly, feedback traders may drive exchange rates away from fundamentals over short horizons. In all of these cases, however, fundamentals should assert themselves in the longer run. Provided the theory of real exchange rate behaviour in equilibrium can be specified, empirical techniques (cointegration and error-correction methodology) enable such relationships to be identified from time series data. Shorter-run exchange rate behaviour that is not explained by fundamentals can then be examined separately – for example, to see whether the exchange rate displays evidence of the presence of feedback traders, or of the effects of short-run monetary policy changes that lead to the Dornbusch (1976) form of overshooting, and so forth.
With regard to empirical modelling, this strategy requires that the long-run equilibrium determinants of the $A be specified. From the historical discussion in Section 2, the apparent importance of the terms of trade, external indebtedness and ex ante savings-investment imbalances in explaining broad real exchange rate trends, suggests a clear role for balance of payments theories about the equilibrium value of the currency. The following section attempts to sketch out a broad and greatly simplified outline of this approach to real exchange rate determination, in an attempt to motivate the subsequent empirical approach.
3.2.1 The balance of payments and the equilibrium real exchange rate
The long-run equilibrium real exchange rate at any point in time should be that which is consistent with a country maintaining a sustainable current account balance.[14] A reasonably precise statement of the balance of payments identity of one country against another, or one country against the rest of the world, is:

where a is net foreign assets as a share of wealth, b is the trade surplus as a share of wealth, and ρ is the average interest rate on net foreign assets minus the growth rate of wealth, that is assumed to be constant. The trade balance (as a share of wealth), following Frenkel and Mussa (1985), is assumed to be given by:

where q = s + p − p* is the logarithm of the real exchange rate, p is the logarithm of the domestic price level and p* the logarithm of the foreign price level. The variable z summarises exogenous real factors that affect domestic and foreign excess demand for domestic goods.
The current account surplus defined by equations (3) and (4) must be willingly held in portfolios. The desired rate of accumulation of net foreign assets by domestic residents adjusts the stock of net foreign assets to the desired stock, which is in turn adjusted for the risk premium on foreign currency assets:

where ad is a variable reflecting the desired stock of net foreign assets in the absence of any risk premium, r is the real interest rate with a maturity equal to the observation interval, and Δqe is the expected change in the real exchange rate over that interval. The coefficient β reflects the responsiveness of desired net foreign assets to variations in risk premia. This relationship implies the uncovered interest parity condition in real terms, with a risk premium equal to (1/β)(a − ad).
This simple framework provides the basis for analysing the equilibrium level of the
real exchange rate. In the long run, equilibrium net foreign assets should
be stabilised as a share of wealth (Δa = 0), and the real exchange rate is expected
to be constant
(Δqe = 0). Letting a bar denote
the currently expected equilibrium level of a variable, this implies that the
equilibrium trade surplus 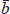 equals ρ
multiplied by the equilibrium level of net foreign liabilities
equals ρ
multiplied by the equilibrium level of net foreign liabilities 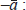

It also implies that:

Equilibrium net foreign assets differ from their desired level in the absence of risk by the risk premium multiplied by a coefficient related to risk aversion.
Combining these last two expressions yields an equilibrium relationship between the real exchange rate, factors influencing domestic and foreign excess demand for domestic goods, and the level of net foreign assets:

In Frenkel and Mussa (1985), 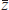 and
and 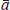 at any point in time
will come to depend on the expected future paths of z and a.
If they evolve as random walks, however, the theoretical model is greatly simplified.
The best forecasts of future values of z and a are their
current levels. That is, the equilibrium value of the real exchange rate comes
to depend on the current levels of the variables in z, and the current
level of a. Two further points are worth noting. Firstly, if the explanatory
variables are not stationary in their levels, then neither is the equilibrium
value of the real exchange rate unless the z's form a cointegrating
relationship. Secondly, in this case, the model would meet the requirements
for using cointegration and error-correction methods in its empirical application.
at any point in time
will come to depend on the expected future paths of z and a.
If they evolve as random walks, however, the theoretical model is greatly simplified.
The best forecasts of future values of z and a are their
current levels. That is, the equilibrium value of the real exchange rate comes
to depend on the current levels of the variables in z, and the current
level of a. Two further points are worth noting. Firstly, if the explanatory
variables are not stationary in their levels, then neither is the equilibrium
value of the real exchange rate unless the z's form a cointegrating
relationship. Secondly, in this case, the model would meet the requirements
for using cointegration and error-correction methods in its empirical application.
3.2.2 Terms of trade and investment shocks
The intuition behind the z variables in equation (8) is relatively straightforward. Factors that create current and expected future excess demand for domestic goods require exchange rate adjustment to ensure equilibrium. If, for example, these factors led to decreased demand for domestic goods by foreigners, the trade balance would deteriorate. Given the level of net foreign assets (or liabilities) and net interest flows, this would be inconsistent with balance of payments equilibrium without exchange rate depreciation to raise foreign demand. Following the ‘dependent economy’ traded and non-traded goods framework, domestic excess demand for traded goods in Australia would, for the balance of payments equilibrium to be maintained, require exchange rate depreciation. Domestic excess demand for non-traded goods, on the other hand, would require the exchange rate to appreciate to switch demand towards traded goods.
For a commodity-exporting country like Australia, the terms of trade are particularly important in influencing current domestic and foreign excess demand for domestic goods. A rise in the terms of trade reflects strong demand for Australian commodities by the rest of the world. Such a relative price shift, if it is perceived to be permanent, implies a permanent real income transfer to Australia from the rest of the world. This increases domestic demand for both traded and non-traded goods, and at a time when foreign demand is already strong. In the absence of a rise in the exchange rate, the relative price shift also causes domestic producers to switch towards exporting commodities. The exchange rate rises to offset these tendencies, switching demand towards imports of foreign goods. These mechanisms are set out more formally in Blundell-Wignall and Gregory (1990).
Figure 14 shows a scatter plot of Australia's terms of trade and the real TWI, in order to give a visual impression of longer-run tendencies in the data. Even though other possible influences on the real exchange rate are not held constant, the relationship is quite striking: there is a clear positive relationship between the terms of trade and the real exchange rate, as predicted by the equilibrium balance of payments theory.
The other important factor related to excess demand referred to in Section 2 was the apparent importance of ex ante investment demand shocks. Such a shock was prominent in 1981, when euphoria over prospects for the minerals and energy sectors drove up investment demand, longer-term real interest rates compared with the rest of the world and the real exchange rate.[15] Similar pressures emerged during the investment boom of the late 1980s. How does this fit in with long-run exchange rate determination from a theoretical perspective?
An ex ante permanent rise in investment demand is an important component
of 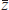 , since it reflects
not current, but expected future excess demand for domestic products from home
and abroad. The marginal productivity of capital rises, but actual capital
accumulation must be financed out of saving. The additional saving can be generated
by reduced domestic consumption, or by attracting incremental saving from the
rest of the world. Shifting saving from the rest of the world requires a deterioration
in the balance of trade in the current period, in order to generate an even
better trade performance later on. This intertemporal aspect of the relationship
between ex ante
investment demand and expected future excess demand (from home and abroad) for domestic
products is a potentially important aspect of real exchange rate and long-term
real interest rate
dynamics.[16]
, since it reflects
not current, but expected future excess demand for domestic products from home
and abroad. The marginal productivity of capital rises, but actual capital
accumulation must be financed out of saving. The additional saving can be generated
by reduced domestic consumption, or by attracting incremental saving from the
rest of the world. Shifting saving from the rest of the world requires a deterioration
in the balance of trade in the current period, in order to generate an even
better trade performance later on. This intertemporal aspect of the relationship
between ex ante
investment demand and expected future excess demand (from home and abroad) for domestic
products is a potentially important aspect of real exchange rate and long-term
real interest rate
dynamics.[16]
In theory, an ex ante rise in investment demand in the presence of perfectly integrated and flexible goods markets would lead to only ex ante pressure on the real interest rate. The real exchange rate would appreciate, and foreign saving would be diverted immediately, through trade flows, to ensure ex post real interest rates were equalised between countries. However, while it is reasonable to suppose that financial markets are fully integrated, in the sense that CIP holds, goods markets are not so well integrated. Trade flows adjust only sluggishly in response to relative price signals to reallocate world savings in a manner that equalises the marginal productivity of capital between countries. This process can take many years or, in the case of developing or transforming economies, possibly decades. This is consistent with the common empirical finding that there is no long-run tendency towards real interest rate parity.[17]
In the presence of sluggish trade flows, all of the incremental saving needed to finance the ex ante rise in investment cannot be obtained immediately from abroad: the domestic ex ante investment shock becomes ‘bottled up’. The domestic real interest rate, therefore, rises relative to the foreign rate and persists at this higher level to:
- help crowd out domestic consumption by encouraging greater saving;
- crowd out some of the ex ante investment; and
- appreciate the real exchange rate to generate the required trade deficit.
The extent and persistence of these changes in relative prices depends on the length of time required for the trade balance to adjust to the new desired domestic saving versus investment imbalance.
It may be helpful to think of the recent topical example of this problem in the world economy – the need for massive ‘catch-up’ investment in eastern Germany. Informed estimates suggest this ‘catch-up’ will take 10 to 15 years. German real interest rates and the real exchange rate for the deutschemark need to be higher to ensure real resources are diverted within Germany, and between Germany and the rest of the world, to meet this investment demand. The euphoria over the minerals sector in Australia in the early 1980s has already been mentioned as an example of this same sort of mechanism. Similarly, the Australian investment boom in the second half of the 1980s, at least partly in response to perceptions of improved opportunities for trade with the rest of the world in general, and Asia in particular, contributed to higher long-term real interest rates and the strength of the $A over this period. Australia had to attract saving from the rest of the world to finance the investment at the time, in anticipation of being able to repay this borrowing through greater productive potential and exports in the future.
Figure 15 shows a scatter plot of the long-term real interest differential favouring Australia and the real exchange rate. The overall relationship is not as strong as is the case for the terms of trade. One reason why the relationship is somewhat looser may be due to the distortions to real interest rates during the high-inflation period of the 1970s, when financial markets were slow to adapt because of regulations or inertia. Another, and possibly more important reason, is that capital controls may have partly broken the nexus between real interest differentials and the real exchange rate. If these distortions are excluded, so that only the post-1984 data are shown (the triangles in the figure), a clearer positive relationship emerges.
3.2.3 Net foreign assets
The intuition behind the net foreign assets term in equation (8), assuming the world interest rate exceeds the growth rate of wealth (ρ is positive), is as follows. From an initial position of equilibrium, a higher level of net foreign assets, given world interest rates, implies higher net interest income from the rest of the world. For a given trade balance this violates the requirement that net foreign assets stabilise as a share of wealth: the real exchange rate would need to appreciate. Conversely, if the level of net foreign assets fell to the point where, for example, net foreign liabilities emerged, this would increase debt servicing costs for the domestic economy. For a given trade balance, net foreign liabilities would begin to rise indefinitely as a share of wealth. The real exchange rate would need to depreciate to restore equilibrium.
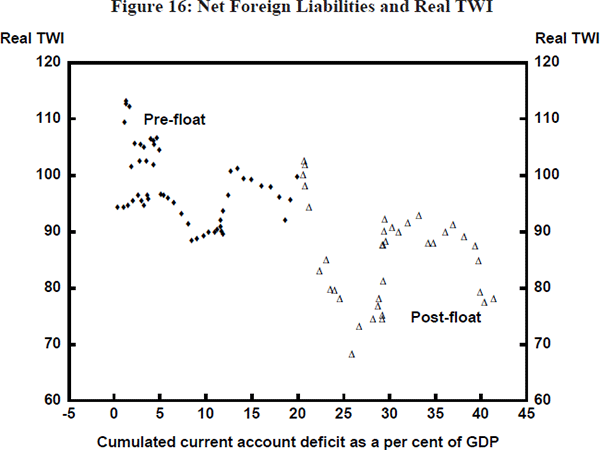
Figure 16 shows a scatter plot of the level of net foreign liabilities (measured by the cumulated current account) as a share of GDP and the real TWI. There is a clear negative relationship between the real TWI and Australia's net foreign liabilities. In terms of the way the above theoretical model is specified, there would be a positive relationship between the real TWI and Australia's negative net foreign assets.
3.2.4 The implied empirical long-run (cointegrating) relationship
The above discussion suggests that the current equilibrium level of the real exchange rate depends on the currently expected levels of the terms of trade, the long-term real interest differential and the level of net foreign assets. All of these variables are assumed to contain a unit root, i.e. they are stationary in their differences. This relationship is assumed to be of the form:
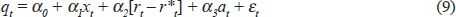
where all variables are sampled quarterly, x is the logarithm of the terms of trade, r is the long-term real interest rate, and a is the cumulated current account balance as a share of GDP. Where q refers to an effective or trade-weighted real exchange rate, r* refers to a weighted average of foreign interest rates. It is worth noting that there is a potential ambiguity with regard to the sign on a2. Whereas the exchange rate should be positively related to the real interest differential insofar as ex ante investment shocks are concerned, equation (8) suggests the exchange rate also responds positively to the long-run risk premium on foreign currency assets. If foreigners require domestic residents to hold more of their assets than domestic residents desire, then the foreign interest rate must be higher than the domestic rate in equilibrium. The higher level of net foreign assets implies more net interest income and the real exchange rate must be higher in long-run equilibrium.
4. The Empirical Findings
Each of the variables was pre-tested and found to possess a unit root (see Appendix B). The long-run coefficients in equation (8) were then estimated by the Phillips and Hansen (1990) procedure. The coefficient estimates and corrected t statistics are reported in Table 1 (see Appendix B for details). Cointegration between these variables was tested by examining the significance of the lagged residuals from the long-run equation in an error-correction model. The dependent variable is the change in the logarithm of the real exchange rate, and the regressors are the lagged residuals and current and three lagged innovations of the explanatory variables. A negative error-correction coefficient that is significantly different from zero according to a standard t test is taken as evidence that the variables are cointegrated. That is, the real exchange rate reverts to an equilibrium level depending on the terms of trade, the real interest differential and the ratio of net foreign assets to GDP.
| 1973Q2–1992Q3 | 1984Q1–1992Q3 | |
|---|---|---|
| Terms of Trade | 0.781 (4.689) |
0.885 (4.781) |
| Real Long-Term Interest Differential (vis-à-vis average world rate) |
−0.002 (−0.251) |
0.028 (2.707) |
| Net Foreign Assets (% of GDP) (cumulated current account) |
0.257 (1.716) |
0.979 (3.822) |
| Error-Correction Coefficient (unrestricted) | −0.180 (−2.042) |
−0.726 (−2.069) |
| Error-Correction Coefficient (restricted) | −0.177 (−2.400) |
−0.721 (−3.927) |
| Real ($US/$A) Exchange Rate | ||
| 1973Q2–1992Q3 | 1984Q1–1992Q3 | |
| Terms of Trade | 0.619 (2.934) |
0.800 (3.175) |
| Real Long-Term Interest Differential (vis-à-vis USA) |
0.013 (2.514) |
0.025 (2.461) |
| Net Foreign Assets (% of GDP) (less US net foreign assets as a % of GDP) |
1.181 (3.772) |
0.211 (0.364) |
| Error-Correction Coefficient (unrestricted) | −0.275 (−2.139) |
−0.989 (−1.467) |
| Error-Correction Coefficient (restricted) | −0.222 (−2.212) |
−0.360 (−1.918) |
| Note: Long-run coefficients are estimated with the Phillips and Hansen (1990) procedure. Error-correction coefficients are estimated with the log change in the real exchange rate as the dependent variable and the regressors are the lagged residuals of the Phillips-Hansen equation and the current and three lagged innovations of the explanatory variables. The t statistics are shown in parentheses. See Appendix B for more details. The restricted error-correction results exclude insignificant lagged innovation terms. | ||
Two sets of results are reported. The first is based on a long sample period, 1973Q2 to 1992Q3, which corresponds with the post-Bretton-Woods era. The second set of results is based on a shorter sample, 1984Q1 to 1992Q3, during which the $A was floating. During the latter period there were no foreign exchange and capital controls which, to the extent that they were binding previously, may have affected the links between capital flows, real interest differentials resulting from savings-investment imbalances and the degree to which net foreign liabilities were acquired. The removal of capital controls should have fewer direct implications for the terms of trade effect. The relative price and real income effects of a shift in the terms of trade work largely independently of capital controls.
4.1 Results for the TWI and $US/$A Real Exchange Rates
4.1.1 Fundamentals and the equilibrium real exchange rate
Results for the real TWI and the real bilateral $A rate against the $US are reported in Table 1. The main features of the results are as follows. Firstly, there appears to be a long-run or equilibrium relationship between the real exchange rate for the $A, the terms of trade, the long-term real interest differential and the level of net foreign liabilities as a share of GDP. Both for the real TWI and the real exchange rate against the US dollar, the error-correction coefficient is the correct sign and significantly different from zero. In the case of the long sample period, which covers both the managed and floating rate regimes, the coefficient implies that, following a random shock that drives the real TWI away from equilibrium, about two-thirds of the reversion back to equilibrium is completed in five to six quarters. Consistent with the idea that fully floating rates permit more rapid reversion to equilibrium following a shock, the error-correction coefficient for the shorter sample period is larger.
Secondly, and consistent with the earlier findings of Blundell-Wignall and Gregory (1990) and Gruen and Wilkinson (1991), the terms of trade has a powerful impact on the equilibrium level of the real exchange rate. For the TWI this coefficient is around 0.8. That is, if the terms of trade rise by 10 per cent, the equilibrium real exchange rate rises by 8 per cent. It could be argued that the causality runs from changes in the exchange rate to the terms of trade, because the pass-through of exchange rate changes is faster to the domestic price of imports than exports. To test this we estimate the model using a terms of trade variable which we know with absolute certainty to be exogenous: the ratio between the IMF commodity price index (in world prices) to a world price of manufactures. This obviously does not measure Australia's actual terms of trade as well as the ratio of the export to import price deflators. However, when used in the $US/$A regression, it leads to about the same coefficient (0.8) on the terms of trade as when the original measure is used (though it does not work as well for the TWI model).[18] This coefficient is slightly larger for the short sample period, though robust given the difference in the number of observations. The terms of trade effect on the real exchange rate does not seem to be sensitive to the presence or absence of capital controls. For the $US/$A real exchange rate, the coefficient is again of a similar order of magnitude, though slightly smaller than for the TWI results.[19]
Thirdly, the real long-term interest rate differential over the full sample period is incorrectly signed for the real TWI, but correctly signed for the real exchange rate against the $US. This possibly reflects measurement problems for the weighted-average long-term real interest rate over the managed exchange rate period, particularly with the inclusion of the Japanese rate.[20] Over the shorter post-float sample period, however, the long-term real interest differential in the TWI model has the expected sign. The impact of this variable on the real exchange rate is much stronger in the post-float period, both for the TWI and the $US/$A models. In both cases a sustained 1.0 percentage point movement of the long-term real interest differential results in about a 2.5 per cent movement in the equilibrium real exchange rate.
Finally, net foreign assets as a share of GDP appear to have a strong effect on the real exchange rate. Over the full sample period, the coefficient of 0.26 suggests that a 10 per cent rise in the share of net foreign liabilities (as opposed to assets) would result in a 2.5 per cent fall in the equilibrium level of the real TWI exchange rate. The shorter sample period results suggest an even higher elasticity for this variable.[21]
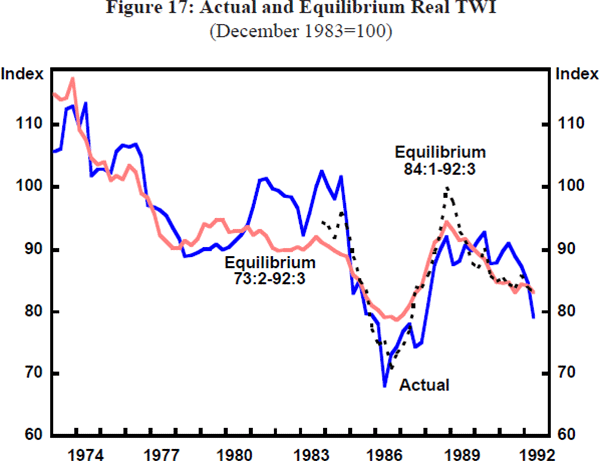
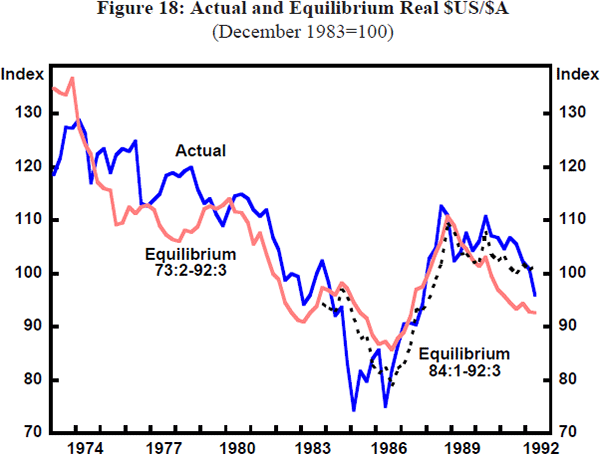
Figure 17 shows the real TWI and its calculated equilibrium values. The broken line shows the equilibrium values of the real exchange rate calculated on post-1984Q1 data. Figure 18 shows the same calculations for the $US/$A real exchange rate. The equilibrium real exchange rate tracks the broad swings in the actual real exchange rate reasonably well in both cases, though there are sustained periods of deviation from fundamentals. There are also differences in the equilibrium calculations between the post-float and long-sample models, even though the broad movements are similar. This underlines the importance of not being too precise about the ‘true’ equilibrium level of the real exchange rate. Nevertheless, the results do provide some insights into past episodes of major movements in the real exchange rate.
4.1.2 The mid-1980s episode and more recent developments
Considering first the TWI, the results suggest that the real exchange rate was substantially overvalued in the first half of the 1980s, as a consequence of the minerals boom and its aftermath. In the first half of 1985, this overvaluation was finally corrected, but at the same time fundamentals began to deteriorate. The equilibrium real exchange rate defined by the long-sample model declined steadily by about 11 per cent from March 1985 to March 1987. Between March 1985 and September 1986 the actual real exchange rate depreciated by 28 per cent, about 11 per cent more than could be justified by fundamentals. While this gap subsequently narrowed, misalignment was persistent for most of the second half of the 1980s, even when fundamentals drove the real exchange rate upwards again. If the model based on the shorter sample period is used, overshooting is reduced to about 7 per cent for the September quarter and is not sustained beyond that time. In this case, the equilibrium real exchange rate declines by about 25 per cent from March 1985 to its trough in December 1986.
There are two reasons for the larger movement of the equilibrium rate based on the post-float data. Firstly, net foreign liabilities were rising quickly at the time and this has a larger relative weight than the TWI model based on the full sample period. Secondly, fiscal tightening and deteriorating private investment expectations were associated with a sharp fall in the long-term real interest differential favouring the $A. The real interest differential has the expected sign and is relatively large over the post-float period.
There is a very similar story for the $US/$A real exchange rate results. The model based on the long-sample period attributes more of the ultimate fall in the real exchange rate to unexplained residuals than does the model based on the shorter sample period. The main explanation for this appears to be the doubling of the weight attributed to real interest differentials in influencing the equilibrium real exchange rate and a slightly higher weight on the (declining) terms of trade.
It is interesting to note that the real $US/$A exchange rate was significantly undervalued compared to its equilibrium level in 1985 and again in 1986. This finding is robust between the long-sample and short-sample results. This ‘double trough’ is absent in the case of the real TWI, which was not undervalued until 1986.
All of the models do quite well in predicting the upswing in the real exchange rate in the second half of the 1980s, as the terms of trade recovered and real interest differentials began to move in Australia's favour. The strengthening of the real $US/$A rate at this time, when the $US was weakening against most major currencies, was closely in line with the estimated rise in the equilibrium real exchange rate. However, as other major currencies, such as the yen and the DM, also strengthened against the $US, the $A does not appear to have risen sufficiently against them to keep the real TWI in line with its rising equilibrium level (see the historical experience with these cross rates in Figure 3). In principle, this should have been relatively stimulatory for economic activity.
Consistent with the historical discussion in Section 2, both measures of the real exchange rate have declined more or less in line with their equilibrium levels during the 1990s. There has been no major overshooting along the lines that occurred during the mid-1980s. Indeed, until the depreciation from the middle of 1992, the real exchange rate appears to have remained above its equilibrium level for both the TWI and $US/$A real rates.
4.2 The Unexplained Residuals
The finding of a significant long-run (error-correcting) relationship between the real exchange rate, the terms of trade, net foreign assets and the long-term real interest differential, implies that the actual real exchange rate will always revert towards its equilibrium level following a ‘disturbance’. However, the statistical properties of these long-run errors are of some interest, because they may provide some insights into the nature of exchange rate dynamics.
Figure 19 shows the estimated autocorrelation function associated with these residuals for the real TWI model estimated on the long sample period. The 95 per cent confidence interval is also shown. There is evidence of strong positive autocorrelation over short horizons. Over longer horizons, the autocorrelation function becomes negative. While the results are not shown in this paper, virtually identical autocorrelation patterns arise in the case of the real $US/$A exchange rate.
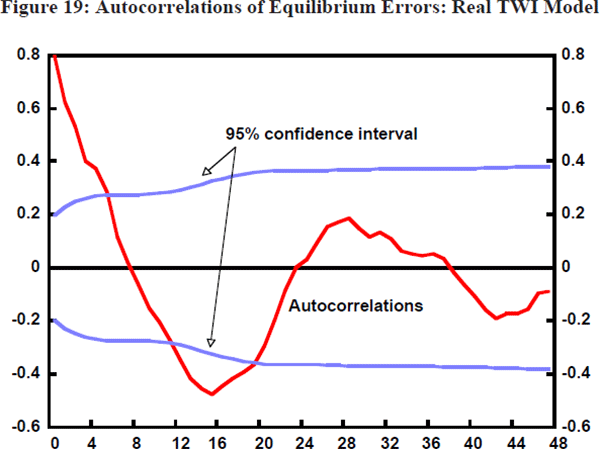
One reason why the real exchange rate might deviate from its long-run equilibrium level is the Dornbusch (1976) phenomenon of overshooting in response to monetary shocks. If monetary policy is tightened in Australia and markets are efficient in the sense set out in Section 3, the nominal exchange rate should immediately appreciate. If, however, the equilibrium level of the real exchange rate has not changed, monetary policy cannot permanently affect the level of the real exchange rate. The immediate nominal exchange rate appreciation is just sufficient to ensure that subsequent expected depreciation satisfies uncovered interest parity over the period in which goods prices are driven down relative to those abroad. The real exchange rate immediately appreciates, but subsequently depreciates as ‘sticky’ goods prices slowly adjust towards their equilibrium levels.
The reported autocorrelation results do not appear to be consistent with this form of Dornbusch overshooting, which would predict negative autocorrelation over short horizons, as monetary policy induced disturbances begin to ‘dampen’ with respect to fundamentals. The finding of positive autocorrelation over short horizons in response to any disturbance, and reversion later on, appears more consistent with the above-mentioned hypothesis that ‘feedback’ traders have extrapolative short-run expectations, reflecting the belief that new ‘trends’ persist, while basing longer-run expectations on fundamentals.
There are also a number of other possibilities. One concerns ‘noise traders’, who may irrationally perceive a random fluctuation in the exchange rate as a source of information about fundamentals on which they can profitably trade.[22] This would exacerbate the initial random movement if noise traders' beliefs were correlated, causing them to trade ‘bullishly’, while sophisticated arbitrageurs are not always present to drive them out of the market, i.e. by causing them on average to end up buying high and selling low. This market selection mechanism may be prevented from working efficiently because arbitrageurs are too risk averse to trade with a sufficiently long time horizon. Alternatively, it may take arbitrageurs time to work out that the disturbance is not based on fundamentals, i.e. they absorb information with a lag.
Another possibility is that market participants may simply not use all of the available information about fundamentals. For example, the estimation of the long-run coefficients in defining the equilibrium exchange rate allows for short-run dynamics of the explanatory variables. Consider the case of the terms of trade. There is evidence to suggest that this variable has a unit root, but it is not a random walk. In particular, only a part of any given change in the terms of trade is likely to be permanent. If market participants assume that all of the change is permanent, one would observe cumulative deviations of the actual real exchange rate from the ‘correctly-calculated’ equilibrium, followed by reversion later on.
It is of course possible that the model is not properly specified and the inclusion of other variables might eliminate the observed patterns. However, it should be recalled that more formal tests of the null hypothesis of efficiency of the foreign exchange market referred to above were rejected in the case of the $A. Moreover, positive autocorrelation over short horizons and negative autocorrelation over longer horizons was also observed for excess returns data. These combined pieces of evidence are highly suggestive of the presence of informational inefficiencies in the market for the $A.
Here it is worth noting in passing that if inefficiencies are present, then sterilised foreign exchange market intervention may have some potential to influence exchange rate dynamics.
5. Concluding Remarks
The empirical research reported in this paper is subject to the usual caveats and certainly should not be oversold. Nevertheless, a few observations are worth making.
Firstly, there is at least some evidence in the Australian data to suggest that the real value of the $A tends towards a long-run equilibrium level influenced by the terms of trade, the long-run real interest differential and net foreign liabilities. These ‘fundamental’ factors appear to explain broad trends in the real exchange rate reasonably well. There is, however, evidence of persistent deviations from fundamentals in the short run.
Secondly, the empirical evidence supports an underlying economic model that views balance of payments equilibrium as a long-run intertemporal concept. Cycles in the terms of trade have a very powerful influence on Australia's equilibrium real exchange rate. A rise in the terms of trade, for example, is immediately associated with ex ante foreign and domestic excess demand for domestic goods. This drives up the real exchange rate and helps to avoid inflation pressures that might otherwise build up. Nor does the higher real exchange rate have any serious adverse implications for net foreign assets and the balance of payments in the longer run, since the real income and substitution effects essentially offset each other.
The influences of the long-term real interest differential and net foreign liabilities on the real exchange rate, however, are somewhat more complicated. The cumulation of net foreign liabilities through time, other things being given, must reduce the equilibrium value of the real exchange rate. Put another way, the rising servicing burden associated with growing net foreign liabilities requires an improved trade balance to ensure sustainability in the longer run. If nothing else were happening, there would need to be a trend depreciation in the real exchange rate. On the other hand, an ex ante rise in investment demand which becomes ‘bottled up’ in the sense discussed above, requires the current account to deteriorate and net foreign liabilities to rise at first. The mechanism by which this occurs is a rise in the domestic long-term real interest rate and an appreciation of the real exchange rate. Provided the expected future excess demand for Australian products that stimulated the increased investment demand actually eventuates, foreign liabilities can be repaid without long-term depreciation. However, the empirical evidence reported in the paper suggests that rising net foreign liabilities have so far been associated with a trend decline in the equilibrium real exchange rate.
Nevertheless, from a policy perspective, it is worth emphasising that a rising real exchange rate and a deteriorating current account in the short run is not necessarily undesirable, provided it is associated with rising ex ante investment demand. In a low-inflation environment, sensible investment in productive capacity may well generate a high rate of return that will eventually pay for itself, regardless of past experiences.
Thirdly, formal tests of the null hypothesis of efficiency in the foreign exchange market were rejected on Australian data. Indeed, there is evidence to suggest that recent past increases in excess $A returns are positively correlated with current increases, whereas the cumulation of rises over a sufficiently long period of time eventually predicts falls in the returns. Similar patterns were observed in the persistence of deviations of the real exchange rate from its equilibrium level. Such deviations should not, in principle, display positive autocorrelation in the short run, which indicates the tendency for initial deviations to feed on each other in a cumulative manner. These patterns are more compatible with the presence of ‘feedback’ and ‘noise’ traders, possibly combined with lags and learning behaviour in absorbing information about fundamental and other factors driving exchange rates.
These informational inefficiencies create the risk of real exchange rate misalignments, with potentially damaging costs in terms of macroeconomic fluctuations and resource misallocation. Since expectations about future monetary and fiscal policies influence short-run exchange rate dynamics, well-explained policies oriented towards medium-term objectives that are understood by financial markets should help to minimise such costs.
Appendix A: Data
| Nominal Bilateral Exchange Rates | All these series were obtained from the Reserve Bank of Australia, Bulletin, Table F9. They are end-of-month exchange rates which are averaged to achieve a quarterly series. All quarterly series were converted to indexes with December 1983 as the base quarter. |
|---|---|
| Real Bilateral Exchange Rates | These were created by multiplying the quarterly nominal rates by the quarterly relative Consumer Price Index with its base in December 1983. |
| Consumer Price Indexes | All CPI series were rebased to December 1983. The Australian CPI is the Medicare and Medibank adjusted analytical series available quarterly and obtained from a Reserve Bank database. Foreign CPI measures are available monthly and were averaged to obtain a quarterly series. These rates were obtained from the OECD database on Datastream. |
| Trade-Weighted Indexes | The nominal and real Australian TWI series were obtained from a Reserve Bank database. Effective exchange rates for the USA, Japan and Germany were obtained from the IMF database on Datastream. |
| Terms of Trade | For Australia, this series was obtained from a Reserve Bank database. Foreign terms of trade were calculated from import and export price indexes which were obtained from the IMF database on Datastream. |
| Nominal Interest Rates |
All interest rates are period averages except those used in interest parity calculations and Japanese rates, which are end-of-period. Monthly observations were averaged to obtain quarterly series. The Australian rates were obtained from the Bulletin and the foreign rates were obtained from Datastream. The definitions are as follows. Short rates:
Australia (3-month Treasury Bill); Long rates:
Australia (10-year government bonds); |
| Real Interest Rates | These were calculated as: it−(CPIt/CPIt−4−1)*100, where it is the nominal interest rate. |
| Current Account Balance | All current account balances were seasonally adjusted and calculated as quarterly averages of monthly observations. The Australian balances were obtained from a Reserve Bank database; the foreign balances were obtained from Datastream. |
| GDP/GNP | Australian GDP is available quarterly and is seasonally adjusted. GNPs for the foreign economies were obtained from Datastream and are also seasonally adjusted. |
| Net Foreign Debt | This series was obtained from the Bulletin, Tables H7 and H8. It is available annually from 1976 until June 1986 and quarterly thereafter. Observations prior to 1976 were calculated by decumulating the stock of foreign debt with the flows of the current account balance. |
| Commodity Prices | This is the world commodity price index, obtained from the IMF database on Datastream. |
| OECD Industrial Production | This was obtained from the OECD database on Datastream. |
| Net Debt Servicing | This was calculated as net interest payments over total exports. |
| Expected Exchange Rates | These data were obtained from MMS International. It is the median response to the question: ‘Where do you think the $US/$A will be in four weeks' time?’ |
| Interest Parity Interest Rates | The Australian interest rate used was the weighted averages of the yields on 13-week Treasury notes at the last tender of the month (Bulletin, Table F1). The US interest rate was the end of month Treasury Bill Rate obtained from Datastream. |
| Spot and Forward Rates | These were obtained from a Reserve Bank database and were Friday 4.00 p.m. rates. |
Appendix B: Time Series Properties of the Data
B.1 Measures of Volatility
The Schwert (1989) index is used to measure the volatility of monthly nominal exchange rates. This index is calculated in three steps. Firstly, the log difference of the exchange rate in question is regressed on twelve dummy variables and twelve lagged levels of itself. Secondly, the absolute values of the residuals from this regression are regressed on twelve monthly dummies and twelve lags of this new dependent variable. The index is the predicted value of the dependent variable, scaled by a constant. The index is an estimate of the monthly standard deviation of the percentage change in the exchange rate and shows how the volatility of this variable evolves over time.
B.2 Tests of Interest Parity and Speculative Efficiency
B.2.1 Covered interest parity
If foreign exchange markets are operating efficiently, then the returns over k periods on similar domestic and foreign assets should be equalised by arbitrage i.e. covered interest parity (CIP) will hold:

where i is the interest rate on the domestic asset, i* is the interest rate on the foreign asset, St is the spot exchange rate (foreign currency per units of domestic currency, so an increase in St is an appreciation of the domestic currency) and Ft,t+k is the forward exchange rate at time t for maturity k periods ahead. Equation (B1) assumes no transactions costs and no default or political risk (e.g. the imposition of capital controls) for either asset.
A linear approximation of equation (B1) can be found by taking logs of both sides:

where ft,t+k and st are the logs of the forward rate and spot rate, respectively. Thus CIP is the condition that the forward premium, in each period is equal to the interest rate differential.
Covered interest parity is tested for by estimating the following regression equation:

where ut is an independently and identically distributed random
error. The test for CIP is that
â = 0 and 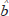 = 1. This
equation was estimated with the $US/$A exchange rate, the 13-week Treasury
note rate for Australia and the three-month US Treasury bill rate, using
monthly data over the period 1984M1 to 1993M3, with the following result:
= 1. This
equation was estimated with the $US/$A exchange rate, the 13-week Treasury
note rate for Australia and the three-month US Treasury bill rate, using
monthly data over the period 1984M1 to 1993M3, with the following result:
where method of moments standard errors are in parentheses below the estimated coefficients.
Although â is close to zero and  is close to one,
the standard errors are sufficiently small that on strict statistical grounds,
CIP is rejected by the data: the joint test that â = 0,
is close to one,
the standard errors are sufficiently small that on strict statistical grounds,
CIP is rejected by the data: the joint test that â = 0,
 = 1 is rejected
at a significance level of less than 1 per cent. This rejection possibly
reflects transactions costs or measurement error. In any case, the economic
(as distinct from statistical) departure from CIP appears to be very small.
= 1 is rejected
at a significance level of less than 1 per cent. This rejection possibly
reflects transactions costs or measurement error. In any case, the economic
(as distinct from statistical) departure from CIP appears to be very small.
B.2.2 Uncovered interest parity
Under the hypothesis of uncovered interest parity the interest differential between a foreign and domestic asset each with k periods to maturity should be equal to the expected appreciation of the domestic currency over the k periods, provided agents in the foreign exchange market are risk neutral and so do not demand a premium on the foreign asset's return, which is subject to currency risk. UIP can thus be written as:

where the right-hand side is the expectation, held at time t, of the percentage change in the exchange rate over the next k periods.
Under the assumption of rational expectations, the exchange rate expected in k periods time is equal to the exchange rate that is actually realised, plus a random error whose average value is zero:

Assuming both rational expectations and risk neutrality, the test for UIP is that
â = 0 and  = 1 in the
regression equation:
= 1 in the
regression equation:

where k=3, and which was estimated over the period 1984M1 to 1992M12 with the following results:
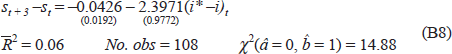
As equation (B8) shows, the hypothesis of UIP is clearly rejected. Not only is the slope coefficient significantly different from one, it is not significantly different from minus one. This result is commonplace in the literature on testing for uncovered interest parity. No economic hypothesis has been rejected more decisively, over more time periods, and for more countries, than UIP (and its near equivalent, speculative efficiency).
Since equation (B7) embodies two assumptions, rational expectations and risk neutrality, it is difficult to determine which of these maintained hypotheses is being rejected when UIP is rejected.[23] Many researchers interpret rejection of UIP as evidence of a time-varying risk premium, while still maintaining the assumption of rational expectations. However, as the risk premium is then typically defined to be the deviation from UIP, this interpretation is merely a tautology.
B.2.3 Speculative efficiency
If covered interest parity is assumed to hold, uncovered interest parity can be rewritten as:

If a=0 and b=1, the forward premium is an unbiased predictor of the expected appreciation of the exchange rate, provided, once again, that agents hold rational expectations and are risk neutral. Equation (B9) was estimated over the period 1984M1 to 1992M12 with the following results:
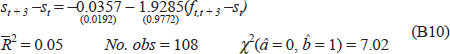
Since CIP holds, the estimated coefficients should be similar to those of the UIP regression, and this is indeed the case. The null hypothesis of speculative efficiency is rejected with significance levels of less than 3 per cent. Again, it is difficult to determine whether this rejection is due to the failure of expectations to be formed rationally, the presence of a risk premium, or both.
Froot and Frankel (1989) observe that the contribution of each of these factors to
the bias in the forward premium can be ascertained by using survey data on
expected exchange rates. They note that the regression coefficient 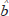 in the regression
of Δst+k on the forward premium
can be written as:
in the regression
of Δst+k on the forward premium
can be written as:

where
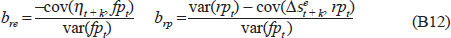
ηt+k is the expectational error based on the survey
data, fpt is the forward premium and rpt
is the risk premium, defined as the expected appreciation of the exchange
rate over k periods (also based on the survey data) minus the forward
premium. The deviation of 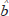 from one can therefore
be decomposed as that part due to systematic prediction errors (irrational
expectations), as given by bre and that part due to the
existence of a risk premium, as given by brp.
from one can therefore
be decomposed as that part due to systematic prediction errors (irrational
expectations), as given by bre and that part due to the
existence of a risk premium, as given by brp.
Australian survey data on exchange rate expectations are compiled by the firm MMS International, who ask a sample of between 15 and 25 foreign exchange market traders what they expect the $US/$A exchange rate to be in one month's time. The following equation using one-month changes in the exchange rate is estimated:
The estimates of bre and brp are 4.537 and −0.672, respectively. Like Froot and Frankel (1989), when one-month ahead survey data are used, all of the deviation from the null hypothesis is explained by expectational errors; indeed, risk premia do not explain a positive proportion of the bias in the forward premium.
B.2.4 Feedback trading
Table B1 below shows the average autocorrelations of the three-month excess returns from holding domestic securities (i.e. the domestic interest rate less the sum of the foreign interest rate and the appreciation of the exchange rate). It appears that the excess returns show some short-run positive autocorrelation, followed by negative autocorrelation. This evidence is consistent with the findings of Cutler, Poterba and Summers (1990a, 1990b), who find the same pattern for a variety of asset markets in the United States. They interpret this pattern as evidence for the existence of feedback traders, e.g. chartists, who impart short-run inefficiencies to the market returns. In the long run, asset prices reflect their fundamental determinants and this imparts negative autocorrelation to the excess returns.
| Months | 1–4 | 5–8 | 9–12 | 13–16 | 17–20 |
|---|---|---|---|---|---|
| Average | 0.589 | 0.199 | −0.172 | −0.424 | −0.405 |
B.2.4 Unit root tests
For each of the variables used in the structural modelling, the null hypothesis of a unit root was tested for by estimating the following regression:
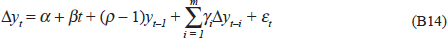
The Augmented Dickey-Fuller statistic was used to test the hypothesis that (ρ−1)=0, i.e. that there is a unit root in the data. The absence of a deterministic trend (β=0) and of drift (α=0) was also tested for as a part of this process. This equation was estimated over the period 1969Q3 to 1992Q3, or the largest subperiod for which the data are available. The data are quarterly and m is initially set to four to eliminate autocorrelation in the errors. The results are shown in Table B2 below.
| ρ − 1 | |
|---|---|
| Log (Real TWI) | 0.000 (0.443) |
| Log ($US/$A) | −0.000 (−0.288) |
| rA−r*world | −0.106 (−2.001) |
| rA−rUS | −0.096 (−1.981) |
| (CAB/GDP)A | 0.009 (2.754) |
| (CAB/GDP)A−(CAB/GNP)US | 0.004 (1.130) |
| LOG (Terms of TradeA)(a) | −0.000 (−0.204) |
| Notes: (a) 5 lags were required to eliminate autocorrelation. (b) Test statistics are in parentheses. (c) Critical values 1%: −2.60; 5%: −1.95; 10%: −1.61. (d) All α and β estimates are not significantly different from zero. |
|
The null hypothesis that ρ = 1 could not be rejected for all series except the cumulated current account series. Statistically, these series appear to have an explosive root (ρ > 1); however, in absolute terms, ρ is very close to 1 for these variables.
B.2.5 Structural models of real exchange rates
Since each of the variables used in the model contains a unit root, it is necessary to employ a modelling procedure that takes this into account and explores the possibility of cointegration between the variables in question. While the variables themselves are not stationary, a linear combination of them may be. Methods of cointegration have the advantage of modelling the equilibrium long-run relationship separately from the short-run dynamics. This allows the long-run ‘fundamentals’ to be isolated and discussed.
The Phillips and Hansen (1990) method is used to estimate the parameters of the equilibrium real exchange rate equations. This method (unlike some others) yields standard t statistics, enabling inference about whether the estimated parameters are significantly different from zero. However, this technique does not, in itself, provide a test for cointegration. To do so, the lagged errors from the long-run relationship were included in an error-correction model and tested for their significance. A significant negative coefficient on the lagged errors implies that if the real exchange rate in a certain period exceeds its long-run equilibrium value, it will tend to depreciate in the next period, although the short-run dynamics of the real exchange rate will also be influenced by other factors. However, the error-correction property ensures that the real exchange rate eventually returns to its long-run equilibrium value.
To conserve degrees of freedom, especially when the model was estimated over the short sample period 1984Q1 to 1992Q3, insignificant lags were excluded from the final specification of the error-correction model.
Footnotes
Australia was becoming more integrated with world financial markets by the beginning of the 1980s and this, together with the development of hedging facilities, served to heighten sensitivity of capital flows to developments at home and abroad. [1]
These are calculated as the Schwert (1989) index of volatility and show the standard deviation of the monthly percentage change in the exchange rate. [2]
These were caused first by the 1981 investment boom and subsequently by the marked decline in public saving. See Edey and Britten-Jones (1990) and Tease (1990). [3]
Since much of Australia's debt at the time was denominated in foreign currency, a good part of this leap was due to valuation effects of the exchange rate depreciation. In the empirical work below these effects are excluded when modelling the exchange rate, by use of the cumulated current account balance. [4]
See Macfarlane and Tease (1989). [5]
However, this was not without a final bout of nervousness in January 1987, when a realignment in the European Monetary System occurred, which was successfully countered with very strong purchases of Australian dollars and temporarily higher interest rates. [6]
Contrary to popular perception, almost all of the easing of cash rates, from 18 per cent in January to just above 10 per cent by the end of the year, occurred prior to the stock market crash in October 1987. [7]
See Meese and Rogoff (1983, 1988). These findings have been repeated frequently in the literature. [8]
Since fpt = ft,t+1−st
and 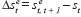 , where ft,t+1
is the forward price of foreign exchange contracted in period t
for payment in period t+1.
[9]
, where ft,t+1
is the forward price of foreign exchange contracted in period t
for payment in period t+1.
[9]
See Levich (1985), Hodrick (1987) and Froot (1990) for detailed surveys of these and other efficiency tests of the foreign exchange market. Previous Australian studies include Tease (1986) and Smith and Gruen (1989). [10]
See the OECD study by Blundell-Wignall and Browne (1991) for tests of covered interest parity for some of the major OECD countries. [11]
See Frankel and Froot (1987) and Cutler, Poterba and Summers (1990a). [12]
See Cutler, Poterba and Summers (1990b). [13]
This does not imply purchasing power parity, for reasons elaborated later. [14]
This mechanism is discussed in Gregory (1976). [15]
This relationship is often ignored in the interpetation of empirical exchange rate models, where the focus is usually on the response of the exchange rate to monetary shocks, e.g. as in the Dornbusch (1976) overshooting model. The interest rates relevant to monetary shocks are short-term rates that match the observation interval of the expected change in the exchange rate. Long-term real interest rates are not determined by monetary policy, but rather reflect the marginal productivity of capital and the marginal rate of substitution in consumption. [16]
See Cumby and Mishkin (1986) and the OECD study by Blundell-Wignall and Browne (1991). Of course, in the very long run, marginal productivities of capital will be equalised. It is assumed that this process is so long that it can be ignored for the purpose of empirical investigation. [17]
Moreover, the pass-through issue is not really relevant here because we have estimated a long-run equation, and the evidence is that the pass-through to export and import prices is complete in the long run. See Dwyer, Kent and Pease (1993). [18]
The $US results should really also include the US terms of trade. This variable was found to be insignificant for the $US/$A model. [19]
See Figure 8. The real long-term differential with Japan moves quite perversely relative to that with other countries prior to the early 1980s. Japan's relevance to Australia has probably grown significantly since the float, but was less important in the 1970s. Japanese long-term real interest rates were also more heavily influenced by administrative controls and were more prone to move inversely with inflation in earlier years. [20]
For the $US/$A model, the size of the coefficients on net foreign assets variable over the two sample periods is the reverse of the case for the TWI. The results are not strictly comparable, however, since the variable refers to net foreign assets as a share of GDP in Australia, less those in the United States. Statistical tests revealed that the cumulated current account for the United States could not be excluded from the equation. [21]
See Black (1986). [22]
Another possibility is the so-called ‘peso problem’: expectations are formed rationally ex ante, but the event that is rationally expected (the change in the exchange rate) is not observed ex post because the sample size is too small. This has the effect of making the test statistics not normally distributed, rendering invalid conventional methods of statistical inference. [23]
References
Black, F. (1986), ‘Noise’, Journal of Finance, 41(3), pp. 529–543.
Blundell-Wignall, A. and R.G. Gregory (1990), ‘Exchange Rate Policy in Advanced Commodity Exporting Countries: Australia and New Zealand’, in V. Argy and P. de Grauwe (eds), Choosing an Exchange Rate Regime: The Challenge for Smaller Industrial Countries, International Monetary Fund, Washington, D.C., pp. 224–271.
Blundell-Wignall, A. and F. Browne (1991), ‘Increasing Financial Market Integration, Real Exchange Rates and Macroeconomic Adjustment’, OECD Working Papers No. 96.
Cumby, R. and F.S. Mishkin (1986), ‘The International Linkage of Real Interest Rates: The European-U.S. Connection’, Journal of International Money and Finance, 5(1), pp. 5–23.
Cutler, D.M., J.M. Poterba and L.H. Summers (1990a), ‘Speculative Dynamics’, NBER Working Paper No. 3242.
Cutler, D.M., J.M. Poterba and L.H. Summers (1990b), ‘Speculative Dynamics and the Role of Feedback Traders’, NBER Working Paper No. 3243.
Dornbusch, R. (1976), ‘Expectations and Exchange Rate Dynamics’, Journal of Political Economy, 84(6), pp. 1161–1176.
Dwyer, J., C. Kent and A. Pease (1993), ‘Exchange Rate Pass-through: The Different Responses of Importers and Exporters’, Reserve Bank of Australia Research Discussion Paper No. 9304.
Edey, M. and M. Britten-Jones (1990), ‘Saving and Investment in the 1980s’, Reserve Bank of Australia Research Discussion Paper No. 9004.
Frankel, J.A. and K.A. Froot (1987), ‘Using Exchange Rate Data to Test Standard Propositions Regarding Exchange Rate Expectations’, American Economic Review, 77(1), pp. 133–153.
Frenkel, J.A. and M.L. Mussa (1985), ‘Asset Markets, Exchange Rates and the Balance of Payments’, in R.W. Jones and P.B. Kenen (eds), Handbook of International Economics, Vol. 2, North-Holland, Amsterdam, pp. 679–747.
Froot, K.A. (1990), ‘Short Rates and Expected Asset Returns’, NBER Working Paper No. 3247.
Froot, K.A. and J.A. Frankel (1989), ‘Forward Discount Bias: Is It an Exchange Risk Premium’, Quarterly Journal of Economics, 104(1), pp. 139–161.
Gregory, R.G. (1976), ‘Some Implications of the Growth of the Minerals Sector’, The Australian Journal of Agricultural Economics , 20(2), pp. 71–91.
Gruen, D.W.R. and J. Wilkinson (1991), ‘Australia's Real Exchange Rate – Is it Explained by the Terms of Trade or by Real Interest Differentials?’, Reserve Bank of Australia Research Discussion Paper No. 9108.
Hodrick, R.J. (1987), The Empirical Evidence on the Efficiency of Forward and Futures Foreign Exchange Markets, Harwood Academic Publishers, New York.
Levich, R.M. (1985), ‘Empirical Studies of Exchange Rates: Price Behaviour, Rate Determination, and Market Efficiency’, in R.W. Jones and P.B. Kenen (eds), Handbook of International Economics, Vol. 2, North-Holland, Amsterdam, pp. 979–1040.
Macfarlane, I.J. and W.J. Tease (1989), ‘Capital Flows and Exchange Rate Determination’, Reserve Bank of Australia Research Discussion Paper No. 8908.
Meese, R.A. and K. Rogoff (1983), ‘Empirical Exchange Rate Models of the Seventies: Do They Fit Out of Sample?’, Journal of International Economics, 14(1/2), pp. 3–24.
Meese, R.A. and K. Rogoff (1988), ‘Was it Real? The Exchange Rate-Interest Differential Relation Over the Modern Floating Rate Period’, Journal of Finance, 43(4), pp. 933–948.
Phillips, P.C.B. and B.E. Hansen (1990), ‘Statistical Inference in Instrumental Variables Regression with I(1) Processes’, Review of Economic Studies, 57(1), pp. 99–125.
Reserve Bank of Australia (1993), ‘Devaluation and Inflation’, Bulletin, May, pp. 1–3.
Schwert, G.W. (1989), ‘Why Does Stock Volatility Change Over Time?’, The Journal of Finance, 44(5), pp. 1115–1153.
Smith, J. and D.W.R. Gruen (1989), ‘A Random Walk Around the $A: Expectations, Risk, Interest Rates and Consequences for External Imbalance’, Reserve Bank of Australia Research Discussion Paper No. 8906.
Tease, W.J. (1988), ‘Speculative Efficiency and the Exchange Rate: Some Evidence Since the Float’, Economic Record, 64(189), pp. 2–13.
Tease, W.J. (1990), ‘The Balance of Payments in the 1980s’, Reserve Bank of Australia Research Discussion Paper No. 9003.