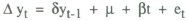RBA Annual Conference – 1989 The Relationship Between Financial Indicators and Economic Activity: Some Further Evidence Glenn Stevens and Susan Thorp[*]
Abstract
This paper supplements the earlier paper by Bullock, Morris and Stevens (BMS) in this volume, which looked at the relationship between a number of financial indicators and private final demand. The same questions are addressed in this paper, this time using more rigorous statistical techniques. Vector auto-regression (VAR) analysis is used to identify leading and lagging relationships among the data.
Results confirm that the broader money and credit aggregates generally lag activity, though there is no strong evidence, on the basis of the techniques used here, of a leading relationship from short-term interests rates (or M1) to activity. The paper suggests a complex relationship between interest rates and activity, including a policy reaction function, may exist, which cannot be satisfactorily disentangled here.
The data set of BMS is also extended in this paper to allow a preliminary examination of the tradeable goods sector. Models including the exchange rate, foreign demand and prices, as well as domestic activity and financial variables are estimated. Results from these tests suggest an effect of the exchange rate on imports and exports, which is consistent with a link between monetary policy and the tradeable goods sector.
1. Introduction
The role of money and credit in the economy, and particularly the empirical relationships between monetary and credit aggregates and measures of economic activity, have attracted much attention in the macroeconomics literature. Many prescriptions for monetary policy have arisen as a result of strongly-held beliefs about these relationships.
The aim of this paper is to explore whether a range of financial indicators – short-term interest rates, and various monetary and credit measures – have useful leading relationships with measures of economic activity.
An earlier paper by Bullock, Morris and Stevens (1989) (BMS) has already considered this issue. Its tentative conclusions were that the narrow monetary aggregate M1[1] and the level of short-term interest rates had a reasonably good relationship with private final demand, and had the added advantage of being leading indicators. Broad monetary and credit aggregates tended to be at best coincident with activity, if not lagging. The intermediate aggregates, M3 and bank lending, were useful indicators at times, principally in the early and mid-1970s, but had since been subject to considerable disturbance in their relationship with activity.
These conclusions were drawn on the basis of fairly simple methodology – graphs and correlation coefficients. The approach adopted in this paper is to take the same data set as in BMS (updated and revised for re-basing of the national accounts to 1984/85 prices) to see whether the earlier preliminary conclusions draw support from more sophisticated tests.
In recent years in particular, questions of statistical methodology have tended to dominate the empirical literature. While it is not our intention to dwell on these issues, Section 2 of the paper, which gives a brief (and far from exhaustive) review of the empirical literature, highlights some of the methodological issues. Section 3 discusses data.
New empirical work is reported in Section 4. The tests used confirm that the broader aggregates do tend to be lagging indicators of activity, but are unable to detect any systematic leading or lagging relationship between interest rates and activity. The evidence on the narrow and intermediate monetary aggregates is mixed.
Section 5 broadens the scope of the analysis by allowing for the foreign sector. In an open economy, a floating exchange rate means that changes in monetary policy can affect output of the tradeable goods sector, through the link between interest rates and the exchange rate. The data set is expanded to allow for this, and the preliminary results reported are consistent with such an effect.
2. Background
Early work for the U.S. by Friedman and Schwartz (1963) suggested that turning points in the money stock preceded turning points in nominal income. This work was extremely influential, though a similar study for the U.K. (Friedman and Schwartz (1982)) came in for trenchant criticism from Hendry and Ericsson (1983), an example of how far econometric methodology had advanced in two decades. The monetary theory of nominal income popularised by Friedman was also embodied in econometric models of the “St Louis” tradition, such as Andersen and Jordan (1968) and Andersen and Carlson (1970), where economic activity was explained (in part) by lags of a monetary aggregate.
There was also some interest in Australia in monetary aggregates and activity. Sheppard (1973), Sharpe (1975) and Davis and Lewis (1977) all found evidence for money leading real activity. Boehm (1983), in a study of the business cycle since 1948, found that M1, M3 and bank lending all led his “reference cycle”.
Some studies used simple regression analysis to test the hypothesis that money leads income, but did not actually test the alternative hypothesis, that income leads money. This approach is potentially misleading, especially when dealing with this type of macroeconomic data. Most economic time series are autocorrelated. Where there is a relationship between two variables, this means that lags of one variable will frequently be correlated with the current value of the other. Further, the order can be reversed, often with equal statistical (and theoretical) validity.
For example, suppose m is money and y income, and et and ut are uncorrelated with each other and with their own lagged values, and that
Then a regression such as
will, in all likelihood, show a significant estimate for β since β will be picking up the effect of γ and α . But to conclude from this that mt-1 causes yt or even leads it in a strict sense, is unwarranted.
Sims (1972) introduced a more general testing procedure in an attempt to distinguish more clearly between the alternative hypotheses. If mt and yt were treated as a vector, Xt = (mt yt)
then the vector autoregression
where A is a matrix of coefficients, (L) denotes the lag operator and ut is now a 2×1 vector of residuals, becomes the basic building block of the methodology. In simple language, both mt and yt are regressed on lags of themselves and lags of the other variable. Two hypotheses are tested: (i) that the coefficients on lags of m are jointly zero in the equation explaining y, and (ii) that the coefficients on lags of y are jointly zero in the equation explaining m. If (i) can be rejected, but (ii) cannot, then this is taken to be evidence of “Granger-causality” [2] from m to y.
The test for “causality” is harder to pass in this case, since lags of money have to add information for predicting current income not already present in lags of income itself in order for it to be concluded that money leads income.
Sims (1972) was able to conclude (for U.S. data) that money did indeed lead income on this basis. Sims' finding, however, has not been universal. Using similar methodology, Williams, Goodhart and Gowland (1976) found evidence of “Granger-causality” from income to money for the U.K. For Canada, Sharpe and Miller (1975) found that money led activity, but Barth and Bennett (1974) and Auerbach and Rutner (1978) found that undirectional “causation” could not be established. Sarlo (1979) found that, for Canada, the question of whether money led income depended on the exchange-rate regime: money only led for periods of floating exchange rates. Suzuki, Kuroda and Shirakawa (1988) reported that money led activity in Japan for the 1967–1987 period. For Australia, this sort of approach was used in Bullock, Stevens and Thorp (1988), where the tentative conclusion was that monetary aggregates do not, on the whole, lead measures of economic activity.
More doubt was cast over Sims' results when later studies found that the test outcomes were sensitive to model specification. Sims (1980) added interest rates to the models of money and income, and found that there was no longer strong support for money leading income. Other authors have overturned or restored the original result, with conclusions usually depending on model specification.
In many cases, these conclusions turn on how the data are detrended. Questions of econometric practice dominate this issue; these questions are taken up briefly below. The aim of present paper is to review the tentative conclusions drawn in BMS, by applying more rigorous statistical techniques to a similar dataset. A series of vector autoregressions are estimated and tests conducted to determine whether “Granger-causal” relationships exist between the variables.
3. Data
(a) Indicators of Financial Conditions and Economic Activity
The variables used in BMS were:
- the yield on 90-day bank-accepted bills;
- monetary aggregates M1, M3, and broad money;
- lending/credit aggregates; bank lending, lending by all financial intermediaries (AFI lending) and credit; and
- private final demand (PFD), both in current and constant prices.
All variables were in seasonally adjusted form, except the bill rate.
The data used in Section 4 of this paper are the same, except that:
- national accounts aggregates have been re-based to 1984/85 prices for the constant-price series;
- all series have been updated to the September quarter 1988, two quarters later than in BMS;
- GDP is used, as well as private final demand, as an indicator of activity; and
- the analysis is conducted using unadjusted (results reported in Appendix B) as well as seasonally adjusted data.
Details of data definitions, etc. are in Appendix C.
(b) Differencing and Detrending
Standard econometric tests, including those used in VAR analysis, assume that the time series used in estimation are stationary; that is, that the mean and variance of the distributions from which the observations are drawn are unchanging through time. This assumption is rarely true for levels of macroeconomic time series. Most series must be made stationary, usually by detrending or differencing, before reliable econometric models can be estimated and tests conducted.
Economists frequently detrend data on the assumption that series have a secular (trend) and a cyclical component. However some recent studies (e.g. Nelson and Plosser (1982)) have suggested that many macroeconomic series may actually have stochastic, rather than deterministic, trends. That is, they may have a “unit root”. In such cases, model residuals do not have the properties needed for valid testing of hypotheses, even if data series are detrended. What is needed, then, is a testing procedure which distinguishes between deterministic time trends and unit roots in data.
Standard asymptotic theory cannot be used to test for unit roots in series which are non-stationary.[3] Fuller (1976) demonstrated that conventional testing procedures will be biased towards accepting stationarity when data are generated by a random-walk-type process. Dickey and Fuller (1979) derive the limiting distributions of the test statistic for the case where the null hypothesis is a unit root, and provide tables of critical values for the test statistic. This test, and two others, developed by Stock and Watson (1988), and Dickey and Pantula (1987) are applied to the series used in the model estimation and testing reported here. Further details of the tests, together with the results, are given in Appendix A.
On the basis of the test results, which suggested the presence of unit roots, all the data on indicators of activity and financial aggregates were first-differenced. The evidence for deterministic trends in addition to unit roots was weaker; hence the tables in the body of this paper report results from models estimated with differenced data only.[4]
For the most part, first-differencing the data is consistent with the approach taken in BMS, where quarterly percentage changes were used for most variables.[5] The exception is that in most of the results reported in this paper, the short-term interest rate has also been differenced, whereas the level was used in BMS.
4. VAR Estimation Results
This section presents results for VAR tests of the relationship between financial indicators and measures of activity. Two measures of activity are used: gross domestic product, and private final demand. The two sets of results are discussed in turn.
Each VAR model includes four lags of each variable. The number of lags was determined by estimating models with eight lags, then using likelihood ratio tests to compare these with models with six or four lags. Neither of the shorter lag specifications were dominated by the eight-lag specification, and so four lags were used for all the causality tests.[6]
(a) Financial Indicators and GDP
This section presents some results, using VAR methodology, for the relationship between GDP, as a measure of activity, and the various financial aggregates and short-term interest rates.
Table 1 shows the results for two-variable VARs, where each financial indicator is compared “one-on-one” with GDP. Both nominal and real GDP are tested. The table shows results over two time periods for the narrow financial aggregates and interest rates: 1969–88, and 1978–88. Tests involving the broader aggregates are restricted to the later period by availability of data.
| 1969:2–1988:3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nom GDP | M1 | Nom GDP | M3 | Nom GDP | Bank lend. | Nom GDP | Bill Rate | ||||
| Nom GDP | 0.371 | 1.548 | Nom GDP | 0.290 | 1.942 | Nom GDP | 0.335 | 2.371 | Nom GDP | 0.947 | 2.275 |
| M1 | 0.570 | 8.036** | M3 | 3.140* | 7.972** | Bank lend. | 3.042* | 13.000** | Bill Rate | 0.412 | 1.142 |
| 1978:1–1988:3 | |||||||||||
| Nom GDP | M1 | Nom GDP | M3 | Nom GDP | Bank lend. | Nom GDP | Bill Rate | ||||
| Nom GDP | 5.769** | 4.943** | Nom GDP | 2.001 | 0.636 | Nom GDP | 3.267* | 1.088 | Nom GDP | 2.557 | 1.842 |
| M1 | 0.852 | 1.862 | M3 | 1.716 | 1.619 | Bank lend. | 0.731 | 5.413** | Bill Rate | 1.055 | 3.024* |
| Nom GDP | Broad money | Nom GDP | AFI lend. | Nom GDP | Credit | ||||||
| Nom GDP | 2.675* | 0.226 | Nom GDP | 1.823 | 0.413 | GDP | 2.776* | 1.370 | |||
| Broad money | 2.534 | 0.688 | AFI lend. | 4.061** | 5.837** | Credit | 2.679* | 7.965 | |||
| 1969:2–1988:3 | |||||||||||
| Real GDP | M1 | Real GDP | M3 | Real GDP | Bank lend. | Real GDP | Bill Rate | ||||
| Real GDP | 1.476 | 1.761 | Real GDP | 1.405 | 0.877 | Real GDP | 1.589 | 1.587 | Real GDP | 1.553 | 0.761 |
| M1 | 0.813 | 8.090** | M3 | 0.922 | 7.839** | Bank lend. | 0.802 | 15.650** | Bill Rate | 0.941 | 1.576 |
| 1978:1–1988:3 | |||||||||||
| Real GDP | M1 | Real GDP | M3 | Real GDP | Bank lend. | Real GDP | Bill Rate | ||||
| Real GDP | 1.380 | 2.082 | Real GDP | 0.878 | 0.860 | Real GDP | 1.917 | 0.812 | Real GDP | 1.405 | 0.981 |
| M1 | 1.340 | 1.732 | M3 | 2.849* | 1.626 | Bank lend. | 1.394 | 3.882* | Bill Rate | 1.496 | 3.108* |
| Real GDP | Broad money | Real GDP | AFI lend. | Real GDP | Credit | ||||||
| Real GDP | 1.181 | 0.378 | Real GDP | 0.919 | 0.360 | Real GDP | 1.193 | 1.030 | |||
| Broad money | 2.853* | 0.622 | AFI lend. | 7.586** | 3.687* | Credit | 6.486** | 5.297** | |||
| 1. Calculated values for F-tests of the hypothesis that the coefficients on lags of explanatory variables are jointly zero. An * denotes significance at the 5 per cent level, ** at the 1 per cent level. Yield curve calculated as 10-year bond rate less 90-day bank bill rate. |
|||||||||||
In interpreting the table, note that the rows of each cell represent the left-hand-side variables in the equation, and the columns represent the right-hand-side variables. The statistics quoted are the computed values of the F-statistic in a test of the hypothesis that lags of the right-hand-side variable are jointly zero in an equation determining the left-hand-side variable. In the top-left-hand cell of Table 1, for example, in an equation explaining growth in nominal GDP by lags of itself and lagged growth of M1, imposing the restriction that coefficients on the lags of nominal GDP are zero yields a test statistic of 0.371, which is below the critical value of 2.5 at the 5 per cent significance level, so that the hypothesis cannot be rejected. Similarly, a test of the hypothesis that lags of M1 have zero coefficients yields a test statistic of 1.548, also insignificant, so that hypothesis cannot be rejected.
In the next row of this cell, lags of nominal GDP do not add much explanatory power to an equation for M1 but lags of M1 itself do. (The test statistic for the latter is 8.036, well outside the critical value.) Clearly, in each cell, the results of most interest are the off-diagonal elements, where the explanation of current values of a variable require more than just the lags of that variable itself.
Interpreting the other cells in Table 1 in like manner suggests the following results:
- both real and nominal GDP tend to lead the broader financial aggregates;
- there is some evidence for GDP leading M3 and bank lending, though this is less consistent; and
- M1 leads nominal GDP in the 1978–88 period.
Table 2 shows results for three-variable VARs, where the bill rate is included in every model. The interpretation of the table is similar to that for Table 1 except that each cell now contains nine entries: the test statistics for the hypothesis of jointly zero coefficients for lags of each of the three variables in each of three equations.
| 1969:2–1988:3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nom GDP | Bill rate | M1 | Nom GDP | Bill rate | M3 | Nom GDP | Bill rate | Bank lend. | |||
| Nom GDP | 0.707 | 2.943* | 2.229 | Nom GDP | 0.386 | 1.379 | 1.078 | Nom GDP | 0.452 | 1.809 | 1.898 |
| Bill rate | 0.570 | 5.601** | 7.066** | Bill rate | 0.602 | 3.489* | 4.624** | Bill rate | 0.796 | 1.665 | 2.424 |
| M1 | 0.759 | 4.596** | 1.734 | M3 | 2.609* | 5.107** | 5.876** | Bank lend. | 1.922 | 1.013 | 13.828** |
| 1978:1–1988:3 | |||||||||||
| Nom GDP | Bill rate | M1 | Nom GDP | Bill rate | M3 | Nom GDP | Bill rate | Bank lend. | |||
| Nom GDP | 5.613** | 1.586 | 4.311** | Nom GDP | .465 | 1.798 | 1.734 | Nom GDP | 3.389* | 2.201 | 1.494 |
| Bill rate | .370 | 4.642** | 2.004 | Bill rate | .961 | 1.816 | 2.712* | Bill rate | 1.467 | 3.004* | 1.816 |
| M1 | .889 | 1.880 | 0.558 | M3 | 1.912 | 16.941** | 1.733 | Bank lend. | 0.844 | 0.245 | 4.500** |
| Nom GDP | Bill rate | Broad money | Nom GDP | Bill rate | AFI lend. | Nom GDP | Bill rate | Credit | |||
| Nom GDP | 2.934* | 2.350 | 0.812 | Nom GDP | 1.730 | 1.349 | 0.126 | Nom GDP | 2.290 | 1.258 | 0.859 |
| Bill rate | 1.459 | 5.403** | 4.222** | Bill rate | 2.033 | 2.927* | 1.775 | Bill rate | 2.051 | 3.375* | 2.658 |
| Broad money | 1.872 | 3.322* | 1.055 | AFI lend. | 2.936* | 1.516 | 4.912** | Credit | 3.757* | 1.775 | 9.460** |
| 1969:2–1988:3 | |||||||||||
| Real GDP | Bill rate | M1 | Real GDP | Bill rate | M3 | Real GDP | Bill rate | Bank lend. | |||
| Real GDP | 1.484 | 0.879 | 1.831 | Real GDP | 1.233 | 0.658 | 0.767 | Real GDP | 1.469 | 0.268 | 1.026 |
| Bill rate | 0.154 | 5.350** | 5.828** | Bill rate | 0.911 | 4.101** | 4.387** | Bill rate | 0.908 | 2.402 | 1.999 |
| M1 | 0.867 | 4.445** | 2.020 | M3 | 0.956 | 5.613** | 9.081** | Bank lend. | 1.263 | 2.452 | 19.048** |
| 1978:1–1988:3 | |||||||||||
| Real GDP | Bill rate | M1 | Real GDP | Bill rate | M3 | Real GDP | Bill rate | Bank lend. | |||
| Real GDP | 1.402 | 0.659 | 1.606 | Real GDP | 0.893 | 0.607 | 0.504 | Real GDP | 1.922 | 1.375 | 1.217 |
| Bill rate | .500 | 4.393** | 1.735 | Bill rate | 0.774 | 3.470* | 1.164 | Bill rate | 1.226 | 2.831* | 1.167 |
| M1 | 1.598 | 2.167 | 0.276 | M3 | 3.367* | 0.963 | 1.886 | Bank lend. | 1.340 | 0.155 | 3.209* |
| Real GDP | Bill rate | Broad money | Real GDP | Bill rate | AFI lend. | Real GDP | Bill rate | Credit | |||
| Real GDP | 1.493 | 0.990 | 0.450 | Real GDP | 1.114 | 0.707 | 0.170 | Real GDP | 1.019 | 0.784 | 0.827 |
| Bill rate | 0.748 | 4.407** | 2.816* | Bill rate | 1.891 | 2.178 | 1.233 | Bill rate | 1.829 | 2.872* | 1.984 |
| Broad money | 2.644 | 3.885* | 0.747 | AFI lend. | 5.672** | 1.385 | 1.965 | Credit | 7.347** | 1.626 | 5.567** |
| 1. Calculated values for F-tests of the hypothesis that the coefficients on lags of explanatory variables are jointly zero. An * denotes significance at the 5 per cent level, ** at the 1 per cent level. |
|||||||||||
Results here are similar to those for the two-variable models: GDP tends to lead AFI lending and credit, and also M3, though again the latter result is not as consistent: it occurs only on half the occasions on which M3 enters. There is one instance of the bill rate leading nominal GDP, and one of M1 leading nominal GDP, but overall there is not strong evidence of “Granger-causality” in these cases.
There are a number of instances of complex relationships between the bill rate and the financial aggregates, where lags of the aggregate help explain the bill rate and vice versa.
Appendix B contains results for the same tests based on data which are not seasonally adjusted. Similar conclusions are evident: the broad lending and credit aggregates tend to be led by GDP, and there is two-way dynamic interaction between the bill rate and the financial aggregates in a number of cases.
(b) Financial Indicators and Private Final Demand
The principal activity indicator in BMS was private final demand. This section presents results of tests parallel to those in Section 4(a), but using PFD as the activity indicator. The interpretation of Tables 3 and 4 is analogous to that of the earlier tables.
| 1969:2–1988:3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nom PFD | M1 | Nom PFD | M3 | Nom PFD | Bank lend. | Nom PFD | Bill Rate | ||||
| Nom PFD | 3.781** | 1.725 | Nom PFD | 3.330* | 0.879 | Nom PFD | 3.896** | 0.738 | Nom PFD | 5.772** | 0.351 |
| M1 | 1.084 | 6.311** | M3 | 1.419 | 6.022** | Bank lend. | 0.970 | 13.218** | Bill Rate | 1.256 | 1.778 |
| 1978:1–1988:3 | |||||||||||
| Nom PFD | M1 | Nom PFD | M3 | Nom PFD | Bank lend. | Nom PFD | Bill Rate | ||||
| Nom PFD | 1.196 | 1.815 | Nom PFD | 1.969 | 1.871 | Nom PFD | 2.626 | 1.197 | Nom PFD | 2.133 | 0.100 |
| M1 | 1.831 | 1.785 | M3 | 1.142 | 1.882 | Bank lend. | 0.670 | 4.955** | Bill Rate | 2.875* | 3.669* |
| Nom PFD | Broad money | Nom PFD | AFI lend. | Nom PFD | Credit | ||||||
| Nom PFD | 2.628 | 2.063 | Nom PFD | 2.882* | 0.730 | PFD | 2.403 | 0.230 | |||
| Broad money | 2.507 | 1.253 | AFI lend. | 2.119 | 3.692* | Credit | 1.011 | 7.389** | |||
| 1969:2–1988:3 | |||||||||||
| Real PFD | M1 | Real PFD | M3 | Real PFD | Bank lend. | Real PFD | Bill Rate | ||||
| Real PFD | 1.178 | 1.257 | Real PFD | 1.634 | 0.882 | Real PFD | 1.988 | 1.734 | Real PFD | 2.501 | 1.377 |
| M1 | 2.431 | 5.323** | M3 | 2.266 | 6.705** | Bank lend. | 0.499 | 14.670** | Bill Rate | 5.081** | 3.629** |
| 1978:1–1988:3 | |||||||||||
| Real PFD | M1 | Real PFD | M3 | Real PFD | Bank lend. | Real PFD | Bill Rate | ||||
| Real PFD | 1.085 | 1.255 | Real PFD | 2.234 | 1.087 | Real PFD | 2.532 | 0.977 | Real PFD | 2.335 | 0.098 |
| M1 | 3.389* | 2.378 | M3 | 0.934 | 1.741 | Bank lend. | 1.170 | 4.519** | Bill Rate | 3.198* | 3.971** |
| Real PFD | Broad money | Real PFD | AFI lend. | Real PFD | Credit | ||||||
| Real PFD | 1.924 | 2.561 | Real PFD | 2.742* | 1.596 | Real PFD | 2.700* | 1.152 | |||
| Broad money | 3.035* | 1.281 | AFI lend. | 4.929** | 1.335 | Credit | 2.306 | 4.033** | |||
| 1. Calculated values for F-tests of the hypothesis that the coefficients on lags of explanatory variables are jointly zero. An * denotes significance at the 5 per cent level, ** at the 1 per cent level. | |||||||||||
| 1969:2–1988:3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nom PFD | Bill rate | M1 | Nom PFD | Bill rate | M3 | Nom PFD | Bill rate | Bank lend. | |||
| Nom PFD | 3.054* | 0.233 | 1.520 | Nom PFD | 3.093* | 0.328 | 0.825 | Nom PFD | 2.096* | 0.501 | 1.001 |
| Bill Rate | 0.298 | 5.710** | 5.643** | Bill rate | 0.438 | 3.887** | 3.478** | Bill rate | 0.662 | 2.316 | 1.541 |
| M1 | 1.093 | 4.408** | 1.543 | M3 | 1.441 | 5.631** | 5.975** | Bank lend. | 0.930 | 1.877 | 14.392** |
| 1978:1–1988:3 | |||||||||||
| Nom PFD | Bill rate | M1 | Nom PFD | Bill rate | M3 | Nom PFD | Bill rate | Bank lend. | |||
| Nom PFD | 1.018 | 0.610 | 2.227 | Nom PFD | 1.267 | 0.135 | 1.707 | Nom PFD | 2.291 | 0.243 | 1.123 |
| Bill Rate | 0.764 | 4.170** | 0.883 | Bill rate | 1.671 | 3.689* | 0.939 | Bill rate | 3.208* | 3.935* | 1.845 |
| M1 | 1.063 | 1.166 | 0.754 | M3 | 0.868 | 0.171 | 1.545 | Bank lend. | 0.618 | 0.085 | 4.028** |
| Nom PFD | Bill rate | Broad money | Nom PFD | Bill rate | AFI lend. | Nom PFD | Bill rate | Credit | |||
| Nom PFD | 1.801 | 0.537 | 2.372 | Nom PFD | 2.366 | 0.110 | 0.667 | Nom PFD | 2.057 | 0.190 | 0.306 |
| Bill Rate | 1.608 | 5.191** | 2.510 | Bill rate | 2.680 | 3.411* | 0.819 | Bill rate | 2.735* | 3.633* | 1.643 |
| Broad monev | 1.328 | 2.719* | 1.363 | AFI lend. | 1.486 | 1.682 | 4.323** | Credit | 1.200 | 0.925 | 7.737** |
| 1969:2–1988:3 | |||||||||||
| Real PFD | Bill rate | M1 | Real PFD | Bill rate | M3 | Real PFD | Bill rate | Bank lend. | |||
| Real PFD | 1.336 | 0.845 | 0.736 | Real PFD | 1.834 | 0.918 | 0.463 | Real PFD | 1.975 | 1.203 | 1.377 |
| Bill Rate | 1.834 | 6.662** | 3.576* | Bill rate | 4.655** | 6.471** | 4.230** | Bill rate | 5.022** | 4.904** | 2.244 |
| M1 | 1.370 | 3.303* | 2.098* | M3 | 1.555 | 4.816** | 8.382** | Bank lend. | 1.052 | 2.467 | 16.943** |
| 1978:1–1988:3 | |||||||||||
| Real PFD | Bill rate | M1 | Real PFD | Bill rate | M3 | Real PFD | Bill rate | Bank lend. | |||
| Real PFD | 1.060 | 0.154 | 1.184 | Real PFD | 1.896 | 0.071 | 0.942 | Real PFD | 2.291 | 0.156 | 0.939 |
| Bill Rate | 0.999 | 4.260** | 0.883 | Bill rate | 1.798 | 4.029** | 0.820 | Bill rate | 2.774* | 3.964* | 1.219 |
| M1 | 3.003* | 1.737 | 1.514 | M3 | 0.773 | 0.251 | 1.356 | Bank lend. | 1.482 | 0.459 | 4.552** |
| Real PFD | Bill rate | Broad money | Real PFD | Bill rate | AFI lend. | Real PFD | Bill rate | Credit | |||
| Real PFD | 1.330 | 0.489 | 2.778 | Real PFD | 2.285 | 0.047 | 1.361 | Real PFD | 2.440 | 0.161 | 1.100 |
| Bill Rate | 1.754 | 5.783** | 2.390 | Bill rate | 2.323 | 3.563* | 0.306 | Bill rate | 2.067 | 3.595* | 0.811 |
| Broad money | 1.798 | 2.771* | 1.311 | AFI lend. | 4.362** | 2.085 | 1.754 | Credit | 2.647 | 1.149 | 4.609** |
| 1. Calculated values for F-tests of the hypothesis that the coefficients on lags of explanatory variables are jointly zero. An * denotes significance at the 5 per cent level, ** at the 1 per cent level. | |||||||||||
There is some support for the hypothesis that activity leads the broad aggregates, though it is not as strong as where GDP is used as the activity variable.
On a number of occasions lags of growth in PFD explain changes in the bill rate. This result is in apparent contrast to the conclusions of BMS, and some reconciliation is in order.
First, it is notable that in the three-variable models, the result occurs five times, and four of these are when bank lending is the third variable. In the thirteen sets of results in Table 4 which do not include bank lending, PFD leads the bill rate only once (when M3 is included). This suggests that perhaps there is some unique feature of the interaction of interest rates, PFD and bank lending which is reflected in the results.
Second, the result that PFD leads the bill rate hinges, to some extent, on the specification of the interest rate series in the present paper as a first difference, rather than as a level as in BMS. When the two-variable VAR tests in Table 3 are conducted with the level, rather than the change, of the bill rate, a unidirectional relationship between PFD and the bill rate can no longer be established.
5. The External Sector
To this point, the discussion has focussed on the interaction of the financial system and domestic economic activity. In this section, the scope is broadened, to allow explicitly for external linkages.
In an open economy, the impact of monetary policy comes partly through the exchange rate. Most treatments of this begin with some sort of interest-parity condition:
where it is the interest rate at time t,  is the foreign interest
rate of equivalent maturity, e is the log of the exchange rate and E( ) and
d denote, respectively, the expectations (conditional on information available
at time t) and difference operators.
is the foreign interest
rate of equivalent maturity, e is the log of the exchange rate and E( ) and
d denote, respectively, the expectations (conditional on information available
at time t) and difference operators.
This condition says that properly-functioning financial markets keep the domestic interest rate aligned with the foreign rate (assumed to be exogenous), allowing for expected changes in the exchange rate over the relevant period. A change in monetary policy which alters the domestic interest rate will, other things equal, alter the exchange rate so as to preserve the equality of exchange rate-adjusted expected returns across countries. For example, higher domestic interest rates will, other things equal, result in an instantaneous appreciation of the exchange rate so as to generate an expected depreciation of the exchange rate back towards the given “fundamental” level, which will offset the interest differential over the life of the asset. Were this not so, opportunities would exist to make large expected profits.
Now there are some practical difficulties with equation (5), mainly because other things will not always be equal. For example, the behaviour of risk-averse market participants may allow deviations from interest parity to occur. Indeed, there is good reason to suppose that there is an additional term driving a wedge between foreign and domestic rates, representing a currency risk premium.[7] As long as this premium is constant, then the statements made above about monetary policy changes still hold. But if the premium varies through time, then this approach, as it stands, is not entirely adequate.
In addition, a change in domestic interest rates may come at a time when “fundamental” factors in the economy are causing a reassessment of expectations about the likely course of the exchange rate. This may make a clear connection between changes in monetary policy and the exchange rate difficult to observe in practice.
Nevertheless, it seems a reasonable starting point for analysis to accept that a change in domestic monetary policy will have implications for the exchange rate, and therefore for those sectors of the economy which are sensitive to exchange rate changes. Under this maintained hypothesis, the channels through which such effects might be observed are the price elasticities of demand and supply for imports and exports. A tightening of domestic monetary policy, for example, will tend to raise the exchange rate and lower the domestic currency price of tradeable goods. This will encourage the substitution of imported for domestically produced goods in domestic expenditure, discourage the production of domestically produced tradeables both for domestic consumption and export, and discourage absorption of Australian exports by the rest of the world. In testing for these channels empirically, it will also be necessary to control for domestic and foreign price developments, since it is the real exchange rate which is important, and changes in foreign and domestic absorption.[8]
The other part of the story, of course, is that a rise in domestic interest rates should also reduce domestic expenditure and incomes, and therefore imports (especially as business investment, usually thought to be interest-sensitive, has a high imported component). There are therefore two effects of a change in monetary policy on the real trade balance, which operate in different directions. The empirical tests will therefore need to control for changes in private domestic expenditure.
This section uses VAR models to look at some of these channels. The first set of models includes real GDP, the bill rate, one monetary aggregate, the trade-weighted index of the Australian dollar, a term representing the difference between foreign and domestic prices (PDIFF, the log difference between the GDP deflators for Australia and the major seven OECD economies) and private expenditure in the major seven OECD economies (M7PFD).
The second set of VAR models includes exports instead of GDP. The third set of models includes imports and real PFD rather than the bill rate.
As in Section 4, all the models use variables in log-differences, apart from the bill rate which is simply differenced.[9] The availability of OECD data restricted the sample period to 1972:2–1988:2, which imposed a fairly tight constraint on degrees of freedom. With respect to financial aggregates, we confined attention to M1 and M3, since there are really too few observations available on the broader aggregates to estimate these large models.
The results are presented in Table 5. The interpretation of these is similar to that of the earlier tables. Results are presented using both M1 and M3 as the monetary aggregate.
| 1972:2–1988:2 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Real GDP | Bill rate | M1 | TWI | PDIFF | M7PFD | Real GDP | Bill rate | M3 | TWI | PDIFF | M7PFD | ||
| Real GDP | 3.413* | 0.477 | 1.891 | 0.911 | 1.725 | 2.077 | Real GDP | 2.806* | 0.419 | 0.644 | 0.858 | 2.014 | 2.091 |
| Bill rate | 0.505 | 5.611** | 3.215* | 1.333 | 1.799 | 1.400 | Bill rate | 1.321 | 5.577** | 4.183** | 2.504 | 2.435 | 1.412 |
| M1 | 1.001 | 2.817* | 1.126 | 1.644 | 0.128 | 1.674 | M3 | 1.390 | 2.192 | 4.315** | 1.409 | 0.961 | 0.757 |
| TWI | 1.170 | 1.286 | 1.606 | 1.260 | 0.388 | 0.562 | TWI | 1.665 | 2.421 | 1.899 | 2.249 | 0.502 | 0.853 |
| PDIFF | 0.944 | 3.065* | 0.489 | 1.084 | 2.408 | 2.666* | PDIFF | 0.739 | 1.252 | 1.314 | 0.787 | 2.011 | 1.967 |
| M7PFD | 1.185 | 0.803 | 1.267 | 0.888 | 3.911** | 1.904 | M7PFD | 0.848 | 0.992 | 0.824 | 0.859 | 3.241* | 1.547 |
| 1972:2–1988:2 | |||||||||||||
| Real Xpts | Bill rate | M1 | TWI | PDIFF | M7PFD | Real Xpts | Bill rate | M3 | TWI | PDIFF | M7PFD | ||
| Real Xpts | 0.622 | 0.447 | 2.168 | 2.940* | 0.049 | 0.917 | Real Xpts | 1.508 | 0.094 | 0.512 | 2.003 | 0.201 | 0.667 |
| Bill rate | 1.902 | 5.731** | 5.455** | 1.613 | 2.331 | 0.993 | Bill rate | 2.314 | 6.213** | 5.926** | 2.747* | 3.856** | 1.441 |
| M1 | 1.216 | 1.788 | 1.517 | 2.399 | 0.222 | 1.686 | M3 | 0.978 | 1.529 | 5.877** | 1.471 | 1.072 | 0.893 |
| TWI | 1.782 | 2.087 | 2.067 | 0.833 | 0.540 | 0.769 | TWI | 1.502 | 2.304 | 1.566 | 1.330 | 0.615 | 0.626 |
| PDIFF | 2.625* | 4.145** | 1.674 | 2.196 | 2.828* | 3.695* | PDIFF | 1.674 | 1.396 | 1.867 | 1.129 | 2.294 | 2.297 |
| M7PFD | 0.874 | 0.845 | 0.591 | 0.778 | 3.176* | 2.189 | M7PFD | 1.018 | 1.123 | 0.629 | 0.889 | 2.691* | 1.771 |
| 1972:2–1988:2 | |||||||||||||
| Real Mpts | Real PFD | M1 | TWI | PDIFF | M7PFD | Real Mpts | Real PFD | M3 | TWI | PDIFF | M7PFD | ||
| Real Mpts | 0.820 | 2.097 | 2.438 | 2.989* | 1.666 | 1.166 | Real Mpts | 0.987 | 2.891* | 2.707* | 2.885* | 1.967 | 1.276 |
| Real PFD | 0.366 | 0.795 | 0.527 | 0.655 | 0.619 | 0.965 | Real PFD | 0.483 | 1.024 | 1.242 | 1.610 | 0.977 | 1.297 |
| M1 | 1.726 | 2.094 | 2.699* | 2.099 | 2.111 | 1.399 | M3 | 2.540 | 2.212 | 2.363 | 1.784 | 3.385* | 2.892* |
| TWI | 0.471 | 0.208 | 1.337 | 0.603 | 0.390 | 0.778 | TWI | 1.197 | 0.655 | 1.057 | 0.962 | 1.277 | 0.850 |
| PDIFF | 3.349* | 2.530 | 2.229 | 0.888 | 1.991 | 3.306* | PDIFF | 3.531* | 1.441 | 4.993** | 0.452 | 1.566 | 1.825 |
| M7PFD | 1.677 | 0.622 | 0.577 | 0.189 | 2.913* | 3.668* | M7PFD | 1.539 | 0.328 | 0.456 | 0.058 | 1.679 | 3.780* |
| 1. Calculated values for F-tests of the hypothesis that the coefficients on lags of explanatory variables are jointly zero. An * denotes significance at the 5 per cent level, ** at the 1 per cent level. | |||||||||||||
The first panel shows results for models including real GDP and the range of financial and foreign variables. There is no evidence of Granger-causality from any of the other variables to GDP. There is evidence again of a dynamic relationship between the monetary aggregates and the bill rate (the test statistics for lags of M1 or M3 affecting the bill rate are significant at the 5 per cent level or less, and the statistics for the reverse relationship would be significant at levels only slightly higher than the 5 per cent level used as the critical value in the tables).
In the second panel of the table, real exports of goods and services replaces GDP. When the price differential and foreign absorption are controlled, lags of the TWI are significant in explaining exports in the equation with M1. M1 and M3 again help explain the bill rate, though the reverse is not true in this case.
In the third panel, real imports of goods and services is the activity variable, and real private final demand replaces the bill rate. The TWI is significant in explaining imports. Real PFD is also significant when included with M3 (and would be significant at the 10 per cent level with M1). M3 also helps in explaining imports.
There also appears to be a relationship between the price differential and M7PFD. In five out of six models, lags of PDIFF help explain M7PFD, and the reverse is true in three out of six cases. Given the definition of PDIFF, this could be interpreted as a proxy for effects of changes in the major countries' terms of trade on absorption in those countries. In only one instance does M7PFD have a significant relationship with a variable other than itself or PDIFF.[10]
One important point in all this is that while the discussion of the external-sector impacts of changes in monetary policy was motivated in a floating exchange rate context, the long sample period required by the VAR techniques (because of the number of parameters to be estimated) covers more than just the floating rate period. It also covers the period of fixed exchange rates (although the parities were altered in this period) until November 1976, and the crawling peg from then until December 1983.
Of course changes in the exchange rate, under whatever regime, would still be expected to have subsequent developments on the economy, but the dynamic interaction between monetary policy, the exchange rate and the economy may differ between exchange rate regimes.
Accordingly, the results in this section should be regarded as quite preliminary. That said, the results do suggest that there is some evidence of both exchange rate and expenditure effects on components of the real trade balance. The relative size and timing of these effects is, naturally, a separate question.
6. Conclusions
On the basis of the results, there is further support for the notion that measures of economic activity lead the broader lending/credit aggregates, which was an important conclusion of BMS. No consistent leading or lagging relationship for the narrower aggregates could be found using this methodology.
The other important conclusion drawn tentatively in BMS, was that the level of short-term interest rates was consistently related to movements in economic activity, with a lag, in episodes of changing interest rates.
There is no strong statistical support for this proposition on the basis of the techniques used here. BMS found a strong negative correlation between the level of the bill rate and subsequent growth in PFD. Equally, a simple linear regression of PFD on lags of the bill rate would reveal significant negative coefficients. But the tests in the present paper look for that information to be found after past values of PFD itself are included; this is a more difficult test to pass.
It is noteworthy that while BMS observed that each major period of weakness in PFD was preceded by a big rise in the bill rate, that rise in turn came during a period of very strong growth in PFD: “boom” conditions provoked rising interest rates. In addition, the bill rate kept rising for a quarter or two after the growth of PFD initially slowed. A possible reconciliation of the observations of BMS with the results in the present paper is that interest rates responded, partly through market forces, but at least partly because of a monetary policy reaction as well, to the growth of domestic demand, and in so doing affected the subsequent growth of the economy. Part of that reconciliation would also have to be that monetary policy changed course only when it was clear that the economy had already done so. In that case, tests such as those employed in this paper would be unlikely to support a view that interest rates are “exogenous” in a statistical sense. Nor would there be much hope for finding precise estimates of the response of the economy to monetary policy changes, at least using these techniques, since policy changes themselves are related to earlier developments in the economy, and effects may be limited only to changes greater than some (unknown) threshold.
A disentanglement of these processes is probably required for a full understanding of the effect of monetary policy on the economy. In principle, techniques with very general lag structures, such as those in this paper, should allow something to be said about two-way “causation”. The fact that the results here do not allow much to be said may indicate that the responses are not systematic – the lags both in changing monetary policy and in its taking effect may be variable – or that the world does not work in linear fashion. At the very least, it suggests that the structure underlying the reduced forms that make up the VARs is not well understood.
Under the maintained hypothesis that the exchange rate and short-term domestic interest rates are linked through an interest-parity condition, the results of Section 5 are consistent with a monetary policy effect on the trade sector through the exchange rate, though again it should be emphasised that these results are only preliminary in nature. Little can be said about the size and speed of this effect compared with that operating on the trade balance (in the opposite direction) through domestic expenditure. This is an important question, however, and should be the subject of continued research.
Appendix A: Tests for Unit Roots and Time Trends
These tests are typically based on an equation of the form:
The null hypothesis is that there is a unit root in y – i.e. that δ = 0. Tests of this hypothesis frequently involve comparing the computed values from the above equation with appropriate critical values (e.g. the, t-statistic for δ is the test-statistic in the Dickey-Fuller test).
If δ = 0, µ ≠ 0, there is a unit root “with drift”; if β ≠ 0, there is a time trend.
Tables A1, A2 and A3 report results of Dickey-Pantula (DP), Stock-Watson (SW) and Dickey-Fuller (DF) tests for the likely presence of two or less unit roots under a series of nested hypotheses on deterministic trends. (The test statistics were computed using a program developed by Dr Rob Trevor.) All variables except interest rates are tested in natural log form.
| Variable | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Test | Real PFD | Real GDP | Nom PFD | Nom GDP | M1 | M3 | Bank lend. | Broad Money | AFI lend | Credit | |
| Two unit roots vs. at most one | |||||||||||
| T | −2.742 ** | −1.781 + | 0.373 | 0.201 | 0.236 | −0.298 | 0.465 | −1.151 | 0.919 | 1.476 | |
| DP | −6.969** | −3.142+ | −3.200+ | −2.815 | −3.484* | −3.299+ | −3.066 | −3.416* | −3.379+ | −2.235 | |
| SW | −119.120** | −95.409** | −64.411** | −91.491** | −41.129** | −34.800** | −24.820* | −33.588** | −17.073 | −16.143 | |
| DF | −5.120** | −3.313+ | −2.544 | −2.675 | −3.920* | −3.182+ | −2.480 | −2.708 | −2.942 | −2.575 | |
| Constant | 4.701 ** | 3.169 ** | 3.365 ** | 3330 ** | 3.718 ** | 2.788 ** | 2.655 ** | 2.761 ** | 2.684 ** | 2.343 * | |
| DP | −5.632** | −2.714+ | −3.357* | −3.024* | −3.503** | −3.336* | −3.029* | −3.252* | −3.111* | −1.740 | |
| SW | −117.880** | −93.885** | −58.904** | −87.604** | −40.883** | −34.723** | −24.082** | −33.362** | −16.275* | −12.719 | |
| DF | −4.323** | −2.905* | −2.785+ | −2.907* | −3.942** | −3.212* | −2.457 | −2.454 | −2.784v | −2.074 | |
| One unit root vs. none | |||||||||||
| T2 | −2.810 ** | 0.771 | −1.506 | −1.247 | −1.818 + | −2.227 * | −1.251 | −2.974 ** | 2.286 * | 2.570* | |
| SW | −24.096 | −7.276 | −3.408 | −4.680 | −12.182 | −10.634 | −8.592 | −15.137 | −8.224 | −6.818 | |
| T | 1.475 | 2.386 * | 1.876 + | 1.842 + | 2.377* | 2.290* | 2.893** | 2.358 * | 1.822 + | 1.152 | |
| DP | −1.165 | −2.804 | −1.744 | −1.869 | −2.227 | −2.262 | −2.220 | −1.196 | −0.342 | −0.747 | |
| SW | −4.508 | −6.607 | −5.286 | −6.044 | −9.800 | −8.914 | −8.052 | −7.140 | −5.402 | −2.464 | |
| DF | −1.602 | −2.785 | −1.822 | −1.846 | −2.365 | −2.852 | −2.628 | −1.870 | −1.462 | −0.612 | |
| Constant | 2.954 ** | 2.436 * | 0.810 | 0.920 | 0.455 | 1.085 | 0.479 | 1.474 | −0.113 | −0.681 | |
| DP | −3.773** | −2.080 | 0.268 | −0.050 | 0.081 | −0.241 | 0.462 | −1.149 | 1.262 | 1.335 | |
| SW | −0.995 | −1.135 | 0.072 | 0.024 | 0.027 | −0.141 | 0.112 | −0.147 | 0.153 | 0.302 | |
| DF | −2.973* | −2.303 | 0.204 | 0.052 | 0.072 | −0.437 | 0.311 | −1.201 | 0.866 | 1.434 | |
| 1. An * (**) (+) indicates rejection of the null hypothesis that the coefficient is zero at the one (five) (ten) per cent level. For T2, T, and constant, the null is that the coefficient on the trend or drift term is zero. For the other tests the null is that there are two, or one, unit roots. | |||||||||||
| Variable | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Test | Real PFD | Real GDP | Nom PFD | Nom GDP | M1 | M3 | Bank lend. | Broad Money | AFI lend | Credit |
| Two unit roots vs. at most one | ||||||||||
| T | −2.790 ** | −2.618 ** | 0.489 | 0.494 | 0.283 | 0.071 | 0.420 | −1.132 | 0.831 | 1.393 |
| DP | −5.307** | −4.091** | −2.656 | −2.720 | −2.744 | −2.366 | −2.325 | −2.804 | −2.428 | −1.997 |
| SW | −161.900** | −144.180** | −163.660** | −139.550** | −65.158** | −57.648** | −61.208** | −42.167** | −31.195** | −30.395** |
| DF | −7.7631** | −5.790** | −4.071** | −3.744* | −4.370** | −3.342+ | −2.838 | −3.584* | −2.962 | −2.955 |
| Constant | 4.979** | 4.048** | 4.063** | 3.953** | 5.094** | −3.863** | 2.652** | 2.588** | 2.901** | 2.210* |
| DP | −4.294** | −3.275* | −2.904* | −2.923* | −2.755+ | −2.401 | −2.303 | −2.375 | −2.297 | −1.513 |
| SW | −162.140** | −144.180** | −163.630** | −139.310** | −65.134** | −57.530** | −60.406** | −42.444** | −30.536** | −26.140** |
| DF | −6.575** | −4.832** | −4.177** | −3.830** | −4.392** | −3.370* | −2.816+ | −3.199* | −2.837+ | −2.357 |
| One unit root vs. none | ||||||||||
| T2 | −3.284 ** | −0.682 | −0.636 | −0.957 | −2.225 * | −2.432 * | −1.185+ | −3.850 ** | 2.122 * | 2.888*** |
| SW | −135.250** | −110.770** | −35.398* | −52.909** | −15.555 | −13.327 | −8.926 | −27.447+ | −8.168 | −7.439 |
| T | 2.143 * | 1.449 | 1.654 + | 1.833 + | 2.649 ** | 2.339 * | 2.574* | 2.484 * | 1.652 + | 0.602 |
| DP | −1.522 | −1.975 | −1.803 | −1.944 | −2.805 | −3.159+ | −2.974 | −1.158 | −1.546 | −0.566 |
| SW | −62.560** | −66.172** | −26.435* | −43.733** | −12.628 | −10.431 | −8.336 | −12.142 | −5.635 | −2.136 |
| DF | −1.823 | −1.859 | −1.645 | −1.801 | −1.893 | −2.121 | −2.635 | −1.578 | −1.391 | −0.429 |
| Constant | 2.828 ** | 3.057 ** | 1.066 | 0.931 | 0.377 | 0.938 | 0.482 | 1.272 | −0.062 | −0.807 |
| DP | −3.139* | −2.774+ | −0.049 | −0.064 | 0.089 | −0.418 | 0.255 | −1.451 | 0.796 | 1.273 |
| SW | −1.469 | −3.229 | 0.087 | 0.049 | 0.044 | −0.044 | 0.096 | −0.161 | 0.133 | 0.314 |
| DF | −3.055* | −2.953* | 0.336 | 0.347 | 0.148 | −0.179 | 0.262 | −1.179 | 0.779 | 1.362 |
| 1. An*(**) (+) indicates rejection of the null hypothesis that the coefficient is zero at the one (five) (ten) per cent level. For T2, T, and constant, the null is that the coefficient on the trend or drift term is zero. For the other tests the null is that there are two, or one, unit roots. | ||||||||||
| Variable | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Test | Real Mpts | Real Xpts | Nom Mpts | Nom Xpts | Bill rate | TWI | GDP Def. | PDIFF | M7PFD |
| Two unit roots vs. at most one | |||||||||
| T | −0.866 | 0.040 | 0.235 | 0.976 | −0.172 | −0.895 | 0.026 | −0.352 | 0.306 |
| DP | −6.458** | −4.902** | −5.342** | −4.991** | −3.890* | −3.494* | −1.874 | −1.839 | −2.770 |
| SW | −74.813** | −115.750** | −78.767** | −104.060** | −79.569** | −98.801** | −64.220** | −74.390** | −45.300** |
| DF | −5.445** | −4.785** | −4.973** | −4.532** | −4.898** | −4.112** | −1.966 | −1.786 | −2.415 |
| Constant | 3.301 ** | 3.657 ** | 4.178 ** | 4.165 ** | 0.621 | −0.728 | 1.723 + | 2.072 * | 2.062 * |
| DP | −6.334** | −4.936** | −5.404** | −4.809** | −3.922** | −3.303* | −1.886 | −1.836 | −2.895* |
| SW | −74.688** | −115.780** | −78.109** | −103.000** | −79.482** | −95.481** | −60.358** | −74.358** | −44.900** |
| DF | −5.374** | −4.819** | −5.062** | −4.427** | −4.945** | −3.892** | −1.969 | −1.785 | −2.545 |
| One unit root vs. none | |||||||||
| T2 | −1.019 | −1.016 | 0.390 | −0.361 | −1.529 | −3.317 ** | −1.143 | 2.118* | 0.646 |
| SW | −24.632+ | −25.561+ | −8.731 | −12.474 | −27.270+ | −17.458 | −5.009 | −6.829 | −7.054 |
| T | 3.882 ** | 1.976 | 1.919 + | 2.496 * | 3.941 ** | −2.063 * | −3.987 ** | 2.437 * | −2.704 ** |
| DP | −3.169+ | −1.806 | −1.606 | −2.353 | −4.008** | −1.519 | −3.561* | −3.525* | −2.449 |
| SW | −21.303+ | −20.138+ | −7.166 | −11.390 | −25.596* | −7.040 | −5.570 | −7.868 | −8.256 |
| DF | −3.993** | −1.944 | −1.821 | −2.377 | −3.753* | −2.099 | −3.837* | −2.943 | −2.852 |
| Constant | 1.660 + | 0.560 | 0.893 | 0.280 | 1.969 * | 1.539 | 1.054 | 0.414 | 0.162 |
| DP | −1.688 | −0.353 | 0.346 | 1.014 | −1.395 | −0.571 | −0.099 | −0.974 | −0.235 |
| SW | −1.566 | −0.276 | 0.001 | 0.282 | −7.109 | −1.965 | −0.237 | −1.187 | −0.091 |
| DF | −1.516 | −0.360 | −0.019 | 0.711 | −1.533 | −1.087 | −0.347 | −1.006 | −0.086 |
| 1. An * (**) (+) indicates rejection of the null hypothesis that the coefficient is zero at the one (five) (ten) per cent level. For T2, T, and constant, the null is that the coefficient on the trend or drift term is zero. For the other tests the null is that there are two, or one, unit roots. | |||||||||
The interpretation of the tables is as follows. The first row of figures gives the test statistic for the null hypothesis that there is no time trend in a model which assumes two unit roots. A significant value then leads to the first set of unit root tests immediately below. Here the null is that two unit roots exist. Significant values lead to a rejection of the hypothesis. If the statistic in the ‘T’ row is not significant, the null of no time trend is accepted, and the next test is to see whether the constant, or “drift” term, is significant. If so, the “two unit roots with drift” hypothesis can be tested with the next set of statistics. Significant statistics here mean a rejection of the null hypothesis. If the hypothesis of two unit roots is rejected, the next step is to assess the hypothesis of a single unit root, using an analogous procedure, in the lower half of the table.
The results suggest that all the time series have at least one unit root, indicating the need for first-differencing. The evidence on the trend components of the series is mixed, and generally weak, but several series may have first or second-order time trends.
Appendix B: Tests Using Alternative Data
The first four tables in this Appendix duplicate the tests reported in Tables 1 to 4 in the main paper, except that the data are not seasonally adjusted. Seasonality is captured by including seasonal dummies in the regression equations.
Tables B1 and B2 show results using GDP as the activity variable. Compared with the results in the main paper, the principal difference is that there are no cases of GDP leading M3 or bank lending. There is still support for GDP leading the broader aggregates, though not as strong as in the seasonally adjusted case.
| 1969:2–1988:3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nom GDP | M1 | Nom GDP | M3 | Nom GDP | Bank lend. | Nom GDP | Bill Rate | ||||
| Nom GDP | 2.418 | 1.205 | Nom GDP | 2.449 | 1.527 | Nom GDP | 2.279 | 1.510 | Nom GDP | 1.576 | 1.127 |
| M1 | 1.648 | 3.594* | M3 | 1.382 | 3.924** | Bank lend. | 0.698 | 6.552** | Bill Rate | 0.719 | 0.044 |
| 1978:1–1988:3 | |||||||||||
| Nom GDP | M1 | Nom GDP | M3 | Nom GDP | Bank lend. | Nom GDP | Bill Rate | ||||
| Nom GDP | 4.637** | 4.186** | Nom GDP | 1.848 | 0.228 | Nom GDP | 1.539 | 0.303 | Nom GDP | 2.083 | 1.324 |
| M1 | 0.831 | 0.728 | M3 | 0.925 | 0.932 | Bank lend. | 0.160 | 3.427* | Bill Rate | 0.885 | 0.461 |
| Nom GDP | Broad money | Nom GDP | AFI lend. | Nom GDP | Credit | ||||||
| Nom GDP | 1.458 | 0.284 | Nom GDP | 1.536 | 1.523 | GDP | 1.424 | 0.592 | |||
| Broad money | 2.600 | 0.747 | AFI lend. | 2.338 | 3.791* | Credit | 2.866* | 4.885** | |||
| 1969:2–1988:3 | |||||||||||
| Real GDP | M1 | Real GDP | M3 | Real GDP | Bank lend. | Real GDP | Bill Rate | ||||
| Real GDP | 2.764* | 0.826 | Real GDP | 2.415 | 1.518 | Real GDP | 2.389 | 0.760 | Real GDP | 2.175 | 0.312 |
| M1 | 1.103 | 3.592* | M3 | 0.489 | 4.749** | Bank lend. | 1.202 | 9.844** | Bill Rate | 1.290 | 0.065 |
| 1978:1–1988:3 | |||||||||||
| Real GDP | M1 | Real GDP | M3 | Real GDP | Bank lend. | Real GDP | Bill Rate | ||||
| Real GDP | 1.882 | 1.075 | Real GDP | 1.535 | 0.853 | Real GDP | 1.410 | 1.324 | Real GDP | 1.569 | 1.171 |
| M1 | 0.941 | 0.702 | M3 | 1.227 | 0.608 | Bank lend. | 0.658 | 2.759* | Bill Rate | 0.822 | 0.652 |
| Real GDP | Broad money | Real GDP | AFI lend. | Real GDP | Credit | ||||||
| Real GDP | 1.430 | 0.982 | Real GDP | 1.115 | 1.273 | Real GDP | 1.069 | 1.252 | |||
| Broad money | 2.652 | 0.682 | AFI lend. | 5.507** | 2.688* | Credit | 4.754** | 3.265* | |||
| 1. Calculated values for F-tests of the hypothesis that the coefficients on lags of explanatory variables are jointly zero. An * denotes significance at the 5 per cent level, ** at the 1 per cent level. | |||||||||||
| 1969:2–1988:3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nom GDP | Bill rate | M1 | Nom GDP | Bill rate | M3 | Nom GDP | Bill rate | Bank lend. | |||
| Nom GDP | 2.209 | 1.266 | 1.341 | Nom GDP | 2.016 | 0.751 | 1.120 | Nom GDP | 1.209 | 1.477 | 1.846 |
| Bill Rate | 0.238 | 1.430 | 3.902** | Bill rate | 0.402 | 0.602 | 2.718* | Bill rate | 0.530 | 0.215 | 0.919 |
| M1 | 0.605 | 6.842** | 1.489 | M3 | 0.958 | 4.344** | 4.031** | Bank lend. | 0.656 | 2.544* | 9.460** |
| 1978:1–1988:3 | |||||||||||
| Nom GDP | Bill rate | M1 | Nom GDP | Bill rate | M3 | Nom GDP | Bill rate | Bank lend. | |||
| Nom GDP | 3.475* | 0.370 | 2.616 | Nom GDP | 1.576 | 1.117 | 0.167 | Nom GDP | 1.762 | 1.598 | 0.658 |
| Bill Rate | 0.396 | 1.418 | 1.692 | Bill rate | 0.289 | 0.694 | 1.584 | Bill rate | 0.876 | 0.391 | 0.518 |
| M1 | 0.448 | 3.470* | 1.215 | M3 | 0.810 | 0.293 | 0.884 | Bank lend. | 0.172 | 0.039 | 2.707 |
| Nom GDP | Bill rate | Broad money | Nom GDP | Bill rate | AFI lend. | Nom GDP | Bill rate | Credit | |||
| Nom GDP | 1.678 | 1.170 | 0.262 | Nom GDP | 2.149 | 1.989 | 2.181 | Nom GDP | 1.421 | 2.518 | 1.770 |
| Bill Rate | 0.579 | 1.648 | 4.563** | Bill rate | 1.194 | 0.285 | 1.756 | Bill rate | 1.163 | 0.396 | 0.959 |
| Broad money | 2.839* | 1.830 | 1.017 | AFI lend. | 1.197 | 0.482 | 2.085 | Credit | 3.690 | 1.000 | 5.744** |
| 1969:2–1988:3 | |||||||||||
| Real GDP | Bill rate | M1 | Real GDP | Bill rate | M3 | Real GDP | Bill rate | Bank lend. | |||
| Real GDP | 2.375 | 0.159 | 0.639 | Real GDP | 1.934 | 0.705 | 1.868 | Real GDP | 2.152 | 0.344 | 0.767 |
| Bill Rate | 0.511 | 1.269 | 3.606* | Bill rate | 1.017 | 0.667 | 2.815* | Bill rate | 1.481 | 0.267 | 1.336 |
| M1 | 0.663 | 7.617** | 1.954 | M3 | 0.341 | 4.604** | 5.689** | Bank lend. | 1.514 | 2.962* | 13.437** |
| 1978:1–1988:3 | |||||||||||
| Real GDP | Bill rate | M1 | Real GDP | Bill rate | M3 | Real GDP | Bill rate | Bank lend. | |||
| Real GDP | 1.662 | 0.901 | 0.819 | Real GDP | 1.528 | 1.270 | 0.984 | Real GDP | 1.347 | 0.880 | 1.011 |
| Bill Rate | 0.377 | 1.584 | 1.732 | Bill rate | 0.274 | 0.859 | 1.627 | Bill rate | 0.769 | 0.627 | 0.468 |
| M1 | 0.640 | 3.609 | 0.886 | M3 | 1.174 | 0.384 | 0.524 | Bank lend. | 0.611 | 0.041 | 2.224 |
| Real GDP | Bill rate | Broad money | Real GDP | Bill rate | AFI lend. | Real GDP | Bill rate | Credit | |||
| Real GDP | 1.813 | 1.146 | 0.979 | Real GDP | 1.281 | 0.921 | 1.009 | Real GDP | 0.990 | 2.018 | 2.098 |
| Bill Rate | 0.275 | 1.832 | 4.174** | Bill rate | 0.868 | 0.171 | 1.467 | Bill rate | 0.613 | 0.431 | 0.475 |
| Broad money | 2.438 | 1.430 | 0.754 | AFI lend. | 3.727* | 0.505 | 0.949 | Credit | 5.359** | 0.882 | 3.616* |
| 1. Calculated values for F-tests of the hypothesis that the coefficients on lags of explanatory variables are jointly zero. An * denotes significance at the 5 per cent level, ** at the 1 per cent level. | |||||||||||
Tables B3 and B4 show results using PFD as the activity variable. The main difference with earlier results here is that PFD leads broader aggregates more often, and that the narrow monetary aggregates M1 and M3 lead PFD when the 1970s data are included in the sample period.
| 1969:2–1988:3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nom PFD | M1 | Nom PFD | M3 | Nom PFD | Bank lend. | Nom PFD | Bill Rate | ||||
| Nom PFD | 1.824 | 2.813* | Nom PFD | 1.626 | 2.736* | Nom PFD | 1.420 | 1.004 | Nom PFD | 2.559* | 0.284 |
| M1 | 1.306 | 3.277* | M3 | 0.619 | 4.757** | Bank lend. | 1.581 | 8.256** | Bill Rate | 0.944 | 0.197 |
| 1978:1–1988:3 | |||||||||||
| Nom PFD | M1 | Nom PFD | M3 | Nom PFD | Bank lend. | Nom PFD | Bill Rate | ||||
| Nom PFD | 0.061 | 1.490 | Nom PFD | 0.701 | 2.926 | Nom PFD | 0.273 | 1.153 | Nom PFD | 0.189 | 0.062 |
| M1 | 2.516 | 1.720 | M3 | 0.101 | 0.800 | Bank lend. | 0.281 | 3.322* | Bill Rate | 2.387 | 0.578 |
| Nom PFD | Broad Money | Nom PFD | AFI lend. | Nom PFD | Credit | ||||||
| Nom PFD | 0.157 | 1.289 | Nom PFD | 0.180 | 0.383 | Nom.PFD | 0.235 | 0.332 | |||
| Broad money | 3.209* | 1.546 | AFI lend. | 1.738 | 1.875 | Credit | 0.606 | 3.329* | |||
| 1969:2–1988:3 | |||||||||||
| Real PFD | M1 | Real PFD | M3 | Real PFD | Bank lend. | Real PFD | Bill Rate | ||||
| Real PFD | 0.192 | 3.186* | Real PFD | 0.643 | 3.971** | Real PFD | 0.222 | 1.704 | Real PFD | 0.555 | 1.571 |
| M1 | 1.438 | 3.160* | M3 | 0.716 | 5.112** | Bank lend. | 0.904 | 9.071** | Bill Rate | 4.501** | 0.934 |
| 1978:1–1988:3 | |||||||||||
| Real PFD | M1 | Real PFD | M3 | Real PFD | Bank lend | Real PFD | Bill Rate | ||||
| Real PFD | 0.232 | 1.978 | Real PFD | 0.613 | 2.301 | Real PFD | 0.296 | 1.093 | Real PFD | 0.320 | 0.280 |
| M1 | 1.762 | 1.512 | M3 | 0.371 | 0.876 | Bank lend. | 0.767 | 3.091* | Bill Rate | 3.325* | 0.977 |
| Real PFD | Broad money | Real PFD | AFI lend. | Real PFD | Credit | ||||||
| Real PFD | 0.365 | 2.388 | Real PFD | 0.356 | 1.393 | Real PFD | 0.369 | 0.898 | |||
| Broad money | 3.984* | 1.519 | AFI lend. | 4.607** | 1.009 | Credit | 2.169 | 2.046 | |||
| 1. Calculated values for F-tests of the hypothesis that the coefficients on lags of explanatory variables are jointly zero. An * denotes significance at the 5 per cent level, ** at the 1 per cent level. | |||||||||||
| 1969:2–1988:3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nom PFD | Bill rate | M1 | Nom PFD | Bill rate | M3 | Nom PFD | Bill rate | Bank lend. | |||
| Nom PFD | 1.409 | 0.180 | 2.543* | Nom PFD | 1.408 | 0.126 | 2.409 | Nom PFD | 1.734 | 0.811 | 1.511 |
| Bill Rate | 0.180 | 1.504 | 3.581* | Bill rate | 0.274 | 0.634 | 2.338 | Bill rate | 0.679 | 0.271 | 0.859 |
| M1 | 1.336 | 8.305** | 1.843 | M3 | 0.741 | 4.953** | 5.007** | Bank lend.. | 1.753 | 2.828* | 11.307** |
| 1978:1–1988:3 | |||||||||||
| Nom PFD | Bill rate | M1 | Nom PFD | Bill rate | M3 | Nom PFD | Bill rate | Bank lend. | |||
| Nom PFD | 0.293 | 0.837 | 2.224 | Nom PFD | 0.403 | 0.290 | 2.871* | Nom PFD | 0.342 | 0.272 | 1.253 |
| Bill Rate | 0.785 | 0.629 | 0.832 | Bill rate | 1.315 | 0.691 | 1.383 | Bill rate | 2.664 | 0.840 | 0.892 |
| M1 | 0.798 | 2.207 | 1.270 | M3 | 0.138 | 0.341 | 0.579 | Bank lend. | 0.307 | 0.067 | 2.749* |
| Nom PFD | Bill rate | Broad money | Nom PFD | Bill rate | AFI lend. | Nom PFD | Bill rate | Credit | |||
| Nom PFD | 0.079 | 0.182 | 1.271 | Nom PFD | 0.185 | 0.065 | 0.345 | Nom PFD | 0.244 | 0.086 | 0.322 |
| Bill Rate | 1.069 | 1.670 | 3.531* | Bill rate | 1.948 | 0.287 | 1.183 | Bill rate | 1.884 | 0.568 | 0.414 |
| Broad money | 2.077 | 0.709 | 1.337 | AFI lend. | 0.961 | 0.711 | 1.806 | Credit | 1.065 | 0.620 | 3.706* |
| 1969:2–1988:3 | |||||||||||
| Real PFD | Bill rate | M1 | Real PFD | Bill rate | M3 | Real PFD | Bill rate | Bank lend. | |||
| Real PFD | 0.236 | 0.671 | 2.116 | Real PFD | 0.564 | 0.953 | 3.139* | Real PFD | 0.473 | 1.256 | 1.380 |
| Bill Rate | 1.631 | 1.695 | 1.816 | Bill rate | 3.391* | 1.485 | 2.244 | Bill rate | 4.667** | 1.414 | 1.437 |
| M1 | 0.778 | 7.346** | 1.927 | M3 | 0.872 | 5.003** | 6.232** | Bank lend. | 1.620 | 3.395* | 12.866** |
| 1978:1–1988:3 | |||||||||||
| Real PFD | Bill rate | M1 | Real PFD | Bill rate | M3 | Real PFD | Bill rate | Bank lend. | |||
| Real PFD | 0.110 | 0.208 | 1.679 | Real PFD | 0.581 | 0.452 | 2.265 | Real PFD | 0.500 | 0.447 | 1.175 |
| Bill Rate | 1.554 | 0.737 | 0.899 | Bill rate | 1.833 | 1.015 | 1.172 | Bill rate | 3.153* | 1.110 | 0.608 |
| M1 | 0.684 | 2.773 | 1.315 | M3 | 0.543 | 0.508 | 0.607 | Bank lend. | 0.953 | 0.266 | 2.881* |
| Real PFD | Bill rate | Broad money | Real PFD | Bill rate | AFI lend. | Real PFD | Bill rate | Credit | |||
| Real PFD | 0.211 | 0.352 | 2.216 | Real PFD | 0.347 | 0.101 | 1.051 | Real PFD | 0.334 | 0.131 | 0.660 |
| Bill Rate | 1.235 | 1.889 | 2.859* | Bill rate | 2.087 | 0.441 | 0.627 | Bill rate | 2.259 | 0.585 | 0.092 |
| Broad money | 2.892* | 0.860 | 1.485 | AFI lend. | 3.714* | 1.024 | 0.664 | Credit | 2.972* | 0.974 | 2.420 |
| 1. Calculated values for F-tests of the hypothesis that the coefficients on lags of explanatory variables are jointly zero. An * denotes significance at the 5 per cent level, ** at the 1 per cent level. | |||||||||||
Table B5 shows the results from Section 5 of the paper when M7PFD is excluded. The main differences are that in the absence of M7PFD, the price differential term PDIFF helps to explain both real GDP and the bill rate, and that the TWI is no longer significant in the equations for exports and imports.
| 1972:2–1988:2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Real GDP | Bill rate | M1 | TWI | PDIFF | Real GDP | Bill rate | M3 | TWI | PDIFF | ||
| Real GDP | 2.019 | 0.821 | 1.824 | 0.759 | 2.653* | Real GDP | 1.316 | 1.182 | 0.466 | 0.714 | 2.835* |
| Bill rate | 0:122 | 6.974** | 4.803** | 0.888 | 3.119* | Bill rate | 0.817 | 7.074** | 5.943** | 1.952 | 4.135** |
| M1 | 1.646 | 2.390 | 1.597 | 1.543 | 0.905 | M3 | 1.543 | 3.258* | 4.604** | 1.378 | 1.833 |
| TWI | 1.383 | 1.150 | 1.364 | 1.157 | 0.672 | TWI | 1.335 | 2.217 | 1.338 | 1.952 | 1.255 |
| PDIFF | 0.509 | 3.368* | 0.269 | 0.777 | 1.262 | PDIFF | 0.352 | 1.356 | 1.866 | 0.400 | 1.126 |
| 1972:2–1988:2 | |||||||||||
| Real Xpts | Bill rate | M1 | TWI | PDIFF | Real Xpts | Bill rate | M3 | TWI | PDIFF | ||
| Real Xpts | 0.692 | 0.482 | 1.956 | 3.048* | 0.523 | Real Xpts | 1.562 | 0.642 | 0.456 | 2.068 | 0.634 |
| Bill rate | 2.068 | 6.833** | 7.658** | 1.311 | 3.134* | Bill rate | 1.822 | 6.965** | 7.474** | 2.119 | 4.849** |
| M1 | 1.764 | 1.294 | 1.750 | 2.527 | 0.855 | M3 | 0.939 | 1.907 | 5.692** | 1.463 | 1.641 |
| TWI | 1.810 | 1.631 | 1.649 | 0.594 | 0.726 | TWI | 1.422 | 2.262 | 1.288 | 1.158 | 1.415 |
| PDIFF | 1.278 | 3.455* | 0.720 | 1.315 | 1.170 | PDIFF | 1.009 | 1.316 | 2.267 | 0.621 | 1.251 |
| 1972:2–1988:2 | |||||||||||
| Real Mpts | Real PFD | M1 | TWI | PDIFF | Real Mpts | Real PFD | M3 | TWI | PDIFF | ||
| Real Mpts | 0.454 | 1.720 | 2.600* | 2.367 | 1.431 | Real Mpts | 0.534 | 2.841* | 2.759* | 2.271 | 1.535 |
| Real PFD | 0.205 | 0.821 | 1.122 | 0.517 | 0.960 | Real PFD | 0.297 | 0.867 | 1.565 | 1.282 | 1.652 |
| M1 | 1.905 | 3.251* | 3.197* | 2.547 | 2.869* | M3 | 1.722 | 2.560 | 1.620 | 1.105 | 3.984** |
| TWI | 0.199 | 0.328 | 1.503 | 0.489 | 0.271 | TWI | 0.891 | 0.728 | 1.114 | 0.825 | 1.446 |
| PDIFF | 3.075* | 1.827 | 1.809 | 0.386 | 2.084 | PDIFF | 3.790** | 0.999 | 6.671** | 0.329 | 2.619* |
| 1. Calculated values for F-tests of the hypothesis that the coefficients on lags of explanatory variables are jointly zero. An * denotes significance at the 5 per cent level, ** at the 1 per cent level. | |||||||||||
The tests reported in Appendix A suggested that some series may contain deterministic time trends in addition to unit roots. If so, these series should arguably be detrended as well as differenced before use in VAR models.
The series in question are:
- M1, M3, Bank lending, M7PFD – linear time trend;
- Broad money, AFI lending, Credit, TWI – quadratic time trend.
Results for tests using detrended data are available from the editors on request. There are few significant differences. If anything, the evidence for measures of activity leading the broader financial aggregates is marginally stronger when the latter are detrended.
Appendix C: Data
The variables used in Section 4 of the paper are defined as follows:
- M1 is currency in the hands of the public plus current deposits with trading banks;
- M3 is M1 plus other deposits of trading banks and deposits of savings banks (net of government and inter-bank deposits);
- broad money is M3 plus borrowings by non-bank financial corporations other than from banks, net of identifiable double-counting;
- bank lending is lending (including bills discounted) to the private sector by trading and savings banks;
- AFI lending is bank lending plus lending (including bills discounted) to the private sector by non-bank financial corporations;
- credit is AFI lending plus bank bills outstanding other than those held by financial intermediaries (which are already included in AFI lending);
- the bill rate is the yield on 90-day bank-accepted bills of exchange;
- PFD is the sum of private consumption and gross fixed capital expenditure on dwellings, non-dwelling construction and plant and equipment from the national accounts; and
- GDP is gross domestic product from the national accounts.
For these series, data sources and methods are as described in the Appendix to Bullock, Morris and Stevens (1989). The only difference is that for national accounts variables, the September quarter 1988 issue of the Quarterly Estimates of National Income and Expenditure, ABS Cat. No. 5206.0 is the source. The constant-price estimates are in 1984/85 prices, rather than 1979/80 prices as in the earlier paper. Constant-price estimates prior to 1974 were calculated by splicing BMS 1979/80 series to 1984/85-based series.
Additional variables used in analysing the external sector in Section 5 are:
| TWI: | Trade-weighted index of average value of the Australian dollar, quarterly average of figures for last day of the month; Reserve Bank of Australia Bulletin. (Rates prior to June 1970 were constructed using weights based on visible trade for 1971–72, and International Monetary Fund par values of exchange rates, as published in International Financial Statistics Vol. 24. For method of calculation, see “The Trade-Weighted Index of Value of the Australian Dollar”, Reserve Bank of Australia Bulletin, April 1984 pp 696–697). |
| M7PFD: | Private final consumption expenditure plus gross fixed capital formation, seasonally adjusted, at 1980 exchange rates and prices, $US billion; OECD Quarterly National Accounts, No. 3, 1988. |
| M7GDP Deflator: | Ratio of current to 1980 price measures of Gross Domestic Product for OECD Major Seven Economies; OECD Quarterly National Accounts, No. 3, 1988. |
The tests for unit roots and time trends used in the main paper require the availability of levels for all series. This raises the issue of adjustments to financial aggregates to allow for the effects of new banks. The method used in BMS was to adjust the growth rates of the aggregates (the procedure is described in the Appendix to BMS). In the present paper, an artificial series for the levels was created by compounding together the growth rates calculated in the same manner as in BMS.
Footnotes
We are grateful to Warwick McKibbin, Warren Tease and Rob Trevor for helpful discussions and comments on an earlier version of this paper. [*]
BMS conjectured that the interest-sensitivity of M1 meant that the information conveyed by it was likely in fact to be the same information as conveyed by short-term interest rates. In this case, perhaps these two cannot really be viewed as independent indicators. [1]
So-named after C.W.J. Granger, who suggested the techniques (see Granger (1969)). Note that the term “causality” is used in a technical sense here. It is a short-hand way of denoting statistical significance in these tests, which help establish certain stylised facts about the data, but does not necessarily imply causality in the strict sense. [2]
Consider the process:

View MathML
Under the null hypothesis that ρ = 1, (as in the case of one unit root), the
usual formula for the large-sample variance of the least-squares estimator
(1 −ρ2) / T gives a value of zero for the variance
of ρ when the true variance is non-zero. Applying conventional asymptotic
theory to this type of model would clearly give misleading results. Thus
usual least-squares techniques and ‘t’-tests for the value of
ρ are not valid.
[3]
Subsidiary tests were conducted in which the affected series were first detrended by regressing the first-differenced series on a constant and a first or second-order time trend, and the residuals from those regressions were then used in estimation. This change makes little difference to test results, which are available from the editors on request. [4]
It should be noted, of course, that this sort of specification ignores the potential long run relationships between the levels of the time series. Series may be “cointegrated”, that is, they may “trend together”. But it is not the purpose of this paper to pursue that issue. For a discussion of cointegration, see, inter alia, Engle and Granger (1987). [5]
For models with seasonally adjusted data, two lags performed as well as four. But four lags were retained anyway for consistency. [6]
For a discussion of empirical issues in general, see Goodhart (1988); for Australian evidence, see Tease (1988) and Kearney and MacDonald (1988). [7]
A more formal model of an open economy can be found in Genberg (1988). [8]
Statistical tests reported in Appendix A suggest that the trade-weighted index (TWI) and major seven private final demand (M7PFD) series may also have a trend component. Models using detrended variables show results similar to models without detrended variables. Results are available from the editors on request. [9]
Models estimated without M7PFD, however, show a weaker relationship between the TWI and the trade variables. See Appendix B, Table B5. [10]
References
Andersen, L.C. and Jordan, J.L. (1968), “Monetary and Fiscal Actions: A Test of their Relative Importance in Economic Stabilization”, Federal Reserve Bank of St Louis Review, 50, 11, pp 11–24.
Andersen, L.C. and Carlson, K.M. (1970), “A Monetarist Model for Economic Stabilization”, Federal Reserve Bank of St Louis Review, 52, 4, pp 7–27.
Auerbach, R. and Rutner, J. (1978), “A Causality Test of Canadian Money and Income: A Comment on Barth and Bennett”, Canadian Journal of Economics, 11, pp 583–593.
Barth, J.R. and Bennett, J.T. (1974), “The Role of Money in the Canadian Economy: An Empirical Test”, Canadian Journal of Economics, 7, pp 306–311.
Boehm, E.A. (1983), “Cycles in Money, Credit, Wages, Costs, Prices and Business Activity in Australia: A Comparative Study 1948–82”, Melbourne University Department of Economics Research Paper, No. 100.
Bullock, M., Morris, D. and Stevens, G. (1989), “The Relationship Between Financial Indicators and Economic Activity: 1968–1987”, this volume, pp 53–85.
Bullock, M., Stevens, G. and Thorp, S. (1988), “Do Financial Aggregates lead Activity? A Preliminary Analysis”, Reserve Bank of Australia Research Discussion Paper No. 8803, January.
Davis, K. and Lewis, M. (1977), “Money and Income: Evidence from Simple Models”, in Porter, M.G. and Burns, M.E. (eds.), The Australian Monetary System in the 1970s, Monash University, Melbourne.
Dickey, D.A. and Fuller, W.A. (1979), “Distribution of the Estimators for Autoregressive Time Series with a Unit Root”, Journal of the American Statistical Association, 74, pp 427–431.
Dickey, D.A. and Pantula, S.G. (1987), “Determining the Order of Differencing in Autoregressive Processes”, Journal of Business and Economic Statistics, Vol. 5, No. 4, pp 455–461.
Engle, R.F. and Granger, C.W.J. (1987), “Co-integration and Error Correction: Representation, Estimation and Testing”, Econometrica, Vol. 55, No. 2, pp 251–267.
Friedman, M. and Schwartz, A. J. (1982), Monetary Trends in The United States and the United Kingdom: Their Relationship to Income, Prices, and Interest Rates, 1867–1975, University of Chicago Press, Chicago.
Friedman, M. and Schwartz, A.J. (1963), A Monetary History of the United States 1867–1960 , Princeton University Press, Princeton.
Fuller, W. A. (1976), Introduction to Statistical Time Series, Wiley, New York.
Genberg, H. (1988), “The Fiscal Deficit and the Current Account: Twins or Distant Relatives?”, Reserve Bank of Australia Research Discussion Paper No. 8813, December.
Goodhart, C.A.E. (1988), “The Foreign Exchange Market: A Random Walk with a Dragging Anchor”, Economica, Vol. 55, No. 220, pp 437–460.
Granger, C.W.J. (1969), “Investigating Casual Relations by Econometric Models and Cross Spectral Methods”, Econometrica, Vol. 37, No. 3, pp 424–35.
Hendry, D.F. and Ericsson, N.R. (1983), “Assertion Without Empirical Basis: An Econometric Appraisal of Friedman and Schwartz's ‘Monetary Trends in the United Kingdom’” in “Monetary Trends in the United Kingdom”, Bank of England Panel of Academic Consultants Paper No. 22.
Kearney, C. and. MacDonald, R. (1988), “Modelling the Australian-US dollar Exchange Rate during the Recent Float”, University of New South Wales Centre for Applied Economic Research Research Report.
Nelson, C.R. and Plosser, C.I. (1982), “Trends and Random Walks in Macroeconomic Time Series”, Journal of Monetary Economics, 10, pp 139–162.
Sarlo, C. (1979), “The Role of Money in the Canadian Economy: Fixed vs Flexible Exchange Rates”, Canadian Journal of Economics, 12, pp 89–93.
Sharpe, B. and Miller, M. (1975), “The Role of Money in the Canadian Economy”, Canadian Journal of Economics, 8, pp 289–290.
Sharpe, I.G. (1975), “The Money Supply, Financing Government and Economic Activity”, Economic Papers, No. 50, pp 23–43.
Sheppard, W.R. (1973), “Money and Economic Activity in Australia”, Conference Paper prepared for Australia and New Zealand Association for the Advancement of Science 45th Congress, Perth, August.
Sims, C. A. (1972), “Money, Income and Causality”, American Economic Review, 62, pp 540–52.
Sims, C. A. (1980), “Comparison of Interwar and Postwar Business Cycles: Monetarism Reconsidered”, American Economic Review, 70, pp 250–257.
Stock, J.H. and Watson, M.W. (1988), “Testing for Common Trends”, Journal of the American Statistical Association, Vol. 83, No. 404, Theory and Methods, pp 1097–1107.
Suzuki, Y., Kuroda, A. and Shirakawa, H. (1988), “Monetary Control Mechanism in Japan”, Bank of Japan Monetary and Economic Studies, Vol. 6, No. 2, pp 1–27.
Tease, WJ. (1988), “Speculative Efficiency and the Exchange Rate: Some Evidence Since the Float”, Economic Record, Vol. 64, No. 184, pp 2–13.
Williams, D., Goodhart, C.A.E. and Gowland, D.H. (1976), “Money, Income and Causality: The U.K. Experience”, American Economic Review, 66, pp 417–23.
Postscript: Test Results Using Real Financial and Real Activity Variables
1. Introduction
The tests reported in the papers by Bullock, Morris and Stevens (BMS) and Stevens and Thorp (S&T) compared nominal financial variables with both real and nominal measures of activity. It was suggested at the Conference[1] that those tests should be complemented by comparisons between real interest rates and real activity. Well-defined measures of real interest rates would, in principle, be able to account for variations in inflationary expectations which would affect comparisons of nominal interest rates and real activity. This postscript presents some results from tests using real variables.
Real interest rates are defined as nominal rates less the expected rate of inflation over the life of the asset or loan. Alternative assumptions about formulation of expectations imply different real interest rates for any given nominal rate. The tests reported here were conducted using a variety of measures of real interest rates, based on different assumptions about expectations.
For the extensions to the BMS results, the real short-term interest rate is defined as the quarterly bill rate less actual growth in the implicit price deflator for final private spending in the same quarter. A proxy for the steepness or degree of inversity of the yield curve (in this case, the 10-year bond rate less the 90-day bank bill rate) is also used.
Extensions to S&T use two alternative assumptions about the formulation of inflationary expectations. The first is perfect foresight: next period's inflation is correctly anticipated; the second is that current inflationary expectations are formed optimally from an information set containing only past values of prices. The bill rate is deflated using predicted values of inflation from each of these approaches, and included in VAR models in place of the nominal short-term interest rate. Estimates using the yield-curve proxy are also reported.
Section 2 reports graphs and correlation coefficients in the style of BMS, and Section 3 covers extensions to the S&T results.
2. Graphical Relationship and Correlation Results
Figure 1 shows growth in real private final demand, the real 90-day bill rate and the “yield curve”, as measured by the long-short spread, which has been graphed negatively for ease of comparison. A positive value for the yield curve series here implies that short rates exceed long rates – that the yield curve is “inverse” – whereas the reverse is true in the econometric analysis.
There is a reasonable inverse relationship between the real bill rate and spending during the 1980s, a result similar to that found using nominal rates in BMS. In particular, large rises in real interest rates are followed by noticeable downturns in spending. During the 1970s the relationship is not as apparent, because of the long period of negative real rates, but the 1974 downturn in spending was still associated with a sharp tightening in financial conditions.
The yield curve measure is less affected by the inflationary acceleration in the 1970s, and so is more useful for that period. In the 1980s, the two measures provide very similar information. Perhaps the major difference is that the yield curve measure suggests that financial conditions were nowhere near as tight in 1982 or 1985–86 as in 1974, whereas the real bill rate suggests that they were.
Table 1 shows correlation coefficients between both the measure of real interest rates and the long-short spread, and the growth of real private demand. As in BMS, the interest rate measures are allowed to lead.
| Lead in Quarters | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | ||||||
| 1968–1987 | |||||||||||
| Real bill rate | −.061 | −.143 | −.155 | −.114 | −.149 | −.109 | |||||
| Long-short spread | .309** | .333** | .309** | .114 | .113 | .022 | |||||
| 1968–1980 | |||||||||||
| Real bill rate | .067 | −.028 | −.001 | .133 | .066 | .083 | |||||
| Long-short spread | .297** | .265* | .232 | −.082 | −.021 | −.087 | |||||
| 1980–1987 | |||||||||||
| Real bill rate | .057 | −.263 | −.368** | −.454** | −.472** | −.211 | |||||
| Long-short spread | .307 | .423** | .407** | .396** | .326* | .172 | |||||
| 1983–1987 | |||||||||||
| Real bill rate | −.219 | −.519** | −.434* | −.488** | −.536** | −.428* | |||||
| Long-short spread | .700** | .746** | .550** | .427* | .290 | .038 | |||||
| 1. An asterisk denotes statistical significance at the 10 per cent level; two indicate significance at the 5 per cent level. | |||||||||||
For the full data sample (1968–1987), there are no significant correlation coefficients between the real bill rate and real private demand. The coincident and first two leading correlations for the long-short spread are significant and of the expected (positive) sign.
In the sub-period 1968–80, there are no significant correlations for the real bill rate and the results for the long-short spread are a little weaker than they are over the full sample period.
The bulk of the significant correlations are found over the 1980s. Correlations for real interest rates are a little smaller than those reported using nominal rates in BMS, but overall, the results are not very different. This is not surprising, since the correlation between nominal and real interest rates over this period was 0.9. The inflation rate in the 1980s has been much more stable than in the 1970s, so movements in real and nominal rates have been quite similar. The long-short spread has a leading relationship with real PFD in this period. As in BMS, the correlations are strongest in the post-1983 part of the sample.
3. Extension of S&T Results
(a) Data and Method
The basic data set used for these tests is the set of seasonally adjusted series used in S&T. Money and credit aggregates (and interest rates) are deflated either with the GDP or PFD deflators, depending on which activity variable appears in the model in question.
Consistent with the practice in S&T, all real variables were tested for unit roots and trend components, and transformed accordingly, before the VAR models were estimated. As a result of this, all variables apart from the yield curve proxy were first-differenced. (There was no evidence of stochastic or deterministic trends in the yield curve measure, so it enters the models in levels.) Some tests indicated the presence of first or second-order time-trends as well as a unit root for specific variables, but the models reported here use data that are differenced only, consistent with the method of S&T.[2]
Two proxies for the real interest rate are used in estimation and testing. The “perfect foresight” measure assumed that the expected rate of growth of prices (the GDP or PFD deflator) is equal to next quarter's actual growth in prices, as measured by the log-change in the deflator. The real interest rate is thus calculated as the quarterly 90-day bank bill rate less next period's rate of growth in prices. This procedure means that one quarter's observation must drop off the end of the data set, so all the models are estimated to 1988:2 rather than 1988:3.[3]
Inflationary expectations are also proxied using the within-sample predictions of single-equation OLS models of inflation, incorporating twelve lags of prices and a constant, estimated over the full sample set. Expectations proxied in this manner are labelled “unbiased” expectations.
In addition, the yield curve proxy is used in one set of models instead of the real short-term interest rate.
(b) Results
Tables 2 to 4 show results of “Granger-causality” tests for trivariate VAR models using four lags of each variable and a constant. Each model includes one interest rate variable, one real money or credit aggregate and either real PFD or real GDP. The results should be interpreted in the same way as for the tables in S&T. Significant F-statistics are indicated by one (5 per cent) or two (1 per cent) asterisks.
| 1969:2–1988:2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GDP | Bill rate | M1 | GDP | Bill rate | M3 | GDP | Bill rate | Bank lend. | |||
| GDP | 2.577 | 0.810 | 1.907 | GDP | 2.225 | 1.025 | 1.466 | GDP | 1.742 | 0.947 | 0.915 |
| Bill rate | 0.108 | 5.083** | 5.078** | Bill rate | 0.348 | 3.396* | 3.242* | Bill rate | 0.499 | 2.176 | 1.358 |
| M1 | 0.366 | 13.167** | 1.014 | M3 | 0.566 | 13.432** | 1.755 | Bank lend. | 0.739 | 5.517** | 3.395* |
| 1978:1–1988:2 | |||||||||||
| GDP | Bill rate | M1 | GDP | Bill rate | M3 | GDP | Bill rate | Bank lend. | |||
| GDP | 2.754* | 0.589 | 2.294 | GDP | 1.661 | 0.964 | 0.931 | GDP | 1.634 | 1.581 | 1.440 |
| Bill rate | 0.693 | 5.006** | 1.768 | Bill rate | 1.080 | 3.105* | 0.269 | Bill rate | 1.526 | 3.350* | 0.701 |
| M1 | 1.141 | 2.428 | 0.465 | M3 | 0.275 | 0.718 | 0.570 | Bank lend. | 0.737 | 0.807 | 3.171* |
| GDP | Bill rate | Broad money | GDP | Bill rate | AFI lend. | GDP | Bill rate | Credit | |||
| GDP | 1.961 | 2.094 | 1.827 | GDP | 1.441 | 1.955 | 1.269 | GDP | 1.679 | 1.835 | 1.250 |
| Bill rate | 1.195 | 3.073* | 0.841 | Bill rate | 1.354 | 3.062* | 0.563 | Bill rate | 0.944 | 3.199* | 0.886 |
| Broad money | 0.908 | 1.646 | 0.655 | AFI lend | 2.192 | 0.577 | 1.375 | Credit | 3.639 | 0.955 | 2.384 |
| 1969:2–1988:2 | |||||||||||
| PFD | Bill rate | M1 | PFD | Bill rate | M3 | PFD | Bill rate | Bank lend. | |||
| PFD | 1.539 | 0.762 | 1.808 | PFD | 1.891 | 0.908 | 0.160 | PFD | 1.900 | 1.048 | 0.129 |
| Bill rate | 1.152 | 6.026** | 3.059* | Bill rate | 2.286 | 5.566** | 3.862** | Bill rate | 3.837** | 4.289** | 2.378 |
| M1 | 0.810 | 4.712** | 2.162 | M3 | 0.985 | 4.979** | 3.498* | Bank lend. | 0.924 | 2.812* | 8.422** |
| 1978:1–1988:2 | |||||||||||
| PFD | Bill rate | M1 | PFD | Bill rate | M3 | PFD | Bill rate | Bank lend. | |||
| PFD | 0.841 | 0.210 | 1.419 | PFD | 0.976 | 0.184 | 0.218 | PFD | 1.919 | 0.093 | 0.790 |
| Bill rate | 0.619 | 4.492** | 0.889 | Bill rate | 1.358 | 3.508* | 0.664 | Bill rate | 2.649 | 3.825* | 0.434 |
| M1 | 2.137 | 1.186 | 1.128 | M3 | 0.292 | 0.860 | 1.157 | Bank lend. | 0.302 | 0.855 | 4.635** |
| PFD | Bill rate | Broad money | PFD | Bill rate | AFI lend. | PFD | Bill rate | Credit | |||
| PFD | 0.877 | 0.384 | 1.357 | PFD | 1.867 | 0.123 | 1.235 | PFD | 2.076 | 0.102 | 1.351 |
| Bill rate | 1.005 | 4.729** | 2.032 | Bill rate | 2.450 | 3.710* | 0.345 | Bill rate | 2.558 | 3.822* | 0.551 |
| Broad money | 0.454 | 1.077 | 0.464 | AFI lend. | 1.044 | 0.809 | 1.717 | Credit | 1.112 | 0.968 | 4.269** |
| 1. Calcualted values for F-tests of the hypothesis that the coefficients on lags of explanatory variables are jointly zero. An * denotes significance at the 5 per cent level, ** at the 1 per cent level. | |||||||||||
| 1969:2–1988:2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GDP | Bill rate | M1 | GDP | Bill rate | M3 | GDP | Bill rate | Bank lend. | |||
| GDP | 2.554* | 0.904 | 1.974 | GDP | 2.217 | 1.037 | 1.447 | GDP | 1.729 | 0.932 | 0.870 |
| Bill rate | 0.117 | 5.185** | 5.141** | Bill rate | 0.353 | 3.472* | 3.267* | Bill rate | 0.496 | 2.237 | 1.367 |
| M1 | 0.366 | 13.817** | 1.060 | M3 | 0.598 | 14.612** | 2.019 | Bank lend. | 0.782 | 6.051** | 3.552* |
| 1978:1–1988:2 | |||||||||||
| GDP | Bill rate | M1 | GDP | Bill rate | M3 | GDP | Bill rate | Bank lend. | |||
| GDP | 2.783* | 0.606 | 2.364 | GDP | 1.676 | 0.937 | 0.946 | GDP | 1.635 | 1.546 | 1.450 |
| Bill rate | 0.630 | 4.719** | 1.837 | Bill rate | 0.979 | 2.817* | 0.295 | Bill rate | 1.414 | 3.136* | 0.772 |
| M1 | 1.127 | 2.555 | 0.453 | M3 | 0.253 | 0.879 | 0.578 | Bank lend. | 0.754 | 0.937 | 3.161* |
| GDP | Bill rate | Broad money | GDP | Bill rate | AFI lend. | GDP | Bill rate | Credit | |||
| GDP | 1.958 | 2.056 | 1.837 | GDP | 1.466 | 1.889 | 1.251 | GDP | 1.715 | 1.763 | 1.225 |
| Bill rate | 1.108 | 2.778* | 0.849 | Bill rate | 1.265 | 2.865* | 0.666 | Bill rate | 0.860 | 3.023* | 1.026 |
| Broad money | 0.957 | 1.871 | 0.508 | AFI lend. | 2.201 | 0.669 | 1.280 | Credit | 3.645* | 1.008 | 2.334 |
| 1969:2–1988:2 | |||||||||||
| PFD | Bill rate | M1 | PFD | Bill rate | M3 | PFD | Bill rate | Bank lend. | |||
| PFD | 1.561 | 0.803 | 1.833 | PFD | 1.919 | 0.927 | 0.162 | PFD | 1.943 | 1.068 | 0.132 |
| Bill rate | 1.153 | 6.070** | 3.080* | Bill rate | 2.282 | 5.614** | 3.913** | Bill rate | 3.857** | 4.328** | 2.398 |
| M1 | 0.817 | 4.842** | 2.222 | M3 | 0.975 | 5.817** | 3.582* | Bank lend. | 0.938 | 2.958* | 8.570** |
| 1978:1–1988:2 | |||||||||||
| PFD | Bill rate | M1 | PFD | Bill rate | M3 | PFD | Bill rate | Bank lend. | |||
| PFD | 0.841 | 0.209 | 1.413 | PFD | 0.983 | 0.192 | 0.221 | PFD | 1.935 | 0.100 | 0.792 |
| Bill rate | 0.624 | 4.459** | 0.878 | Bill rate | 1.364 | 3.483* | 0.659 | Bill rate | 2.660 | 3.809* | 0.438 |
| M1 | 2.135 | 1.848 | 1.126 | M3 | 0.285 | 0.864 | 1.155 | Bank lend. | 0.303 | 0.925 | 4.714** |
| PFD | Bill rate | Broad money | PFD | Bill rate | AFI lend. | PFD | Bill rate | Credit | |||
| PFD | 0.885 | 0.376 | 1.342 | PFD | 1.875 | 0.121 | 1.226 | PFD | 2.082 | 0.102 | 1.346 |
| Bill rate | 1.021 | 4.686** | 2.011 | Bill rate | 2.464 | 3.704* | 0.356 | Bill rate | 2.579 | 3.821* | 0.565 |
| Broad money | 0.458 | 1.083 | 0.466 | AFI lend. | 1.060 | 0.872 | 1.756 | Credit | 1.136 | 1.008 | 4.299** |
| 1. Calculated values for F-tests of the hypothesis that the coefficients on lags of explanatory variables are jointly zero. An * denotes significance at the 5 per cent level, ** at the I per cent level. Yield curve calculated as 10-year bond rate less 90-day bank bill rate. | |||||||||||
| 1969:2–1988:2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GDP | Yield curve | M1 | GDP | Yield curve | M3 | GDP | Yield curve | Bank lend. | |||
| GDP | 2.622* | 0.800 | 1.410 | GDP | 2.278 | 0.857 | 0.946 | GDP | 2.028 | 1.334 | 0.974 |
| Yield curve | 0.233 | 8.889** | 3.473* | Yield curve | 0.279 | 10.739** | 2.778* | Yield curve | 0.212 | 5.543 | 4.202 |
| M1 | 0.486 | 7.557** | 1.377 | M3 | 0.299 | 13.114** | 1.393 | Bank lend. | 0.375 | 7.096** | 4.006** |
| 1978:1–1988:2 | |||||||||||
| GDP | Yield curve | M1 | GDP | Yield curve | M3 | GDP | Yield curve | Bank lend. | |||
| GDP | 3.910* | 1.780 | 3.497* | GDP | 2.094 | 0.936 | 0.719 | GDP | 3.846* | 3.386* | 2.981* |
| Yield curve | 0.408 | 12.485** | 0.700 | Yield curve | 0.604 | 16.635** | 2.379 | Yield curve | 0.278 | 10.992** | 1.915 |
| M1 | 1.202 | 0.771 | 0.858 | M3 | 0.475 | 1.073 | 0.490 | Bank lend. | 0.893 | 1.291 | 4.232** |
| GDP | Yield curve | Broad money | GDP | Yield curve | AFI lend. | GDP | Yield curve | Credit | |||
| GDP | 2.517 | 1.499 | 1.058 | GDP | 3.763* | 5.010** | 3.840* | GDP | 3.720* | 4.861** | 3.826* |
| Yield curve | 0.604 | 12.717** | 3.458* | Yield curve | 0.216 | 7.012** | 5.076** | Yield curve | 0.134 | 8.757** | 5.165** |
| Broad money | 0.665 | 2.337 | 1.266 | AFI lend. | 1.735 | 1.198 | 1.943 | Credit | 3.274* | 1.728 | 3.276* |
| 1969:2–1988:2 | |||||||||||
| PFD | Yield curve | M1 | PFD | Yield curve | M3 | PFD | Yield curve | Bank lend. | |||
| PFD | 1.078 | 1.242 | 1.501 | PFD | 1.028 | 1.532 | 0.110 | PFD | 0.973 | 1.573 | 0.183 |
| Yield curve | 0.643 | 7.957** | 2.449 | Yield curve | 1.073 | 8.945** | 1.798 | Yield curve | 1.147 | 6.434** | 3.778** |
| M1 | 1.873 | 2.134 | 4.071** | M3 | 0.942 | 4.108** | 3.490* | Bank lend. | 0.843 | 3.470* | 9.295** |
| 1978:1–1988:2 | |||||||||||
| PFD | Yield curve | M1 | PFD | Yield curve | M3 | PFD | Yield curve | Bank lend. | |||
| PFD | 0.656 | 0.598 | 1.144 | PFD | 0.844 | 0.948 | 0.329 | PFD | 1.246 | 0.370 | 0.429 |
| Yield curve | 0.883 | 10.113** | 0.102 | Yield curve | 1.293 | 10.378** | 0.856 | Yield curve | 1.711 | 8.199** | 1.308 |
| M1 | 2.455 | 0.597 | 1.436 | M3 | 0.740 | 2.048 | 1.026 | Bank lend. | 0.866 | 1.618 | 5.478** |
| PFD | Yield curve | Broad money | PFD | Yield curve | AFI lend. | PFD | Yield curve | Credit | |||
| PFD | 0.879 | 0.758 | 1.060 | PFD | 1.432 | 0.463 | 0.919 | PFD | 1.438 | 0.371 | 0.957 |
| Yield curve | 0.456 | 10.455** | 1.293 | Yield curve | 0.840 | 5.656** | 3.540* | Yield curve | 1.347 | 5.580** | 3.379* |
| Broad money | 0.808 | 3.314* | 1.455 | AFI lend. | 0.599 | 0.462 | 1.191 | Credit | 0.468 | 0.455 | 4.262** |
| 1. Calcualted values for F-tests of the hypothesis that the coefficients on lags of explanatory variables are jointly zero. An * denotes significance at the 5 per cent level, ** at the 1 per cent level. Yield curve calculated as 10-year bond rate less 90-day bank bill rate. | |||||||||||
(i) Models with “Perfect Foresight” Inflationary Expectations
Table 2 reports the “causality” tests for these models. Overall, the results are quite similar to comparable models with nominal variables reported in S&T. Over the full sample period, there is support for a two-way relationship between the narrower money aggregates and real interest rates, and some indication that the real rate leads bank lending. None of these relationships, or any other “off-diagonal” relationships, are evident over the shorter sample.
(ii) Models with “Unbiased” Inflationary Expectations
Results from Table 3 are remarkably similar to those for Table 2. There are only two differences worth noting: real GDP leads real credit, and real PFD leads the real bill rate in the model with bank lending (again consistent with the results in S&T using nominal rates).[4]
(iii) Models with Yield Curve
Table 4 shows a more distinctive set of results. The full-sample results for real M1 and M3 are fairly consistent with comparable results from Tables 2 and 3, since there is evidence for a coincident link between these aggregates and the interest rate measures. The yield curve leads real GDP in three instances, but nowhere does it lead real PFD.
The picture with the broader aggregates is less clear. Real broad money, AFI lending and credit all appear to lead the yield curve, except in the broad money-PFD model where the yield curve leads real broad money. Inclusion of the yield curve also adds to the power of real credit or real lending in explaining real GDP, though real GDP also explains real credit. This result is not found when real PFD is used.
4. Conclusions
Extensions to BMS suggest that there is a relationship between short-term interest rates measured in real terms and growth in private spending over the 1980s. A proxy for the slope of the yield curve is also useful; it is probably a better indicator for the mid 1970s when inflation was more variable.
The more sophisticated tests give little or no evidence of a lead from real short-term interest rates to activity, a result similar to those in S&T. There is some support, on the other hand, for the hypothesis that the yield curve leads real GDP. The timing of the relationship between activity and real financial aggregates is not as clear when the yield curve is used rather than short-term nominal or real interest rates.
Footnotes
See summary of Conference discussion, this volume, pp 162–169. [1]
Results of tests for stationarity are not reported here, but are available from the editors on request. [2]
Although the extra observation is available in models with the yield curve and the alternative real interest rate, the shorter sample is also used in these cases to allow direct comparisons between different measures. [3]
It is interesting to note that the difference in results between models estimated with these alternative assumptions about expectations is very small. In most cases, there are changes only to the second or third decimal place of the ‘F’ – statistics. [4]