Bulletin – June 2019 Australian Economy Can Structural Change Account for the Low Level of Non-mining Investment?
- Download 566KB

Abstract
No, it cannot. Non-mining firms have invested less over the past decade, relative to their output, than they did over the previous two decades, and this decline in investment intensity has been broad based across firms. This reduced investment could contribute to slower economic growth, if, for example, it is associated with decreased adoption of new technologies. This article looks into potential driving forces behind the decline in the rate of investment, finding that it cannot be explained by shifts in industry structure, or the composition of firms by age or date of formation. The size of the decline is consistent with what would be expected given slower technological progress and lower depreciation rates. But there might be other, more cyclical reasons for the observed slowdown in non-mining investment.
Introduction
The production of goods and services typically relies on the use of both capital (e.g. buildings, machinery & equipment, computer software) and labour inputs. To expand production, firms can either increase their stock of capital, hire additional workers, or find ways to use existing inputs more efficiently. Since firms' investment decisions affect their stock of capital, investment is a key channel through which the economy can grow its productive capacity.
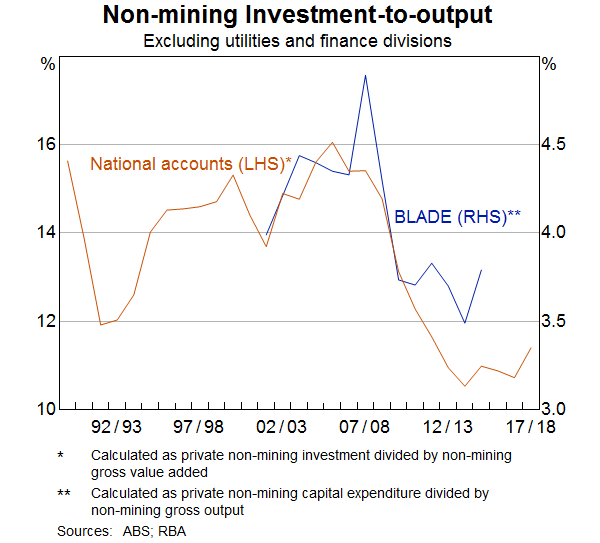
Over the past decade, non-mining firms have tended to invest less intensively than they did in the preceding two decades. In the decade leading up to the Global Financial Crisis (GFC), firms in the non-mining sector invested, on average, between 14 and 16 cents per dollar of output. In the post-GFC period this has declined to between 10 and 12 cents of investment per dollar of output (Graph 1). To put this into context, if non-mining firms invested with a similar intensity today as they did before the GFC, non-mining investment would have been around $54 billion, or one-third, higher in 2017/18 than was actually observed. The slowdown in investment is not unique to Australia; following the GFC, many advanced economies have recorded weaker capital expenditure than expected (CEA, 2017).
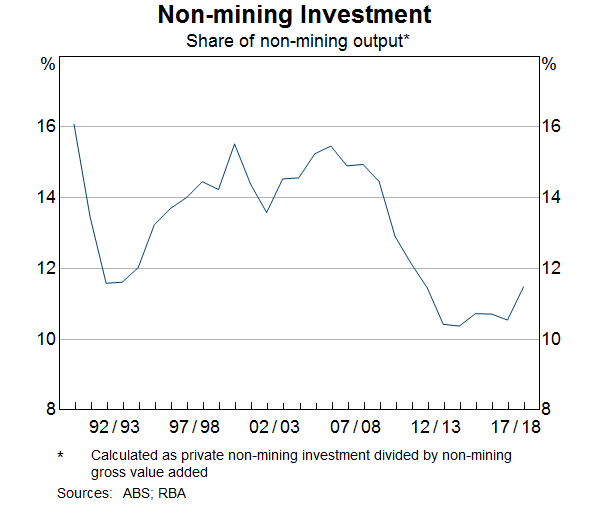
The decline in the economy's investment intensity could have wide-ranging consequences. For example, to the extent that lower investment leads to slower growth in the capital stock, growth in output per worker (also known as labour productivity) is also likely to slow unless there are offsetting technological improvements. All things being equal, this would tend to put downward pressure on wage growth. Moreover, if firms tend to invest in new and more productive capital, a decline in the rate of investment could contribute to a lower rate of technological advancement, and therefore slower economic growth.
Given the possible consequences, we are interested in understanding what has driven the decline in the economy's investment intensity in the past decade. In doing so, we build on past work by van der Merwe et al (2018), which provided an overview of, and evidence regarding, a wide range of potential explanations for the decline in investment intensity. In the first part of this article, we revisit whether changes in industry structure can explain the decline, as well as examining a potential role for changes in the age and cohort composition of firms in the economy. We do this using firm-level tax data from the Business Longitudinal Analysis Data Environment (BLADE), which is ideally suited to such an analysis.[1]
Having demonstrated that compositional change explains only a very small share of the decline in the economy's investment intensity since the GFC, and that the decline is apparent across most firms irrespective of their characteristics, we then consider other explanations. In particular, we present a simple theoretical model of the economy's (long-run) investment intensity. Using this model and aggregate data, we demonstrate that the combination of a slowdown in technological progress and a lower depreciation rate can potentially explain a large share of the decline in the non-mining sector's investment intensity.
Throughout this article, we focus on nominal (rather than real) investment as a share of output. Nominal data are considered more appropriate given difficulties in comparing the level of real investment over time and across industries, particularly due to the large changes in technology over recent decades and the significant shifts in the relative prices of investment goods that have accompanied these changes. However, given real investment has also been relatively subdued in recent years, this focus on nominal data is unlikely to substantially affect our conclusions.
Compositional Change
Industry structure
If economic activity shifts away from investment-intensive sectors, such as manufacturing, to sectors with lower intensities, such as services, then, in principle, this could account for a decline in the overall (non-mining) investment intensity (Adeney, 2018, van der Merwe et al 2018). But although economic activity has shifted in this way over the decades, the shift accounts for only a small part of the more recent decline in investment intensity; most of the decline has occurred within sectors. Previous research showed this for broad sectors such as manufacturing and services, using National Accounts data (van der Merwe et al (2018); Graph 2). We confirm that this finding is also true for more disaggregated industry groupings using firm-level data from BLADE.[2] That is, the decline in investment intensity has not occurred because activity had shifted within sectors to less investment-intensive industries in each sector.
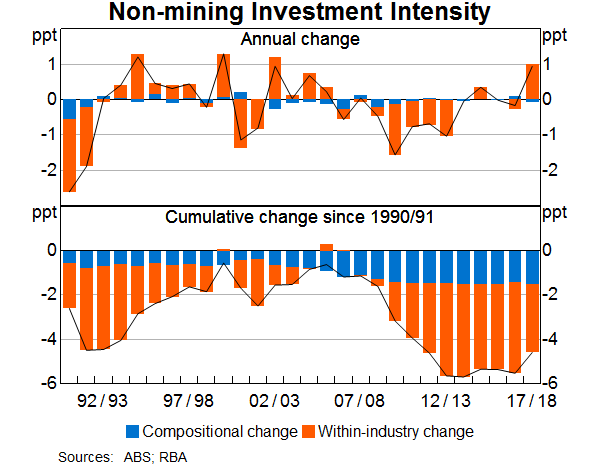
To demonstrate this finding, we show results for four sectors that account for much of the decline in the aggregate investment intensity based on firm-level data. These sectors are: transport, ‘rental, hiring and real estate’ (RHRE), construction and manufacturing. We find that for three of the sectors we examine – transport, RHRE and construction – compositional change has actually contributed positively to investment intensity (Table 1). The manufacturing sector is an exception: around one-third of the decline in its investment intensity is explained by changes in the type of manufacturing done now, compared with the pre-GFC period. In particular, shifts away from ‘traditional’ manufacturing industries such as non-ferrous metal manufacturing, aluminium smelting and motor vehicle manufacturing appear to have played some role.
| Total | Within-industry effect | Compositional effect | |
|---|---|---|---|
| Total Non-mining | −0.99 | −1.21 | 0.22 |
| Transport | −5.50 | −7.30 | 1.80 |
| Rental, hiring & real estate | −5.41 | −6.12 | 0.71 |
| Manufacturing | −0.84 | −0.56 | −0.27 |
| Construction | −1.27 | −1.31 | 0.03 |
|
Sources: ABS; RBA |
|||
Investment intensity over the firm lifecycle
At a high level, there are two potential explanations for the broad-based declines in the investment intensities of industries: either they reflect some sort of compositional shift between firms, such as an increase in the prevalence of older, less investment-intensive firms; or they reflect broad-based declines in the investment intensities of all firms. We consider two potential compositional shifts, both of which are motivated by overseas evidence.
The first is a shift in the age distribution of firms. As we will show, young firms are typically more investment intensive than mature firms. This finding is intuitive, given young firms need to buy machinery, fit out their shop or purchase other capital goods before they can ramp up production. Accordingly, any shift in economic activity away from young firms, and towards older firms, could weigh on the economy's aggregate investment intensity. Other research has noted a trend of declining firm entry rates both in Australia (Productivity Commission, 2015) and overseas (Pugsley, Sahin & Karahan 2015). Lower firm entry rates will mean fewer young firms and, all else being equal, this could potentially contribute to a decline in the economy's investment intensity.
The second compositional shift we consider is a change in the cohort composition of firms. Firms ‘born’ at different points in time could have inherently different investment intensities. For example, firms born during periods of weak economic growth, such as the GFC, may be inherently less investment intensive than firms born during other periods. This would be consistent with evidence from the United States, which shows that firms born during the GFC remained smaller than firms born during other periods (Moreira, 2017). As such, this could contribute to the decline in the economy's investment intensity, if firms from low-intensity cohorts start to make up an increasingly large share of the economy.
To quantify age and cohort effects, we use an age-period-cohort (APC) model with firm-level data from BLADE. APC models are useful in this context because they allow us to separately identify the effects of ageing from the effects of belonging to a particular cohort, or of being observed in a particular time period.[3]
We start by considering age effects. Our results show that firms are most investment intensive in their first year of life and that the sharpest drop-off occurs as they move from their first to second year of existence (Graph 3). Firms' investment intensities continue to decline for a few years, but then flatten out from the age of five onwards.
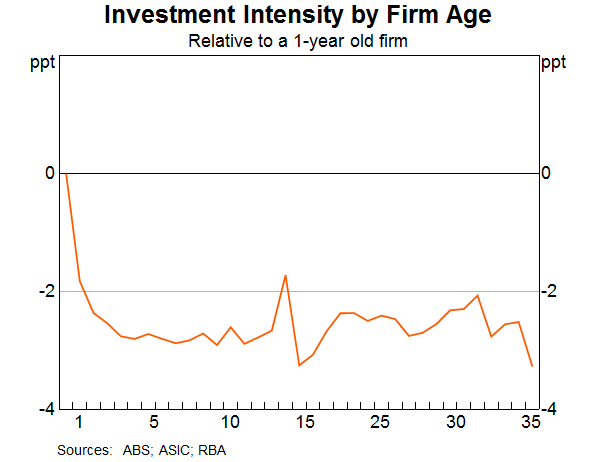
Moreover, the share of output produced by young firms (defined here as between 1 and 5 years of age) has declined by around 4 percentage points relative to the pre-GFC period. At face value, the two observations together would suggest that age effects could be important in explaining the decline in the economy's investment intensity. However, we estimate that the reduction in the share of output accounted for by young firms explains at most 10 per cent of the total decline.[4]
In terms of cohort composition, we want to consider whether firms born or established during periods of low growth, such as in the GFC period, have permanently lower investment intensities. While we do find some weak evidence that firms born during periods of slower economic growth tend to be less investment intensive than other firms, this is not particularly robust to different modelling choices. Further, these ‘cohort’ effects are not economically significant. Firms born during the GFC are estimated to be only slightly less investment intensive than firms established during more normal economic conditions. Further, since firms born during the GFC make up only a very small portion of the economy, their effect on the aggregate non-mining investment intensity is close to zero.
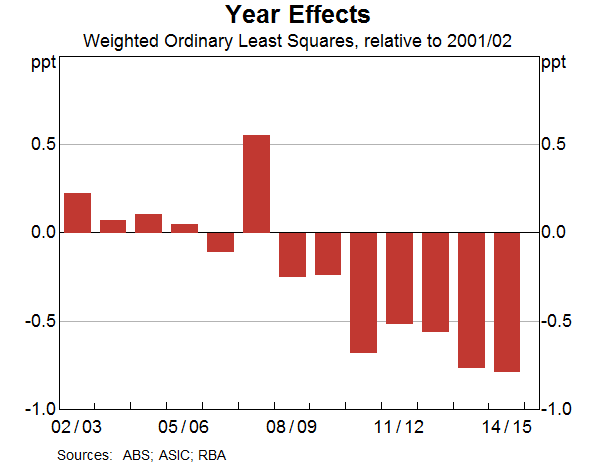
Taken together, our results do not provide evidence of significant compositional effects at the firm level. Rather, they suggest that the decline in the non-mining sector's aggregate investment intensity has been broad based across all firms. To demonstrate this further, we can examine the estimated year effects from the model. Year effects capture the (weighted) average investment intensity across all firms in a given period, after we account for other relevant factors such as their age, cohort and industry. As a result, they can be thought of as capturing any aggregate factors that affect all firms equally at a given period in time.
The estimated year effects have been consistently negative since 2008/09, suggesting that, on average, all firms have tended to be less investment intensive than expected, given factors such as their age and cohort (Graph 4). Moreover, the magnitude of the effects is similar to the overall decline in the aggregate investment intensity in BLADE (see Graph A1). This is consistent with earlier findings that there is little role for compositional change in explaining the decline in the economy's investment intensity.
Long-run Determinants of Non-mining (Market Sector) Investment[5]
Because the decline in firms' investment intensity appears to be broadly based, there may be some economy-wide factors that have been depressing firms' investment intensity. One useful starting place to look for such factors is to examine the theoretical determinants of an economy's investment intensity – those factors that would be expected to determine the economy's investment intensity in the long run. In this section, we focus our analysis on the non-mining market sector, which excludes health, education and public administration. We do this to avoid complications related to measuring productivity growth in the non-market sector. The trends in investment intensity are similar to those in the overall non-mining sector, although the decline has been more pronounced in the non-mining market sector.
As discussed in Jenner et al (2018), using a simple theoretical model, the non-mining economy's long-run investment-to-output ratio should depend on three things: the economy's capital-to-output ratio; the growth rate of output, which in turn will be a function of productivity growth and growth in inputs; and depreciation rates.[6] This reflects the fact that additional investment will be required to both support future economic growth and to replace worn-out capital. Below we consider each of the three factors and how they have changed over time. We note here that this exercise is descriptive in nature and focuses on the long run, and that there may be other factors outside of our stylised model that can help to explain the observed decline in investment intensity.
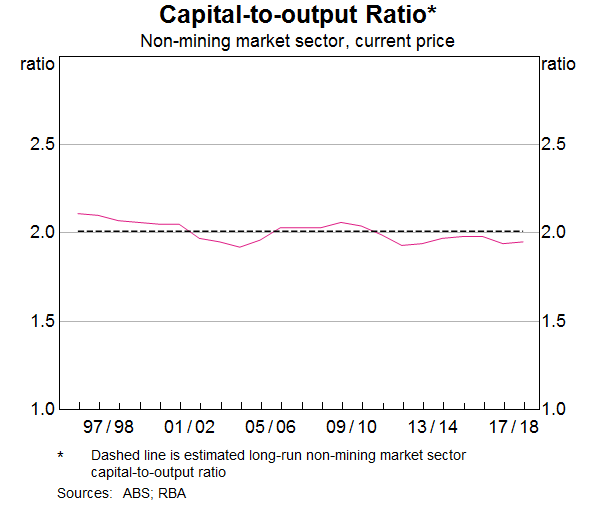
First, we consider the capital-to-output ratio. Economic growth theory suggests that the capital-to-output ratio should be constant over time, which appears to be broadly true in the Australian data, at least over our sample period (Graph 5). This suggests that changes in the ratio cannot explain the decline in the investment-to-output ratio in the past decade. For the rest of the analysis, we assume that the capital-to-output ratio is equal to the average capital-to-output over the sample, which is about 2. A ratio of 2 indicates that, on average, firms require two dollars of capital – such as buildings, motor vehicles or computer hardware – to produce one dollar of output each year.
The growth rate of non-mining output is the second determinant of investment intensity in our model. The growth rate of output is important because changes in production and capital must match each other over time if the capital-to-output ratio is to remain constant. Therefore, the faster (slower) that output expands, the more (less) investment will be required to increase the stock of capital.
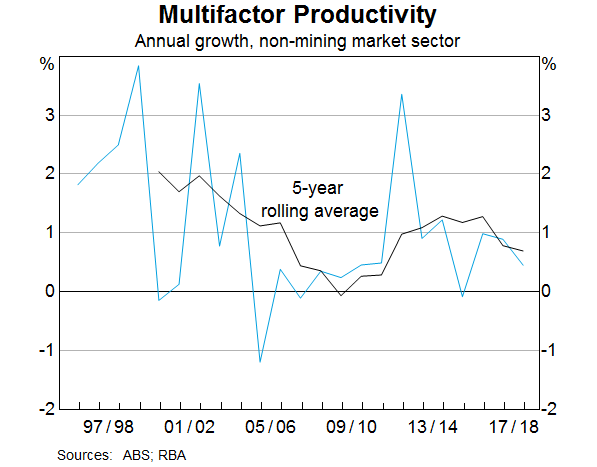
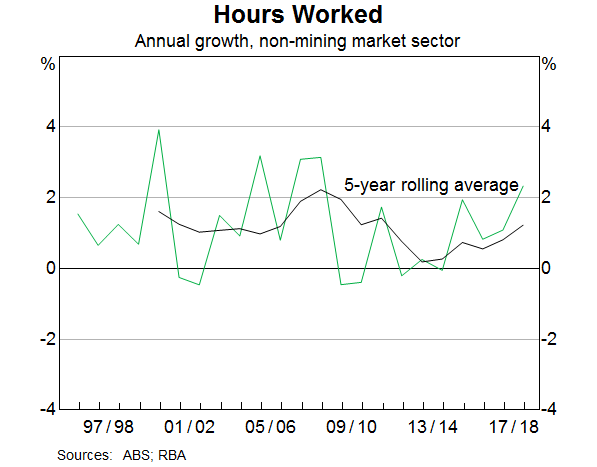
Economic theory suggests that, in the long run, the growth rate of output is determined by growth in productivity and growth in the supply of labour. Graphs 6 and 7 show both determinants, and provide some evidence of lower productivity growth over the past decade, although the precise magnitude of the slowdown is sensitive to the reference period. More generally, a slowdown in productivity growth has been widely documented both in Australian and overseas (D'Arcy and Gustafsson, 2012; McCririck and Rees, 2016), with some overseas research also finding that the decline in productivity growth preceded the GFC (Fernald et al, 2017).
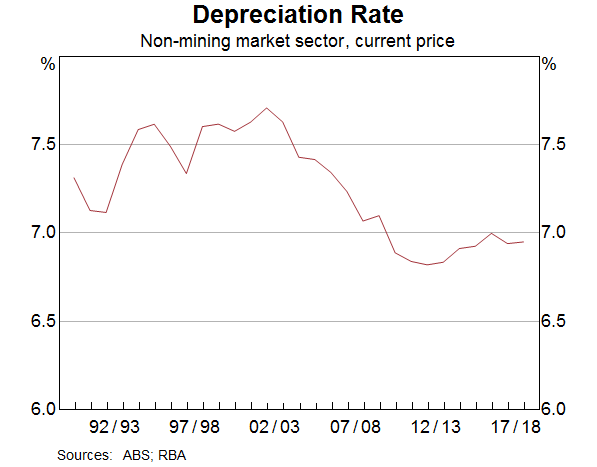
The final component of our calculation is the depreciation rate. The depreciation rate measures the amount of firms' capital that is ‘consumed’ or ‘worn out’ in a given period. In our model, some investment is required simply to offset depreciation and to maintain the value of the existing stock of capital. The ABS measure of the depreciation rate for the non-mining market sector has declined notably since the early 2000s, implying that less investment is required to maintain the existing capital stock than used to be the case (Graph 8). The decline in the depreciation rate largely reflects a compositional shift in the capital stock towards longer lived assets, such as buildings & engineering structures (i.e. office towers, roads and railways), which tend to be replaced less often than other types of capital, such as machinery & equipment.
To quantify the effects of these three factors, we can use them to construct an estimate of the long-run investment intensity of the non-mining market sector that we would expect the economy to eventually reach over time.[7]
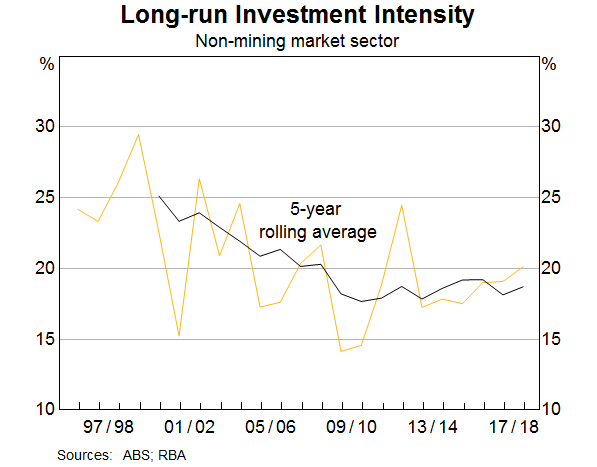
We estimate that the non-mining market sector's long-run investment intensity has decreased by about 5 percentage points over the sample, driven by weaker multifactor productivity growth and a lower depreciation rate (Graph 9). This suggests that declining rates of (long-run) output growth and depreciation could explain most of the recent decline in the economy's investment intensity. Despite this, we can't rule out the possibility that other cyclical factors may have also weighed on investment intensity in recent years. For example, an increase in risk premiums or risk aversion may have also depressed firms' investment over the post-GFC period.
Conclusion
We find that the decrease in the economy's investment intensity has been broad based across most firms and that shifts in the industry, age or cohort composition of firms have not had a material impact. This is consistent with a lower long-run investment intensity for the entire non-mining market sector. We estimate that the economy's long-run investment intensity has declined over the past decade, reflecting weak multifactor productivity growth and a lower depreciation rate.
Appendix A
For our analysis of compositional change, we use longitudinal firm-level data from BLADE.
Our measures of investment and output are both derived from firms' Business Activity Statements (BAS). We define the investment-to-output ratio as firms' capital expenditure divided by their gross output. The sample covers 2001/02 to 2014/15.
For all analysis using BLADE, we exclude firms:
- in the finance and utilities divisions due to conceptual issues with the calculation of gross output, as well as public sector organisations;
- in a handful of industries where the data appears suspect.
For our analysis of firm age and cohort effects, we also exclude firms:
- with an investment-to-output ratio above the 99th percentile (around 160 per cent);
- born prior to 1980 and after 2013 due to the small sample size of firms born outside of this period.
Further, we combine the BAS data with data on the date of firm formation, which we use to calculate firms' ages. One feature of the data, however, is that there is a substantial increase in the coverage of firms born from 2001/02 onwards.[8] This will initially inflate the measured share of output produced by young firms in our sample. Moreover, this bias will tend to decline over time, as additional observations with improved firm coverage become available. The effect of this will be to exaggerate the decline in the share of output produced by young firms from 2001/02 onwards, likely causing us to overstate the effect of an ageing business population.
Appendix B
We want to decompose the decrease in the aggregate investment intensity into:
- A compositional effect that is due to industries with a low investment intensity growing faster than the average division.
- Within-industry effects, which are due to investment intensities within industries decreasing.
Denoting industries as x, first we note that the aggregate investment intensity, ,can be expressed as the sum of the individual industries' ratios, , weighted by their shares of total output, :
The change in the aggregate investment intensity over some period, , is then:
The within-industry effect, , is calculated by assuming that the weights are unchanged across the two periods (at their average level):
The compositional effect, , is calculated similarly, by assuming the industry investment intensities remain unchanged:
Appendix C
To estimate the firm-level effect of age and cohort, we estimate an Age-Period-Cohort (APC) model. In APC models, age effects capture lifecycle patterns, period effects capture aggregate shocks that affect all firms at a given point in time, and birth cohort effects capture differences in investment-intensities across generations. The APC model shows the outcome of interest for firm i at time t as the sum of age, year and cohort dummies, and an error term:
Since there is an exact linear relationship between age, time and cohort (i.e. age = year – cohort), all three components cannot be identified at the same time. We take two different approaches to address this issue:
- Estimate a fixed effects model, which strips out firm-specific time-invariant factors such as their birth cohort.
- Replace the cohort dummy variable with a proxy variable that captures economic conditions in the year the firm was born. Our main proxy variable is real gross national expenditure growth.
For both models, we include an additional control variable for firm size, measured as employment.[9] For the second approach, we also include a number of time-invariant controls, including firm's legal structure (i.e. company or unincorporated), industry (measured at the 4-digit ANZSIC level), and location (at the state level).
To calculate the effect of changes in composition of firms' age on the aggregate investment intensity, we need to weight the estimated age coefficients from our regression results by the share of output accounted for by firms of different ages. Doing so gives us a ‘weighted average age coefficient’ (WAAC). We construct this measure for pre- and post-GFC periods. The difference between the pre- and post-GFC WAAC can then be interpreted as the effect of ageing on the aggregate investment intensity, assuming that estimated age coefficients are constant across the two periods. Or more precisely,
Where,
- is firm age
- is age j's share of output in the post-GFC period (2012 to 2015)
- is age j's share of output in the pre-GFC period (2007 to 2008)
Appendix D
We use a Cobb-Douglas production function to analyse long-run investment intensity in the private non-mining market sector:
Where,
- is non-mining market sector output
- is non-mining market sector multi-factor productivity (MFP)
- is the non-mining market sector capital stock
- is non-mining market sector labour inputs
- is the labour share of income
In the steady state, the above equation becomes:[10]
Where,
- is non-mining market sector MFP growth
- indicates growth rates
- gives the steady state
Over our sample, technological progress seems to have been approximately “neutral” in the sense that it has not changed the capital-to-output ratio. This implies that the steady-state growth rate of both output and capital are equal. This implies that:
Where,
- is the exogenous growth rate of labour supply
We can now use the capital accumulation identity to relate the potential growth rate of output to the rate of investment. The capital accumulation identity is written as:
Where,
- is the non-mining market sector capital stock
- is non-mining market sector gross fixed capital formation
- is the depreciation rate
We can now use to give the long-run investment-to-output ratio:
We assume that in all periods, while all other values are taken directly from the annual national accounts.
Footnotes
The authors completed this work in Economic Analysis Department. We would like to thank Leon Berkelmans, Mark Chambers, Gianni La Cava, Peter Tulip and Michelle van der Merwe for helpful comments and feedback. [*]
See Appendix A for details on the adjustments we have made to the BLADE data prior to analysis. [1]
For evidence that the BLADE data are suitably comparable to the National Accounts data, see Appendix A. We consider changes in industry structure at the 4-digit Australian and New Zealand Standard Industrial Classification (ANZSIC) level. Details of the calculation can be found in Appendix B. [2]
More details on this model and its estimation are included in Appendix C. [3]
Even this is likely to be an overstatement of the role of ageing, given data coverage issues that we discuss in more detail in Appendix A. [4]
This section of the article is an update of previous internal RBA work by Leon Berkelmans and Gareth Spence. [5]
For details see Appendix D. [6]
In our model, the economy’s long-run investment intensity is calculated as the long-run (or potential) growth rate of output plus the depreciation rate, multiplied by the capital-to-output ratio. The ratio is surprisingly high, reflecting inconsistencies in the coverage of our investment, capital, and output measures. Nevertheless, this is unlikely to substantially affect the changes in the ratio, which tend to broadly track the observed non-mining investment-to-output ratio. [7]
The increase in coverage is also non-random in nature; for example, unincorporated firms make up just 5 per cent of firms born in 2000/01 but account for 51 per cent of new firms in 2001/02. [8]
Employment is measured as the number of full-time equivalent employees. [9]
As we focus on the long-run, we assume that the prices of investment goods, the capital stock, and output all grow at the same rate. Moreover, for ease of exposition we abstract from relative prices, and so the distinction between nominal and real quantities. [10]
References
Adeney R (2018), ‘Structural Change in the Australian Economy’, RBA Bulletin, March, viewed 6 June 2019.
CEA (Council of Economic Advisors) (2017), ‘Chapter 2: The Year in Review and the Years Ahead’, Economic Report of the President.
D'Arcy P and L Gustafsson (2012), ‘Australia's Productivity Performance and Real Incomes’, RBA Bulletin, June, pp 23–35.
Fernald J, R Hall, J Stock and M Watson (2017), ‘The Disappointing Recovery of Output after 2009’, Brookings Papers on Economic Activity, 2017(1), pages 1–81.
Jenner K, A Walker, C Close and T Saunders (2018), ‘Mining Investment Beyond the Boom’, RBA Bulletin, March, viewed 6 June 2019.
McCririck R and D Rees (2016), ‘The Slowdown in US Productivity Growth: Breaks and Beliefs’, RBA Research Discussion Paper No 2016-08.
Moreira, S (2017), ‘Firm Dynamics, Persistent Effects of Entry Conditions, and Business Cycles’, Center for Economic Studies, US Census Bureau.
Productivity Commission (2015), ‘Business Set-up, Transfer and Closure’, Inquiry Report, September.
Pugsley B, S Aysegul and F Karahan (2015), ‘Understanding the 30 year Decline in Business Dynamism: a General Equilibrium Approach’, 2015 Meeting Papers 1333, Society for Economic Dynamics.
van der Merwe M, L Cockerell, M Chambers and J Jääskelä (2018), ‘Private Non-mining Investment in Australia’, RBA Bulletin, June, viewed 6 June 2019.