Bulletin – June 2013 Financial Stability Mapping the Australian Banking System Network
- Download the article 2.2MB
Abstract
An important aspect of the banking system is the network of exposures between individual financial institutions. Using regulatory data, this article maps the network of large bilateral exposures between Australian financial institutions and then analyses its basic features using the tools of network theory. Many of the features of the Australian network are consistent with those of financial networks in other countries. In particular, most institutions in the network are only linked to a small number of other institutions, while a few, typically larger, institutions are linked to a large number of other institutions. An understanding of the banking system network can assist in identifying contagion risks and assessing financial stability.
Introduction
Many systems are composed of individual parts linked or connected in some way.[1] The pattern of these links can be represented as a network, that is, a set of nodes joined together in a particular way (Figure 1). Well-known examples are the internet and friendship networks. Studying complex systems as networks is useful because the particular pattern of connections – the structure of the network – can affect the behaviour of the whole system.[2] In particular, the complex interactions of the financial system can be modelled as a network where nodes represent financial institutions and links represent exposures between them.
This figure depicts a simple network consisting of a set of four nodes joined together with five links. The pattern of these links can be represented as a network.
The analysis of financial networks, though still in its infancy, is receiving increasing attention following the global financial crisis. For example, Haldane (2009) argues that the global financial system became increasingly complex and homogenous before the crisis, which increased its fragility as a network. From a financial stability perspective, network analysis can enhance policymakers' understanding of the interconnectedness of the financial system and its implications for the transmission of shocks and contagion.
This article presents an approximation to the network of exposures between Australian authorised deposit-taking institutions (ADIs) (banks, credit unions and building societies). While the data available are far from comprehensive, they highlight the basic features of the network.
Large Exposures
The available data provide a useful, albeit only partial, view of the bilateral exposures between financial institutions in Australia. These data are the ‘large exposures’ that ADIs report quarterly to the Australian Prudential Regulation Authority (APRA).[3] Smaller exposures are not individually reported to APRA and, therefore, are not available. Large exposures include on-balance sheet items such as loans or holdings of debt securities as well as off-balance sheet positions such as those related to financial derivatives.
Locally incorporated ADIs (including foreign-owned bank subsidiaries) are required to report their 10 largest exposures and all exposures that individually exceed 10 per cent of their regulatory capital. Foreign-owned bank branches, which do not hold capital locally, are required to report their 20 largest exposures. The exposures reported are to counterparties unrelated to the reporting ADI. For example, exposures of a foreign-owned bank in Australia to its overseas parent are excluded.[4]
In aggregate, ADIs reported large exposures to other Australian-owned ADIs and foreign-owned banks of about $210 billion as at December 2012 (or around 6 per cent of ADIs' aggregate consolidated group assets) (Table 1). On-balance sheet exposures comprised over two-thirds of the total, while off-balance sheet exposures, mostly interest rate and foreign exchange derivatives, represented less than a third. While the average large exposure was about $180 million, most large exposures were much smaller, with a median value of about $9 million, reflecting the fact that the majority of ADIs are small credit unions and building societies.
| On-balance sheet | Off-balance sheet | Total | |
|---|---|---|---|
| Major banks | 75 | 58 | 133 |
| Smaller Australian-owned banks | 23 | 2 | 25 |
| Foreign-owned banks | 39 | 5 | 44 |
| Credit unions and building societies | 9 | 0 | 9 |
| Total | 146 | 65 | 211 |
|
(a) Includes exposures of Australian-owned ADIs to the wider financial group of those foreign banks with subsidiaries or branches in Australia but excludes exposures to foreign banks that do not have a branch or subsidiary in Australia; exposures of foreign-owned banks in Australia to their wider financial groups are excluded Sources: APRA; RBA |
|||
More than half of outstanding ADI large exposures were to the four major Australian banks (Table 2). In part, this could reflect the ‘tiered’ nature of the inter-ADI market, where a small number of large banks transact with each other and a large number of small institutions place funds with the large banks. However, this also partly reflects the nature of large exposures reporting. If a large ADI and a smaller ADI have exposures to each other of a similar size, it is more likely that the smaller ADI's exposure to the larger one will qualify as a large exposure.[5]
| Lender | Borrower | Total | |||
|---|---|---|---|---|---|
| Major banks |
Smaller Australian banks |
Foreign- owned banks |
Credit unions and building societies |
||
| Major banks | 72 | 0 | 60 | 0 | 133 |
| Smaller Australian-owned banks | 15 | 3 | 6 | 0 | 25 |
| Foreign-owned banks | 28 | 3 | 13 | 0 | 44 |
| Credit unions and building societies | 3 | 5 | 1 | 1 | 9 |
| Total | 118 | 11 | 81 | 1 | 211 |
|
(a) Includes exposures of Australian-owned ADIs to the wider financial group of those
foreign banks with subsidiaries or branches in Australia but excludes
exposures to foreign banks that do not have a branch or subsidiary in
Australia; exposures of foreign-owned banks in Australia to their wider
financial groups are excluded Sources: APRA; RBA |
|||||
The foreign-owned banks are an important part of inter-ADI exposures both as borrowers and lenders (Table 2).[6] As borrowers, the foreign-owned banks represented about 40 per cent of ADIs' large exposures, partly because the data include exposures to the foreign-owned banks' wider international financial groups.[7] As lenders, the foreign-owned banks represented about 20 per cent of ADI large exposures. While this substantial share may arise in part because branches do not face local regulatory limits on the size of their exposures, it also reflects the fact that they are required to report their 20 largest exposures, compared with a minimum of 10 for other banks.[8]
Network Structure
The network of large exposures between Australian banks can be depicted graphically by representing banks as nodes and large exposures between borrowing banks and lending banks as links between nodes (Graph 1). The greater the number of links related to a given node, the closer the node is to the centre of the network. This network is ‘directed’, with links drawn as arrows flowing from borrowers to lenders, thereby indicating the possible path of contagion in case of financial distress of the borrower. The arrows are unweighted, indicating the existence of a link, but not its size, given that all exposures are large from the perspective of the lender. Additionally, the network is incomplete, since not all banks are directly linked to each other, and is disconnected, since there is one bank that is not linked to any other banks (at least via large exposures).
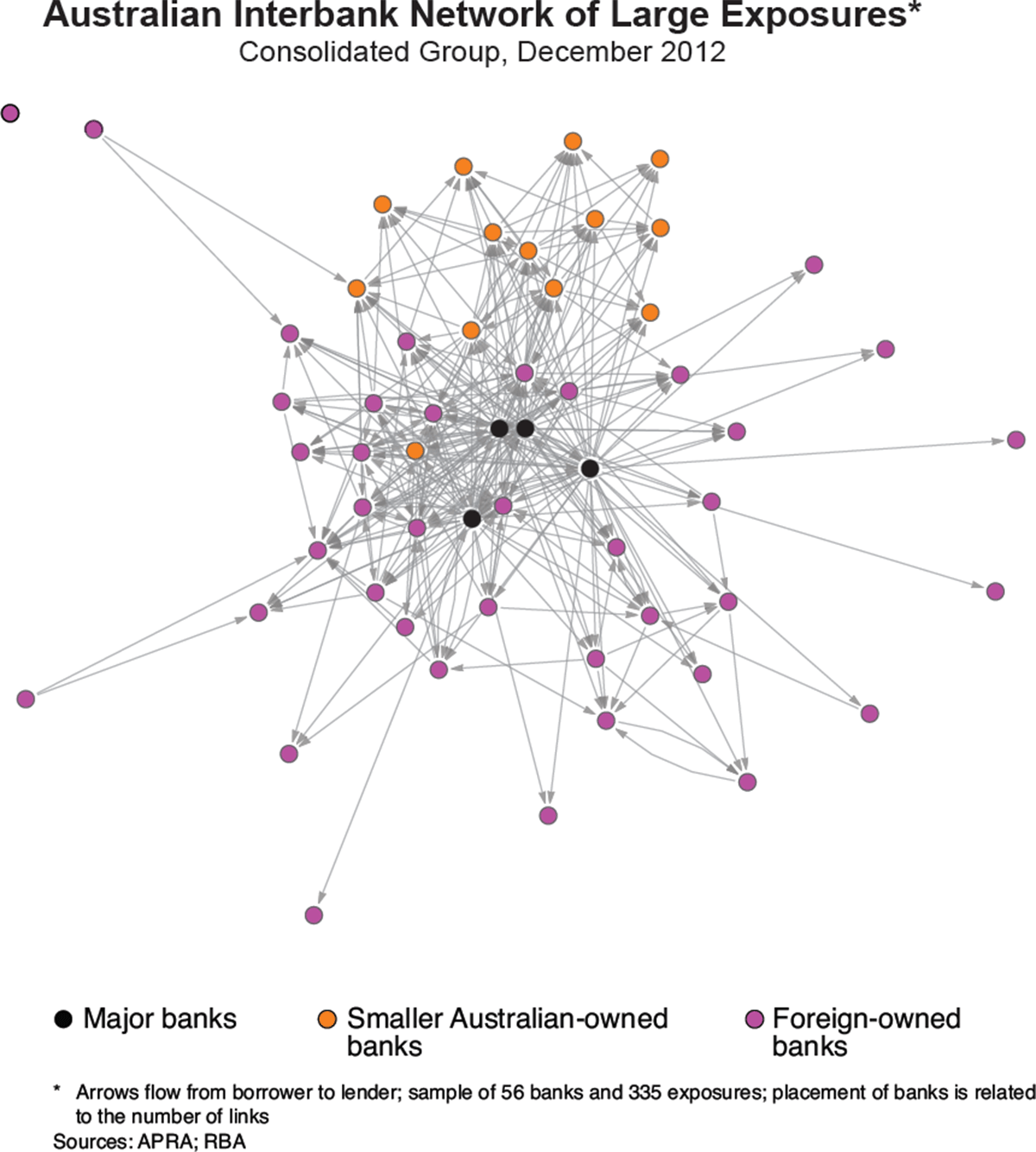
This depiction of the network highlights the fact that the major banks, which are placed at the centre of the graph, are linked to many other banks in the network. In contrast, most of the foreign and smaller Australian-owned banks are linked to only a few other banks. Also, the smaller Australian-owned banks tend to be more connected with other Australian-owned banks, while the foreign-owned banks tend to be more connected with other foreign-owned banks and the major banks.
This interbank network can be expanded by including the credit unions and building societies, which are generally smaller than the banks (Graph 2). In this more comprehensive depiction of the network, the major banks remain highly connected to other institutions, but some smaller institutions become highly connected as well. This graph illustrates the fact that, in the extended banking system network, the major banks tend to be more interconnected with the foreign banks and the smaller Australian-owned banks tend to be more interconnected with the credit unions and building societies.
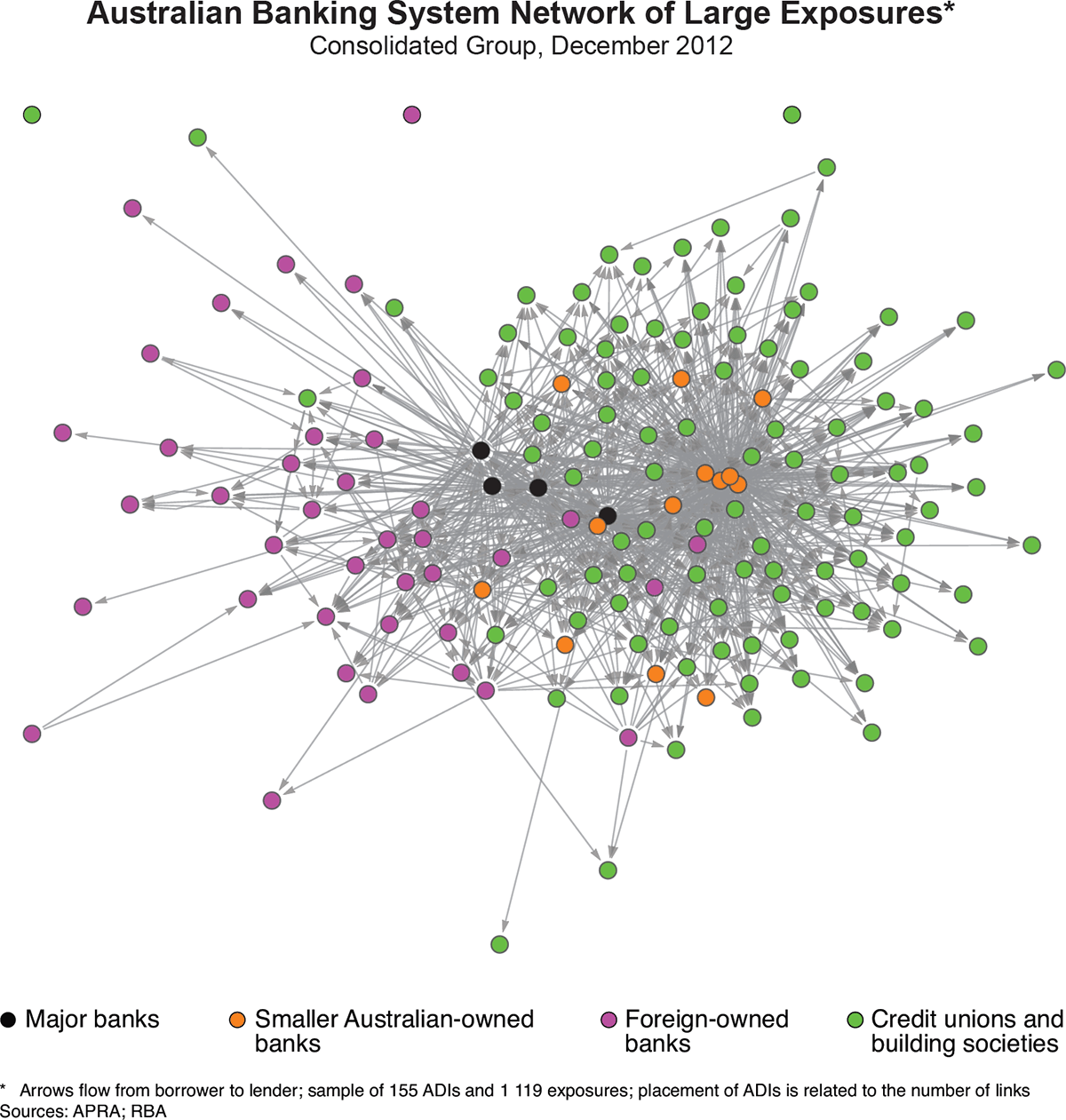
The visual representation of the network also highlights the complexity of the system of financial connections created by large exposures between ADIs. Despite this complexity, however, even the comprehensive version of the Australian banking system network is not very dense, with only about 5 per cent of all possible pairs of ADIs having direct links between them. Financial networks tend to have low density as they are generally comprised of a few well-connected institutions and a large number of sparsely connected institutions.[9] While the number of links between established institutions has tended to rise over the past few years, this has been offset by the entry of new institutions with few initial links, leaving the overall density of the network roughly unchanged.
Despite the low density of the network, about 30 per cent of pairs of ADIs are indirectly connected to each other through paths of links – that is, by following links according to the direction of the arrows. For example, if bank A borrows from bank B and bank B borrows from bank C, then there is a path of 2 steps in length between bank A and bank C. Across the network, these directed paths have an average length of 2.2 steps.[10] This small average ‘distance’ between pairs of nodes is a common feature of many networks and is generally known as the ‘small-world phenomenon’.[11] This effect can increase contagion in financial networks since a shock to a particular node can spread to many other (seemingly unrelated) nodes in only a few steps.[12]
The Degree of Centrality
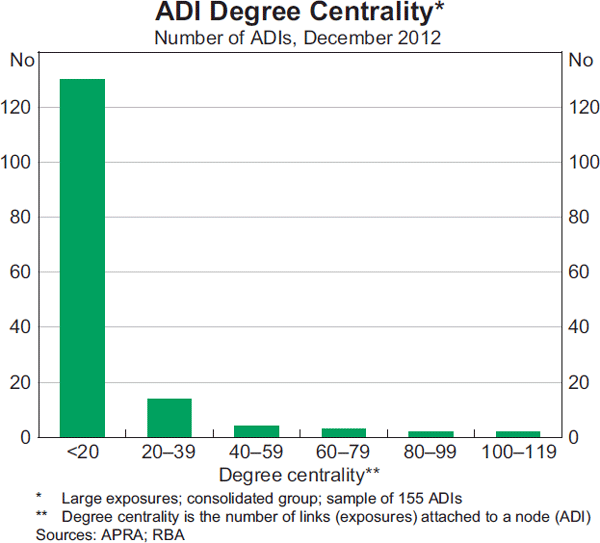
A key aspect of network analysis is to determine how important different nodes are in a network. A simple measure of importance is ‘degree centrality’, that is, the total number of links attached to a node, regardless of their direction. For a particular ADI, this includes links to institutions that it has borrowed from and links to institutions to which it has lent. Most ADIs in the Australian banking system network have low degree centrality, meaning that they are only linked to a few other institutions, while a few have very high degree centrality, with links to many other institutions. As at December 2012, the bulk of the sample of 155 ADIs had degree centrality below 20, while only a few had degree centrality greater than 100 (Graph 3).[13]
Larger ADIs tend to have higher degree centrality (more links) than smaller ones (Graph 4). This is not surprising because size can offer a number of advantages in a financial network. For example, larger institutions are more likely to have issued debt securities that are rated, which other institutions can hold for the purposes of investment or liquidity management. Nevertheless, there are a few smaller ADIs that have degree centrality much higher than their size would suggest. This high degree centrality mainly reflects many other smaller institutions placing funds with them either through direct deposits or purchases of debt securities. This is presumably because these deposits or securities offered more attractive yields than other comparable products in the market.
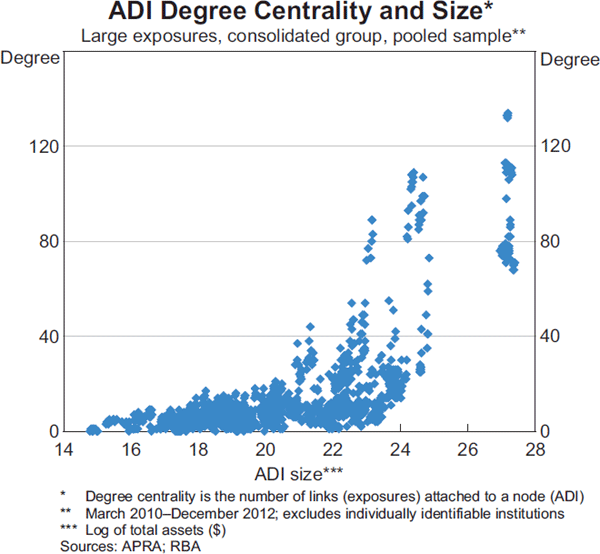
Differences in the Degree of Centrality
The extent of connections between ADIs implies that most are linked into the network in a minor way (low degree centrality), while a few ADIs have very extensive connections (high degree centrality). These large differences in degree centrality across institutions are usually illustrated using the rank-degree relationship, that is, the relationship between the rank of each institution and its degree centrality.[14] When plotted on a logarithmic scale, part of the rank-degree relationship appears to follow a straight line (Graph 5).[15] Broadly speaking, this indicates that, as an institution's ranking increases (moving down the line) its degree centrality increases disproportionately. Therefore, those institutions with the highest rankings (towards the lower end of the line) have degree centralities that are an order of magnitude greater than those institutions with the lowest rankings (towards the top end of the line). As a result, there are ADIs with degree centrality many times greater than that of the average ADI. For example, as at December 2012 the highest-ranked ADI had a degree centrality of 111, while the average degree centrality was about 14. Notably, the rank-degree relationship appears to follow a straight line at different points in time, suggesting that this is an enduring feature of the network.
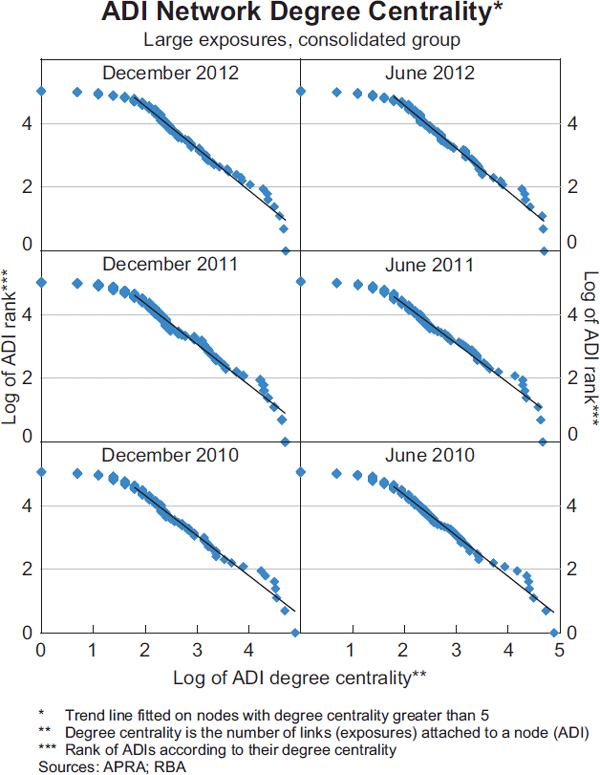
Empirical studies of financial and payments networks often find very large differences in the degree centrality of institutions.[16] These large differences are likely to arise from a ‘preferential attachment’ process, where the network grows by the addition of new nodes, which tend to attach themselves to existing nodes that are already well connected.[17] In a financial network, a new institution is likely to find it more advantageous to link to a well-connected bank that acts as a ‘hub’ for financial flows. Since connectivity is strongly correlated with size, a well-connected bank might offer services or products that other smaller, less-connected institutions do not. For example, larger banks usually offer derivative products that smaller institutions can use for hedging interest rate risk.
Networks with very large differences in the degree centrality of nodes generally exhibit a so-called ‘robust-yet-fragile’ property.[18] These networks are resilient to the failure of random nodes, since most of them do not have extensive connections, but they are very sensitive to the ‘targeted’ failure of the few nodes that are extensively connected. In a financial network setting, this suggests that the failure of an institution with minimal connections is less likely to generate contagion than the failure of an institution with extensive connections. In particular, the failure of an institution that has borrowed from many other institutions could generate losses across the system. However, this is mitigated by regulatory limits on large exposures, so the default by one institution should not by itself generate losses large enough to put its lenders in default.
Clustering
Many networks display transitivity – that is, if node A is linked to node B, and B is linked to C, then there is a relatively high probability that A and C are also directly linked.[19] Colloquially, a friend of my friend is also likely to be my friend. Groups of nodes that are highly interconnected, displaying high transitivity, are generally known as clusters.
A common measure of overall transitivity in a network is the global clustering coefficient. Broadly speaking, the coefficient relates the number of triangles in the network to the number of ‘open triangles’ (ignoring the direction of links).[20] For the Australian banking system network, based on large exposures, the global clustering coefficient is 0.22, meaning that if institution A is linked to institution B, and institution B is linked to institution C, then there is a 22 per cent probability that A is also directly linked to C.[21]
A related measure is the local clustering coefficient, which represents the average probability that any two of a node's neighbours – those nodes linked to it – are neighbours themselves (ignoring the direction of links). Intuitively, it quantifies how closely a node's neighbours approximate a complete sub-network. If a node's neighbours are all neighbours themselves, its clustering coefficient is one and if no links exist between them, the coefficient is zero. In the Australian banking system network, most institutions have a clustering coefficient between 0.5 and 0.8 with an average of about 0.6. Generally, this means that the neighbours of a node are themselves highly likely to be directly connected.
ADIs' local clustering coefficients are negatively correlated with their degree centrality (Graph 6). Institutions with low degree centrality (few links) tend to have neighbours that are extensively linked to each other (high clustering) while institutions with high degree centrality (many links) tend to have neighbours with sparse links to each other (low clustering). This occurs because nodes with large clustering coefficients belong to tightly knit groups, which are likely to be small. This inverse relationship between clustering and degree centrality has been relatively stable over time, suggesting that it is an enduring, structural feature of the network. The inverse relationship between clustering and degree centrality is also consistent with empirical findings for financial networks in other countries.[22]
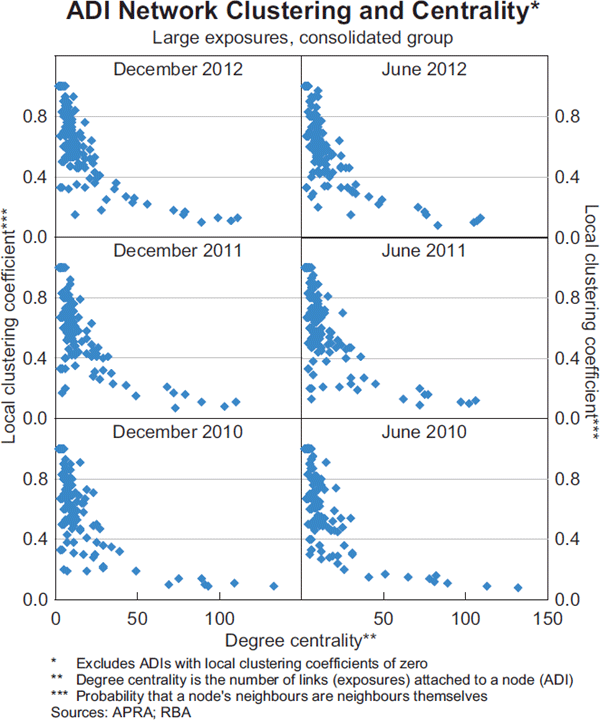
Conclusion
Financial institutions frequently interact with each other, for example, by borrowing from one another or entering into derivatives transactions. This generates complex interconnections that can be analysed using the tools of network theory. While the data available on large exposures of Australian ADIs provide only a partial view of these connections, they are still useful for understanding the general structure of the banking system network.
In the Australian banking system network, based on large exposures, only a small share of pairs of institutions have direct links between each other, although many pairs of institutions are indirectly connected to each other following paths of links. Consistent with the ‘small-world’ effect identified in many networks, these paths of links are, on average, very short.
Most institutions in the network are linked to a small number of other institutions, while a few institutions are linked to a large number of other institutions. This is likely to be the result of a process whereby new institutions that enter the network tend to form links with others that are already well connected. Since most institutions are only linked to a small number of other institutions, the network can be robust to random shocks, although it can be more sensitive to disruptions at the most connected institutions.
The Australian banking system network displays a relatively high degree of clustering, with institutions forming small subgroups that tend to be highly interconnected. As a result, the neighbours of an institution are highly likely to be connected among themselves. Since these subgroups of highly interconnected institutions are usually small, the institutions belonging to them are generally linked to only a few other institutions.
Many of the attributes of the Australian banking system network have also been identified in empirical studies of financial and payments networks in other countries. This suggests that there might be a common process underlying the evolution of financial networks in different countries.
Footnotes
The author is from Financial Stability Department. He would like to thank Luci Ellis for her contribution. [*]
The terms ‘links’ and ‘connections’ are used interchangeably in this article. [1]
See Newman (2010) for a comprehensive treatment of networks. [2]
The sample data used in this article include large exposures for banks, credit unions and building societies between March 2010 and December 2012. [3]
See APRA (2008). [4]
For example, most credit unions and building societies have total liabilities below 10 per cent of the major banks' regulatory capital. Therefore, it is very unlikely that a loan from a major bank to a credit union or building society will be considered as ‘large’ from the point of view of the major bank. [5]
The terms ‘lending’ and ‘borrowing’ are used in a general sense to include not just loans but also debt securities and derivatives transactions. [6]
In APRA's large exposures form, ADIs report the identity of their large exposures counterparties in a free-text field. Often, a counterparty is identified as an international banking group, but the location of the particular entity is not disclosed. For consistency, all exposures reported to foreign-owned banks (including those explicitly not in Australia) are attributed to the Australian entity if there is one. [7]
Locally incorporated ADIs are subject to a prudential limit of 50 per cent of their regulatory capital in their individual exposures to other ADIs. Exposures to individual non-ADI corporations and other businesses are limited to 25 per cent of capital. [8]
For example, studies for the Italian, Swiss and German interbank networks find ratios of actual connections to all possible connections of between 0.5 per cent and 1.5 per cent. However, these studies include a very large number of small credit institutions; for example, in the German case there are about 1200 credit unions in the sample. See Müller (2003), Lazzeta and Manna (2009) and Craig and von Peter (2010). [9]
There can be many possible different paths between two nodes. The average is based on the shortest path between each pair of nodes. [10]
The small-world phenomenon, also known as the ‘six degrees of separation’, was the object of experimental studies about social networks in the United States in the 1960s (see Milgram 1967). [11]
Similarly, infectious diseases are predicted to spread more quickly in small-world networks (see Watts and Strogatz 1998). [12]
High centrality reflects ADIs' borrowing (out-degree) more so than lending (in-degree), particularly for those institutions with the highest centrality. The high out-degree arises from an institution being reported by many other different institutions as a large exposure. In contrast, the low in-degree centrality mostly reflects the fact that, in general, ADIs only report their 10 largest exposures (20 for foreign-owned branches). [13]
The rank is simply calculated by sorting institutions by their degree centrality. The institution with the highest degree centrality has a rank of one, the institution with the second highest degree centrality has a rank of two and so on. [14]
Distributions that follow this pattern are generally known as ‘power laws’ (see Clauset, Shalizi and Newman 2009). [15]
For example, see Boss et al (2004), Soramäki et al (2006) and Bastos e Santos and Cont (2010). [16]
See Barabási and Albert (1999). [17]
See Albert, Jeong and Barabási (2000). [18]
The probability is high relative to that of a network with the same number of nodes and links, where the links are randomly allocated across nodes (see Newman 2010, p 200). [19]
A triangle is a set of three nodes connected by three links. For simplicity, the term ‘open triangle’ is used to refer to connected triples, that is, three nodes that are connected by two links. The global clustering coefficient is three times the ratio of the number of triangles to the number of connected triples (for more details, see Newman 2010, p 200). [20]
For a comparably sized random network with the same number of nodes and links, the global clustering coefficient converges to around 9 per cent. [21]
For example, see Bastos e Santos and Cont (2010) for the Brazilian case. More generally, this is also a property observed in many non-financial networks (see Newman 2010, p 265). [22]
References
Albert R, H Jeong and AL Barabási (2000), ‘Error and Attack Tolerance of Complex Networks’, Nature, 406, pp 378–382.
APRA (Australian Prudential Regulation Authority) (2008), ‘Reporting Form ARF 221.0 – Large Exposures – Instruction Guide’, February.
Barabási AL and R Albert (1999), ‘Emergence of Scaling in Random Networks’, Science, 286(5439), pp 509–512.
Bastos e Santos E and R Cont (2010), ‘The Brazilian Interbank Network Structure and Systemic Risk’, Banco Central do Brasil Working Paper No 219.
Boss M, H Elsinger, M Summer and S Thurner (2004), ‘The Network Topology of the Interbank Market’, Quantitative Finance, 4, pp 677–684.
Clauset A, CR Shalizi and MEJ Newman (2009), ‘Power-law Distributions in Empirical Data’, SIAM Review, 51, pp 661–703.
Craig B and G von Peter (2010), ‘Interbank Tiering and Money Center Banks’, Bank for International Settlements Working Paper No 322.
Haldane A (2009), ‘Rethinking the Financial Network’, Speech delivered at the Financial Study Association, Amsterdam, 28 April.
Lazzeta C and M Manna (2009), ‘The Topology of the Interbank Market: Developments in Italy since 1990’, Banca d'Italia Temi di Discussione No 711.
Milgram S (1967), ‘The Small-World Problem’, Psychology Today, 1(1), pp 61–67.
Müller J (2003), ‘Identifying Systemic Risk in the Swiss Interbank Market – A Network Analysis’, Swiss National Bank Draft Working Paper.
Newman MEJ (2010), Networks: An Introduction, Oxford University Press, New York.
Soramäki K, ML Bech, J Arnold, RJ Glass and WE Beyeler (2006), ‘The Topology of Interbank Payment Flows’, Federal Reserve Bank of New York Staff Report No 243.
Watts DJ and SH Strogatz (1998), ‘Collective Dynamics of “Small-World” Networks’, Nature, 393(6684), pp 440–442.