Bulletin – December 2013 Australian Economy Realisation Ratios in the Capital Expenditure Survey

Introduction

Business investment reached 18 per cent of output in the second half of 2012, its highest share in over 50 years. This share has since declined and is expected to continue to decline, although by how much and over what period is unclear.

The Reserve Bank uses a variety of sources of information to guide its forecasts of business investment (Connolly and Glenn 2009). One potentially useful source is the quarterly Australian Bureau of Statistics capital expenditure survey (Capex survey). This survey provides expectations of capital expenditure for up to 18 months ahead, with breakdowns available by industry and type of asset.

The expectations of capital expenditure are, naturally, subject to a degree of uncertainty, and final outcomes can differ substantially from earlier expectations. In other words, sometimes more or less of the earlier expected investment is realised. This article examines these errors in the investment expectations component of the survey, and considers the best method of adjusting the raw expectations in order to minimise these errors. Out-of-sample forecasting exercises indicate that adjusting for long-run bias appears worthwhile, but further adjustments that attempt to use information on the state of the business cycle are not. The ability of these forecasts to predict investment in the national accounts is also considered, with mixed results.

The Capex Survey

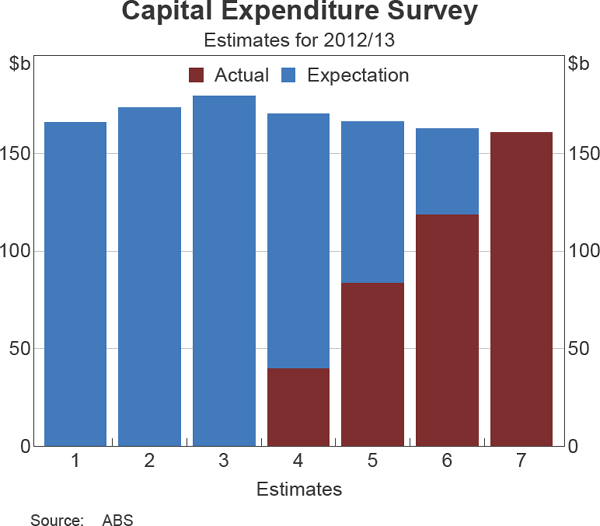
The Capex survey provides information on actual capital expenditure in the most recent quarter, along with firms' capital expenditure expectations. The expectations component of the survey is one of the few sources of information that quantifies the value of firms' expected investment. These expectations provide capital expenditure estimates for up to 18 months into the future in a series of observations for any given financial year. The expectations for each financial year are updated for five successive quarters after the initial estimate, providing a series of six estimates of expected capital expenditure for each financial year. The fourth and higher estimates are made after some of the year has elapsed, so these estimates include some expenditure that has already occurred. As an example, the December quarter 2011 Capex survey provided the first estimate of firms' expectations for capital expenditure for 2012/13, while the September quarter 2012 survey, which provided the fourth estimate, was the first to include some actual data for that financial year (Graph 1).

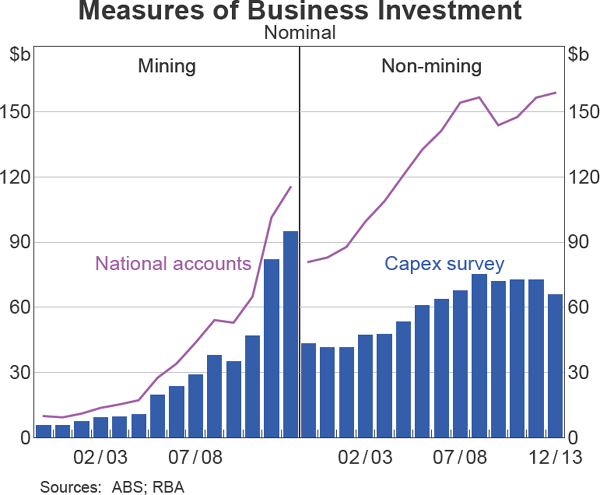
Details for both the actual and expected components of the survey are not available for every industry in the economy; only 15 of the 19 industries included in the national accounts are covered by the Capex survey. Also, the survey only covers expenditure on machinery & equipment and buildings & structures. Other business assets covered by the national accounts, such as research and development, are excluded. As a result of these differences in coverage of assets and industries, the value of the investment measured in the Capex survey is below that of the national accounts, particularly in the industries outside of mining, and the growth rates of the series can also differ substantially (Graph 2).

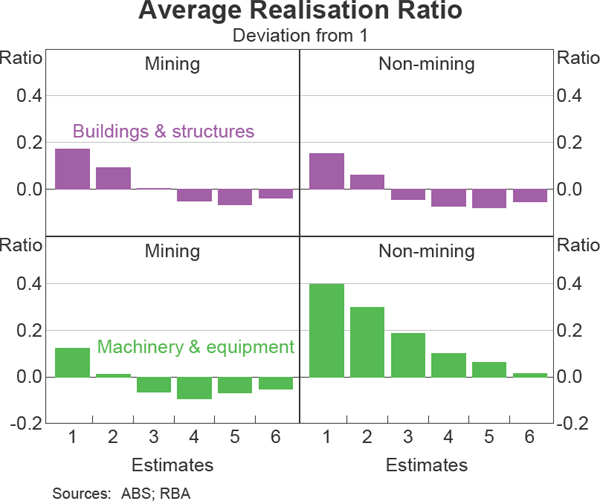
Nonetheless, the expectations component of the Capex survey remains a potentially useful starting point for assessing the outlook for investment, given that it provides a dollar value of expected expenditure which is not generally available in other business surveys. Project-based databases such as the Deloitte Access Investment Monitor and the Bureau of Resources and Energy Economics major projects list provide the expected value of each project but do not provide a profile of spending for each project, and also only include a subset of all projects underway. The raw expectations from the Capex survey, naturally, will differ from the actual expenditure for that year for a number of reasons. The degree to which the expectations differ from the final outcome can be assessed by the ‘realisation ratio’ of the estimate; realisation ratios are the actual expenditure divided by the expected expenditure. If the estimates were unbiased, the average realisation ratio would be close to one, given a long enough sample. Many of the expectations, however, have an average realisation ratio greater than one (Graph 3). This is particularly pronounced for non-mining machinery & equipment, where final expenditure has been on average 30–40 per cent above the early estimates. Moreover, small firms' estimates suffer from more downward bias than large firms (Burnell 1994). There are several plausible explanations for these biases. For example, in forming their expectations, firms may not account for the expenditure required to replace existing machinery and equipment that depreciates. In addition, the investment planning horizon for small businesses may be relatively short, leading these firms to underestimate their expenditure over a year in advance, particularly if they only report expenditure that they are relatively certain they will undertake. It also appears that in some industries, later estimates of expenditure overestimate the final outcome. This possibly reflects the fact that once required expenditure is identified or new plans are made, firms are unable to undertake this expenditure at a short horizon. In any case, it appears necessary to adjust the raw expectations of the survey to account for the biases, and thereby produce more accurate forecasts of investment.

Methods of Adjustment

The adjustment of the raw expectations can be implemented by multiplying the raw estimate by an expected realisation ratio based on historical experience or other information. A simple method that would help to eliminate bias would be to use the historical long-run average realisation ratio. However, additional methods of realisation ratio projection may be appealing, particularly if the degree of bias is not stable over time. One option to capture any time-varying bias is to use a realisation ratio based on the average of the previous five years; indeed, the ABS reports the five-year ratio when they publish the results from the Capex survey. Another alternative is to use the previous year's realisation ratio.

Regression-based approaches may also be used to project realisation ratios to take account of how the expectation error could vary over time or in relation to other variables. A simple autoregressive model with one lag (i.e. an AR(1)) is an obvious starting point, but other variables may be added. For example, some measure of the business cycle could be useful, as there is some evidence that the realisation ratio varies systematically with economic activity (Cassidy, Doherty and Gill 2012). A timely indicator of the business cycle that would be suitable for this purpose is the measure of business conditions from the NAB quarterly survey. It is important, however, to be clear what this business cycle adjustment is supposed to be addressing. The business cycle would already be affecting firms' raw expectations. Further conditioning the realisation ratio on the state of the business cycle is an attempt to allow the difference between firms' capital expenditure expectations and actual outcomes to also be affected by economic activity.

These five methods of realisation ratio adjustment – the long-run average, the five-year average, the previous-year ratio, a simple AR(1) regression approach and an AR(1) regression augmented with the NAB survey measure of business conditions – are tested for out-of-sample accuracy.^[1] The long-run average approach performs best over the sample period (Graph 4 and Graph 5).^[2] For each of the four key aggregates which the Bank monitors – mining and non-mining capital expenditure for both machinery & equipment and buildings & structures – the long-run average generally outperforms the other methods of realisation ratio adjustment across most of the six estimates. In line with Cassidy, Doherty and Gill (2012), the accuracy of the forecasts improves as the estimates get closer to the actual time period under consideration (i.e. as the estimate number increases).

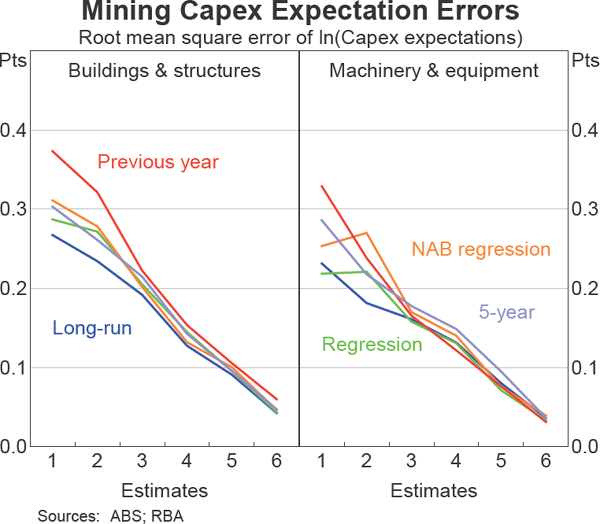
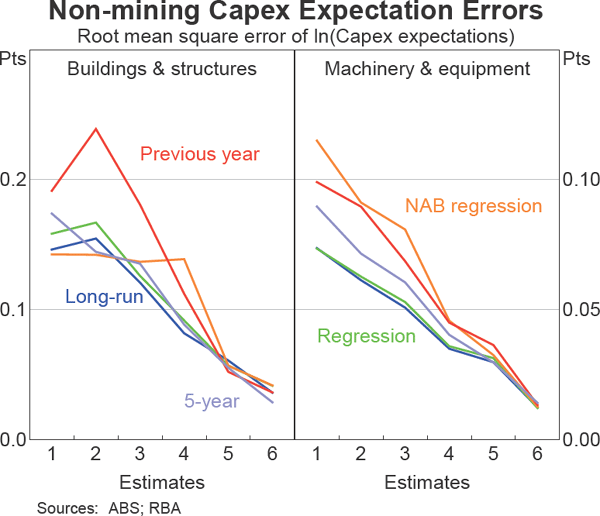
The superior performance of the long-run average approach suggests that other methods may lead to problems of over-fitting within sample, with little apparent benefit when it comes to forecasting out of sample. For example, while there is evidence that the realisation ratio is correlated with economic conditions, this correlation does not seem to be something that can be exploited for forecasting purposes. It may be that the correlation arises because the realisation ratio is affected by changes in economic conditions that are only apparent after firms are surveyed, so using the conditions at the time of the survey does not add any value.

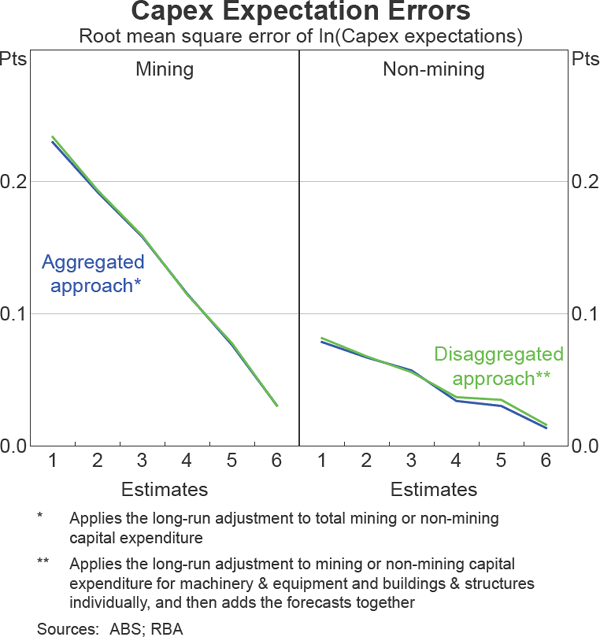
The Bank also considers expected capital expenditure data at a more aggregated level. For example, the Statement on Monetary Policy often refers to mining and non-mining investment. It is worth asking whether these aggregates are forecast by applying the same technique as above to the aggregates, instead of adding the disaggregated forecasts together. The results indicate that there is very little difference between these approaches, and so for ease of exposition it seems reasonable to forecast aggregates based on the addition of the disaggregated forecasts (Graph 6).

The Distribution of Forecast Errors

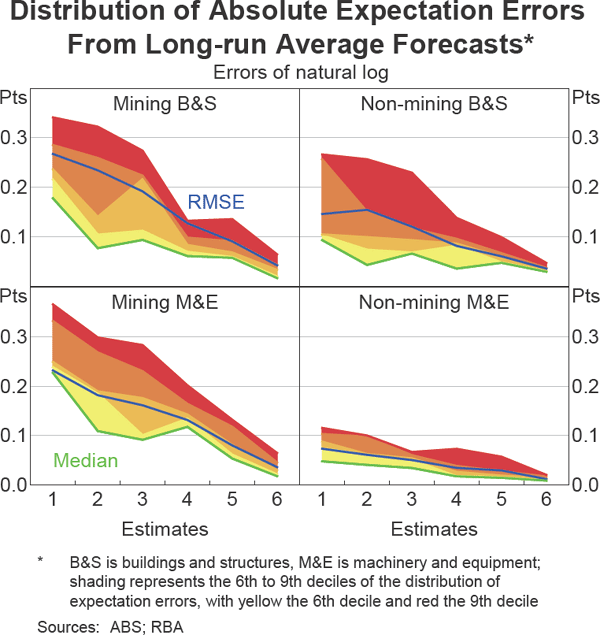
In the November 2013 Statement on Monetary Policy the Bank published error bands around the capital expenditure estimates associated with the long-run average technique (that are two root mean square errors (RMSEs) in width). It is useful to know what kind of uncertainty these error bands correspond to, which may be gauged by considering where the RMSE lies in the distribution of absolute errors. The RMSE for machinery & equipment capital expenditure often lies in the 60–70th percentile of the distribution, so the error bands can be considered as corresponding to a rough 60–70 per cent prediction interval (Graph 7).^[3] The RMSE for the buildings & structures estimates sit higher at around the 70–80th percentile, pointing to a few relatively large misses in the past. For example, the adjusted forecast from the first estimate for 2005/06 mining buildings & structures capital expenditure was less than half that of the final outcome.

Relationship with National Accounts Investment

In developing an outlook for the domestic economy, it is desirable to have a forecast for total business investment, as measured by the national accounts, not just those components captured by the Capex survey. While there are coverage issues associated with the Capex survey when compared with the national accounts, the survey's appeal lies in its explicit quantification of firms' capital expenditure expectations. Moreover, the actual investment outcomes in the Capex survey are an input into the national accounts, so there is also a direct link which could make the expectations data useful. The Capex survey's utility for forecasting the national accounts measure of investment was assessed using out-of-sample forecasts. The implied growth of mining and non-mining investment from the survey is compared with the actual outcomes in the national accounts. The accuracy of these forecasts is assessed against the accuracy of out-of-sample forecasts arising from information only included in the national accounts. The national accounts based forecast is the historical average growth (excluding the previous year, which is not available at the time of the early estimates from the Capex survey used in this exercise).^[4] Alternative methods were considered, such as simple regression approaches, but the results were little changed. For mining investment, the out-of-sample forecasts based on the Capex survey are more accurate, having a lower RMSE, than those based on the historical growth in the national accounts. For non-mining investment, the Capex-based forecasts are more accurate for estimates later than the third estimate for non-mining investment (Graph 8).^[5] The more favourable results for mining than non-mining using Capex-based forecasts may reflect the fact that the Capex survey has a greater coverage of the mining sector than it does of the non-mining sector. It could also be that the boom in mining investment over recent years means that the past has been a relatively poor guide for the future, whereas the capital expenditure has picked up the boom to a better extent.

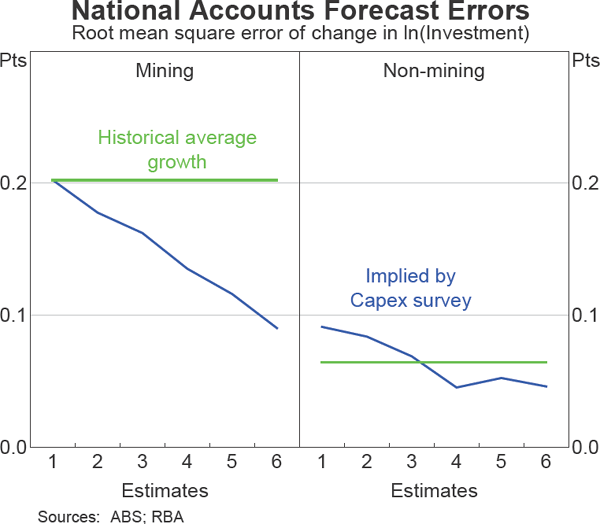
The results for mining investment are encouraging, although it should be noted that the RMSE for mining investment is much larger than for non-mining investment. That is, while the Capex survey seems to add some information over and above the average historical growth in investment in the national accounts, forecasts arising from the Capex survey are still relatively inaccurate. The non-mining results are disappointing. The first three estimates of the Capex survey do not seem, by themselves, to provide better information than a simple historical average. Later estimates do provide an improvement, but this is not a fair comparison, since from the fourth Capex estimate onwards, the expectations include some actual capital expenditure data for that financial year. To get a true indication of the extra information in the Capex survey, further work is required, which may involve using quarterly national accounts data and the short-term expectations included in the Capex survey.

Conclusion

The results in this article show that capital expenditure realisation ratios based on long-run averages are generally preferable to various alternatives. For the more aggregated measures that the Bank frequently considers, forecasts based on the addition of the disaggregated series are just as accurate as forecasts derived directly from the aggregated series. Nonetheless, judgement is required when interpreting these forecasts, given the relatively poor performance of these expectations in forecasting non-mining investment in the national accounts. Moreover, when forecasting total investment in both the mining and non-mining sectors, the Bank relies on a broader set of information, including from its liaison program. The Bank will continue monitoring the forecasting performance of these methods as more data become available.

Footnotes

The authors completed this work in Economic Analysis Department. [*]

These forecasting exercises are based on the difference between the natural logarithm of the forecast and the natural logarithm of the outcome. These series increase at an exponential rate, so the natural logarithm is the appropriate way to evaluate the forecast. [1]

These exercises were based on out-of-sample forecasts beginning at the point at which 11 years of data informed the first forecast. The data begin for the financial year 1987/88 or 1988/89, depending on the estimate number. [2]

This assumes that there is no bias to the forecasts and that the errors are symmetric. [3]

Data from 1960 were used to form the long-run average. The current vintage of data was used for all calculations. [4]

These calculations are based on assuming that the previous year's expenditure from the Capex survey is known at the time that estimates one and two are provided. This is in fact not the case, and so these calculations may understate the true RMSE arising from forecasts based on estimates one and two. [5]

References

Burnell D (1994), ‘Predicting Private New Capital Expenditure Using Expectations Data’, Australian Economic Indicators, ABS Cat No 1350.0, January, pp xi-xvii.

Cassidy N, E Doherty and T Gill (2012), ‘Forecasting Business Investment Using the Capital Expenditure Survey’, RBA Bulletin, September, pp 1–10.

Connolly E and J Glenn (2009), ‘Indicators of Business Investment’, RBA Bulletin, December, pp 18–27.