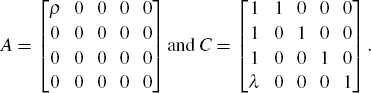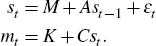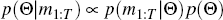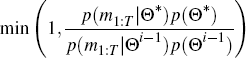RDP 2014-12: A State-space Approach to Australian GDP Measurement 3. Estimation
October 2014 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 904KB
We follow the approach of Aruoba et al (2013) and estimate the models within a Bayesian framework. We work with Model 3 in this section; Models 1 and 2 are nested in Model 3 and can be recovered by setting appropriate parameters to zero.
First we express our model in state-space form. Let st = [Δyt, εE,t,
εI,t, εP,t,
εU,t]′, 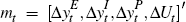 , M = [μ(1 − ρ),0,0,0,0]′,
K = [0,0,0,κ], εt = [εG,t,
εE,t, εI,t,
εP,t, εU,t,]′,
, M = [μ(1 − ρ),0,0,0,0]′,
K = [0,0,0,κ], εt = [εG,t,
εE,t, εI,t,
εP,t, εU,t,]′,
Then we can then express Model 3 as
For ease of notation, we collect the parameters in the vector
Θ = 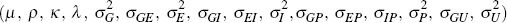 .
.
We use the Metropolis-Hastings Markov Chain Monte Carlo (MCMC) algorithm to estimate model parameters.[9] We first maximise the posterior distribution of Θ given the observed data
where p(m1:T |Θ) is the density of the observable data given the model parameters and p(Θ) is the density of the priors over the parameter draw. This gives us an initial estimate of Θ, denoted Θ0. We use the inverse Hessian at the maximum to obtain an estimate of the covariance matrix of Θ, Σ0. Θ0 and Σ0 are then used to initiate the MCMC algorithm: at each iteration i we draw a proposed parameter vector Θ* ∼ N(Θi−1, cΣi−1). Here c is a scaling parameter set to achieve an acceptance rate of around 25 per cent, where we accept Θ* as Θi with probability
and set Θi = Θi−1 otherwise. We set p(Θ*) = 0 if Θ* is not a valid draw, for example if it implies a covariance matrix that is not positive definite.
In order to sample Θ* from the N(Θi−1, cΣi−1) distribution we need to evaluate p(m1:T|Θ). To do this we use the standard Kalman filter and simulation smoother, as described in Durbin and Koopman (2012). We take 50,000 draws from the posterior distribution and discard the first 25,000.
3.1 Priors
Our prior for the mean growth rate of GDP, μ, follows a normal distribution with mean 0.80 and standard deviation 10.[10] The mean of this prior corresponds to the average quarterly growth rate of GDP over our sample while the standard deviation is extremely large relative to the volatility of the GDP series, indicating that this prior places only a very weak restriction on the range of potential values. For the persistence of shocks to GDP growth, ρ, we use a beta prior with mean 0.50 and standard deviation 0.20. The prior restricts the value of this parameter to lie between 0 and 1, consistent with GDP growth being a stationary series.[11]
For the variances of the shocks to GDP and the measurement errors, we impose inverse-gamma priors with mean 2 and standard deviation 4. These priors ensure that the variances of all shocks are greater than 0. Finally, for the covariance terms, the priors follow a normal distribution with mean 0 and standard deviation 5.
In all cases, our priors are loose, ensuring that we place a large weight on information from the data, but rule out unreasonable parameter values.
3.2 Data
Our data span 1980:Q1–2013:Q2. The starting date reflects the fact that, while Australian national accounts data are available on a quarterly basis from 1959:Q3, the quality of the underlying data sources has changed over time, so that the pattern of measurement errors in the early years of each GDP series may be unrepresentative of their current performance. The GDP and unemployment rate data that we use in our estimation are all seasonally adjusted by the ABS.
Footnotes
See An and Schorfheide (2007) for a description of these techniques. [9]
Our estimation procedure assumes that the trend growth rate of GDP has been constant over our sample. To test whether this assumption is reasonable, we ran Bai-Perron tests for a break in the mean growth rate of GDP(A) using an AR(1) model over the sample 1980:Q1–2013:Q2. These tests did not point to any evidence of a break in the mean growth rate of GDP(A) over our sample. [10]
Imposing a normally distributed prior with a mean of zero produces almost identical results. [11]