Bulletin – March 2010 Measures of Underlying Inflation
- Download the article 147KB
Abstract
Various measures of underlying inflation are used at the Reserve Bank. These measures are useful in assessing current inflation pressures in the economy as well as the outlook for future movements in the consumer price index.
Introduction
In Australia the inflation target is expressed in terms of the average rate of increase in the consumer price index (CPI). In particular, the objective is to ensure that the rate of increase in the CPI averages between 2 and 3 per cent over the medium term. In assessing current inflation pressures and the outlook for CPI inflation, the Reserve Bank makes use of a wide range of measures of ‘underlying’ inflation which attempt to abstract from the short-term volatility in some prices. This article discusses the various measures of underlying inflation and the role of these in forecasting and analysis at the Bank.[1]
Measures of Underlying Inflation
Quarterly movements in the ‘headline’ CPI series can be volatile. This volatility reflects price changes in particular items that may be due, among other factors, to fluctuations in commodity markets and agricultural conditions, policy changes, or seasonal or infrequent price resetting. An example was the movement in banana prices in mid 2006 because of the supply disruption caused by Cyclone Larry. Following the cyclone, prices of bananas increased by around 400 per cent, before falling by almost 80 per cent by early 2007, with these movements first adding and then subtracting about ¾ percentage point to the rate of inflation. Movements in oil prices also often have a significant effect on CPI inflation. For example, over 2005–2009, the average absolute quarterly change in the price of automotive fuel (petrol, diesel and LPG) was just over 6 per cent, which implied an average contribution or subtraction to CPI inflation of over ¼ percentage point per quarter.
While some large changes in the prices of particular items will contain information about the future trend in inflation, as an empirical matter much of the quarter-to-quarter movement in the CPI tends to be temporary. Accordingly, central banks attempt to assess the ‘underlying’ rate of consumer price inflation, both to better understand the current trend in inflation and assist in forecasting medium-term inflation.
While underlying inflation is neither an observable variable nor precisely defined, at a conceptual level it is usually thought of as the ‘persistent’ or the ‘generalised’ component of inflation. There are many ways to estimate underlying inflation, but the two approaches most commonly used by central banks are ‘exclusion-based’ measures and trimmed-mean measures.[2]
Exclusion-based measures
Traditionally, the most widely used exclusion measure in Australia has been the inflation rate for the CPI basket excluding a particular set of volatile items – namely fruit, vegetables and automotive fuel. The rationale for excluding the direct effect of those items is that their prices tend to be volatile and often do not reflect underlying or persistent inflation pressures in the economy.
Recently the Bank has been publishing a series for inflation that also excludes the deposit and loan (D&L) facilities expenditure class within the CPI. This item attempts to capture the price of the financial intermediation service that financial institutions charge for D&L facilities, but it has been subject to some measurement problems and recently has been affected by the large changes in the structure of interest rates resulting from the turmoil in financial markets over the past two years or so. Furthermore, movements in the D&L facilities index have tended to be positively correlated with movements in the cash rate, which would suggest an additional rationale for its exclusion from a measure of underlying inflation used in the monetary policy process.
There are, however, circumstances when exclusion-based measures do not provide especially good estimates of underlying inflation. These can arise when there are large temporary movements in components of the CPI that are not excluded from such measures. In addition, in some cases information about underlying inflation pressures can be lost when the ‘volatile’ components are excluded. For example, a measure of inflation that always omits automotive fuel prices may be smoother, but through much of the past decade might have understated overall inflation pressures as global oil prices trended up because of strong growth in global demand.
Trimmed-mean measures
Trimmed-mean measures of underlying inflation represent an alternative approach and are used in a number of central banks. The trimmed-mean rate of inflation is defined as the average rate of inflation after ‘trimming’ away a certain percentage of the distribution of price changes at both ends of that distribution. These measures are calculated by ordering the seasonally adjusted price changes for all CPI components in any period from lowest to highest, trimming away those that lie at the two outer edges of the distribution of price changes for that period, and then calculating an average inflation rate from the remaining set of price changes.
Different degrees of trimming are possible and will provide different estimates of underlying inflation. In practice, the Bank has tended to focus on two particular trims: the 15 per cent trimmed mean (which trims away the 15 per cent of items with both the smallest and largest price changes) and the weighted median (which is the price change at the 50th percentile by weight of the distribution of price changes). Since 2007, the Australian Bureau of Statistics (ABS) has published these two series, calculated according to the methodology used by the Bank.
The rationale for trimmed means is that there are sometimes very large changes in prices for particular items that have a significant effect on a conventional average of all price changes, but which are quite unrepresentative of price changes of other goods and services. Whereas exclusion measures remove some pre-specified items in every period regardless of whether or not their price changes are extreme, trimmed-mean measures down-weight the impact of items in a given period if their price changes are ‘unrepresentative’ in the period in question.[3] Accordingly, these series provide an estimate of the central tendency of the distribution of price changes that is less affected by large price changes – either increases or decreases – in individual items.[4]
Empirical work at the Bank using data for Australia, the United States, the euro area and Japan has shown that trimmed-mean estimates perform well on a number of criteria (see Brischetto and Richards 2007). In particular, trimmed-mean measures appear to have a higher ‘signal-to-noise’ ratio than the CPI or some exclusion-based measures, which makes them useful in assessing ongoing inflation pressures in the economy.
Notwithstanding this, one finding from the Bank's research is that trimmed-mean estimates can be affected by the presence of expenditure items with very large weights in the CPI basket (see Brischetto and Richards 2007). Such large items make the distribution of price changes less smooth, which can add volatility to trimmed-mean measures, especially to the weighted median. This issue is particularly relevant in the United States, where the weight for ‘implicit rent for home owners’ is close to a quarter of the overall CPI. Research has shown that breaking this item up geographically into four regional sub-components provides a somewhat smoother distribution of price changes that is less prone to large peaks. The result is an improvement in the usefulness of trimmed-mean estimates of US inflation, especially in the case of the weighted median.[5]
While the Australian CPI is much less subject to problems of this nature,[6] the existence of CPI data for the eight capital cities allows the calculation of trimmed-mean inflation using more disaggregated data – namely 720 city-level price changes rather than 90 nationwide-average price changes. This results in a somewhat smoother distribution of price changes, as shown by the data for the December quarter of 2009 (Graph 1).[7]
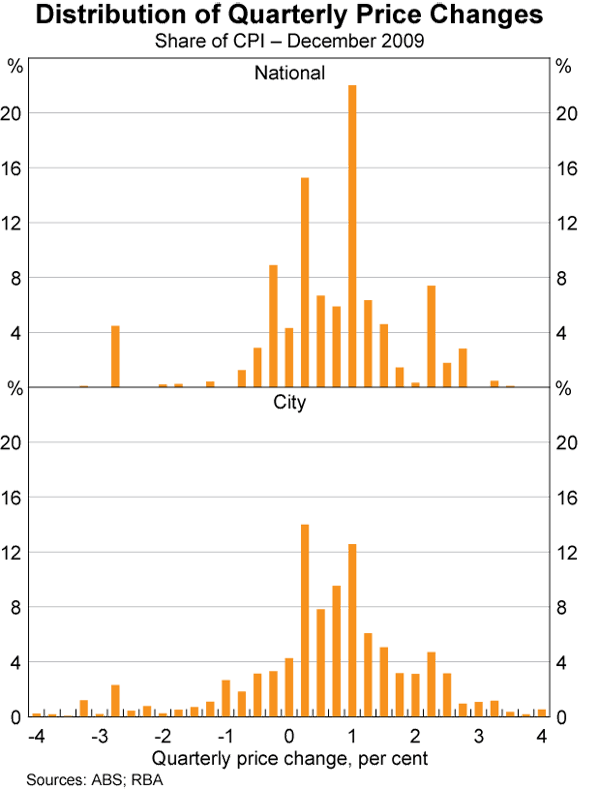
As is the case with the US data, the use of a finer level of detail of price changes has a relatively limited effect on estimates of the 15 per cent trimmed mean but a more significant effect on estimates of the weighted median. For example, over 2001–2009, the average absolute difference between trimmed-mean inflation calculated using the different approaches was just 0.04 percentage points, versus 0.10 percentage points for the weighted median. In the December quarter 2009, quarterly trimmed-mean inflation was estimated at 0.57 per cent based on national data and 0.58 per cent for city-based data, whereas weighted-median inflation based on the city-based data was 0.55 per cent, compared with 0.69 per cent for the national measure.[8] Overall, based on the US evidence and staff analysis using Australian data, the use of city-level data appears to be a useful alternative to the use of national data.
Another technical issue in the calculation of trimmed-mean inflation is that year-ended underlying inflation can be based on either quarterly or annual price changes. The year-ended series published by the Bank and the ABS have typically been based on quarterly price changes, whereby quarterly rates of underlying inflation are first calculated, with the annual rate of underlying inflation based on the cumulated quarterly rates.[9] An alternative is to calculate year-ended trimmed-mean inflation based on the distribution of year-ended price changes. Previous empirical work has suggested that year-ended data should not be used in the case of large trims, such as the weighted median (see Brischetto and Richards 2007). However, for smaller trims, such as the 15 per cent trim, there do not seem to be strong reasons to prefer one approach over the other for calculating year-ended trimmed-mean inflation. Accordingly, Bank staff calculate year-ended trimmed-mean inflation using both methods.
Recent Trends in Underlying Inflation
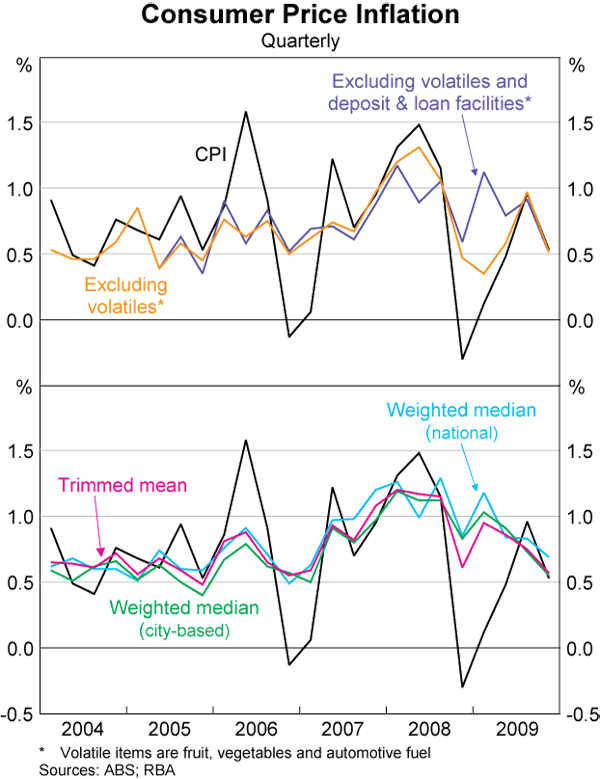
Quarterly movements in the headline CPI and some of the underlying measures discussed above are shown in Graph 2. The broadly similar movements depicted by the various measures of underlying inflation are reflected in the relatively high correlation coefficients between these series (Table 1). While there are typically some modest differences between the underlying estimates, all these series are significantly smoother than the headline CPI measure. In recent years, there have been a number of notable examples where the underlying measures have abstracted from large changes in particular prices that had a significant effect on the headline series. In June 2006, for example, CPI inflation was 1.6 per cent in the quarter, around twice the rate of inflation suggested by various underlying measures because of large movements in banana and automotive fuel prices. More recently, large falls in automotive fuel prices and the estimated price of D&L facilities resulted in very low quarterly outcomes for CPI inflation in the December quarter of 2008 and the March quarter of 2009.
| Trimmed mean | Weighted median (national) | Exclusion (volatile) | Exclusion (volatiles and D&L) | Trimmed mean (city) | Weighted median (city) | Headline CPI | |
|---|---|---|---|---|---|---|---|
| Trimmed mean | 1.00 | 0.89 | 0.68 | 0.70 | 0.98 | 0.93 | 0.57 |
| Weighted median (national) |
0.89 | 1.00 | 0.45 | 0.58 | 0.85 | 0.90 | 0.40 |
| Exclusion (volatiles) | 0.68 | 0.45 | 1.00 | 0.76 | 0.73 | 0.56 | 0.65 |
| Exclusion (volatiles and D&L) | 0.70 | 0.58 | 0.76 | 1.00 | 0.70 | 0.65 | 0.39 |
| Trimmed mean (city-based) |
0.98 | 0.85 | 0.73 | 0.70 | 1.00 | 0.91 | 0.65 |
| Weighted median (city-based) |
0.93 | 0.90 | 0.56 | 0.65 | 0.91 | 1.00 | 0.42 |
| Headline CPI | 0.57 | 0.40 | 0.65 | 0.39 | 0.65 | 0.42 | 1.00 |
|
Sources: ABS; RBA |
|||||||
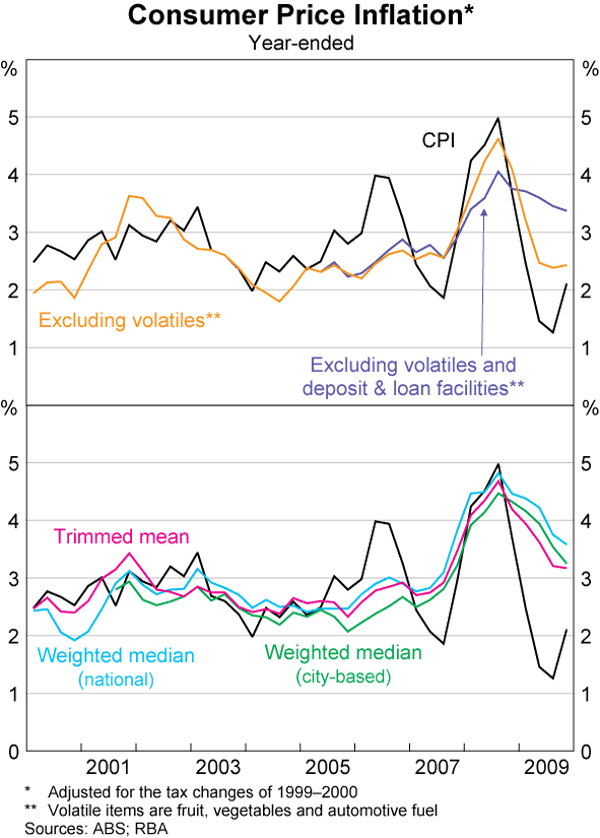
The various estimates all suggest a decline in underlying inflation through 2009, following the easing in demand pressures in the economy in 2008. The moderation in inflation is also apparent in measures of year-ended underlying inflation (Graph 3). Again, there are some divergences, but looking across the measures, year-ended underlying inflation peaked at a little over 4½ per cent over the year to the September quarter 2008 and has fallen to around 3¼ per cent over 2009. This moderation is expected to continue into 2010, with year-ended underlying inflation forecast to be around or slightly below 2½ per cent in late 2010 and early 2011.
Use of Estimates of Underlying Inflation at the Reserve Bank
Estimates of underlying inflation are a useful tool for understanding recent inflation outcomes, which is the starting point in the forecasting process. Given that CPI inflation is quite volatile, most of the models and equations used in the Bank to explain inflation use some measure of underlying inflation (often 15 per cent trimmed-mean inflation) as the dependent variable. So forecasts of inflation typically start with forecasts of underlying inflation, which then feed into the forecast for CPI inflation. In addition, an understanding of the current pace of inflation is an important judgmental input into any forecast for inflation. Measures of underlying inflation are one of the tools used by Bank staff in considering what part of recent price movements is likely to be ‘noise’ and what is likely to be persistent and to therefore have implications for future inflation.
As noted above, there is usually some divergence between different estimates of underlying inflation. Reflecting this, it is unlikely that any single measure of underlying inflation, or any simple formula based on the available measures, can be held up as the best measure at all times, and the relative usefulness of different series may change depending on the nature of the price shocks. Accordingly, in addition to looking at a range of underlying measures, Bank staff also look closely at the movements in particular CPI components, at analytical sub-groups of components such as tradables and non-tradables, and at the broader economic forces influencing inflation at any point.
Footnotes
The authors are from Economic Analysis Department. [*]
This article draws on earlier work at the Bank, including RBA (2002, 2005); Roberts (2005); Richards (2006); and Brischetto and Richards (2007). [1]
Some other measures of underlying inflation involve more significant reweighting of the CPI, giving higher weights to items that are less volatile and might contain more information about the persistent or generalised component of inflation. A disadvantage of these is that the weights are typically based on the properties of the price series, rather than households' expenditure patterns, so they will not necessarily correspond closely to the general increase in the cost of living as measured by the CPI, the target variable. Other approaches to estimating underlying inflation use econometric modelling, proceeding from various prior beliefs or restrictions about the relationship between inflation and other variables, although this type of approach is not widely used, at least in central banks' external communications. Finally, there are approaches, including those of Gillitzer and Simon (2006) and Hall and Jääskelä (2009), that employ some form of time-series smoothing. [2]
Items are ‘down-weighted’ in the sense that even when an item is trimmed and ‘excluded’ it still affects the trimmed mean. In particular, the fact that an item has been trimmed in any period means that some other item that experienced a relatively high or low price change will not be trimmed. Trimmed-mean measures are accordingly sometimes referred to as limited-influence estimators. [3]
See Wilcox (2005) for further discussion of how trimmed means can be better estimators of the central part of the distribution than conventional sample means, in particular how they are more robust in cases of non-normal distributions. [4]
The US weighted-median inflation rate calculated by the Federal Reserve Bank of Cleveland now incorporates this methodological improvement (see Bryan and Meyer 2007). [5]
The largest single item in the Australian CPI is house purchase costs, with an effective weight of 8 per cent. [6]
The bars in the graph sum to a little less than 100 per cent because a small proportion of items in the CPI had price changes outside the scale of the graph. [7]
These estimates are based on the December quarter 2009 CPI data, seasonally adjusted at the component level, where appropriate. As with all seasonally adjusted series – including estimates of seasonally adjusted headline CPI inflation – they are subject to some modest revision as seasonal factors are re-estimated. Experience has shown that revisions to trimmed-mean inflation tend to be very small. While weighted-median inflation is more subject to revision, revisions to the city-based estimates are likely to be smaller than for the estimates based on national data. [8]
This is also the practice for the trimmed-mean measures published by the Federal Reserve Banks of Cleveland and Dallas and the Bank of Japan. The practice in Canada, New Zealand and Switzerland has been to use the annual distribution of price changes. [9]
References
Brischetto A and A Richards (2007), ‘The Performance of Trimmed Mean Measures of Underlying Inflation’, Paper presented at the Conference on Price Measurement for Monetary Policy sponsored by the Federal Reserve Banks of Cleveland and Dallas, Dallas, 24–25 May (an updated version of RBA Research Discussion Paper No 2006-10).
Bryan MF and BH Meyer (2007), ‘Methodological Adjustments to the Median and 16 Percent Trimmed-Mean CPI Estimators’, Federal Reserve Bank of Cleveland, September.
Gillitzer C and J Simon (2006), ‘Component-Smoothed Inflation: Estimating the Persistent Component of Inflation in Real Time’, RBA Research Discussion Paper No 2006-11.
Hall J and J Jäääskelä (2009), ‘Inflation Volatility and Forecast Accuracy’, RBA Research Discussion Paper No 2009-06.
RBA (2002), ‘Box D: Underlying Inflation’, Statement on Monetary Policy, May, pp 55–56.
RBA (2005), ‘Box D: Measures of Underlying Inflation’, Statement on Monetary Policy, August, pp 65–66.
Richards A (2006), ‘Measuring Underlying Inflation’, RBA Bulletin, December, pp 9–18.
Roberts I (2005), ‘Underlying Inflation: Concepts, Measurement and Performance’, RBA Research Discussion Paper No 2005-05.
Wilcox RR (2005), Introduction to Robust Estimation and Hypothesis Testing, 2nd edn, Elsevier Academic Press, Amsterdam.