Bulletin – November 2001 Measuring the Real Exchange Rate^[1]

Introduction

The real exchange rate is an important concept in economics. It is a broad summary measure of the prices of one country's goods and services relative to those of another country or group of countries, and is thus an important consideration when analysing macroeconomic conditions in open economies.

In theory, calculating a real exchange rate is relatively straightforward – it depends on the nominal exchange rate and relative price levels. In practice, however, when calculating or measuring the real exchange rate a large number of choices have to be made. These include: how many countries are to be compared, which domestic price measures are the most appropriate, how are the movements in the different bilateral real exchange rates to be aggregated, and what weights are to be used? These and some related issues are discussed in this article. Several exchange rate indices that have been used in analytical work at the RBA are also presented; henceforth, some of these will be updated quarterly and published in the statistics section of the RBA website <www.rba.gov.au/statistics/>.

Defining the Real Exchange Rate

As mentioned above, a real exchange rate between two countries is calculated as the product of the nominal exchange rate and relative price levels in each country. The real exchange rate between foreign country i and the home country at time t is thus:

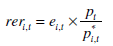(1)

where p is the price level of the home country, p^*_i is the price level in foreign country i, and e_i is the nominal exchange rate between the currencies of foreign country i and the home country, expressed as the number of foreign currency units per home currency unit so that e_i rises with an appreciation of the home-country currency.^[2]

To convert a set of bilateral indices into a multilateral real exchange rate index, a weighted average of the bilateral indices (rer_i,t) needs to be taken. While an arithmetic weighted average of these indices is straightforward to calculate, there are statistical reasons to prefer a geometric average of the indices. In particular, in contrast to an arithmetic average, a geometric average treats increases and decreases in exchange rates symmetrically and is not affected by the choice of base year. The weighted average of the real bilateral exchange rates is thus generally calculated as:

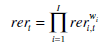(2)

where the weights, w_i, which are applied to each bilateral real exchange rate, sum to one.

In the above formulation, the weights used to construct the real exchange rate index are held constant over time. It may, however, be desirable to allow the weights to change periodically, in order to ensure that movements in the real exchange rate provide a meaningful picture of the net effect of movements in bilateral rates at different times. If the weights are allowed to vary, the index must be spliced together at every period that the weights are changed. Otherwise, movements in the index would be misleading, as they would reflect both changes in the underlying real bilateral exchange rates as well as changes in the weights over time.

There are several conceptually correct methods for calculating an index with changing weights. One that is commonly used can be characterised as a spliced Laspeyres index. Without going into the details, suppose that the weights applied to each bilateral real exchange rate change from w¹ i to w² i at time B. Then for t ≥ B, the spliced real exchange rate index is given by:

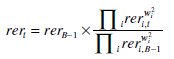(3)

If the composition of countries in the basket has changed for the new set of weights, the set of bilateral exchange rates used for both parts of the second term in this expression are those included in the current-period set of weights.

Practical Calculation Issues

In practice, when calculating a real exchange rate index for analytical purposes, there are a number of issues that then have to be considered. In most cases the choices made will depend on the purpose for which the real exchange rate is being constructed. Some of these issues and the main alternatives are briefly raised below.

Which bilateral rates should be included?

In general, it is desirable to include all currencies in a real exchange rate index which have ‘significant’ weights. For example, in constructing the nominal trade-weighted index of the Australian dollar, the Reserve Bank includes enough countries to account for at least 90 per cent of Australia's total international merchandise trade. However, large exchange rate movements specific to a single currency may sometimes result in the index giving a misleading indication of overall changes in competitiveness. It may then be appropriate to exclude some currencies from the index calculations for some purposes. Following the Asian crisis, this was the case for some of the east Asian currencies which had depreciated sharply in 1997 and 1998.

Which price measure should be chosen?

The most commonly used price series used in constructing real exchange rates are consumer price indices (CPIs). These have the advantage of being timely, similarly constructed across countries and available for a wide range of countries over a long time span. In some cases, it is preferable to use ‘core’ or underlying measures of the CPI, to abstract from the volatility introduced by food and energy prices, but making this adjustment should have relatively little effect on medium-term real exchange rate developments. Adjusting for the effect that changes in indirect tax rates have on the CPI is also desirable.

Alternative price indices that are sometimes used include producer price indices or a measure of business costs, such as unit labour costs. These are arguably preferable if real exchange rates are intended to capture movements in competitiveness, although they are often difficult to obtain on a comparable basis across more than a few countries over a reasonable length of time.

Which weights should be chosen?

The choice of weighting scheme depends crucially on the purpose for which the real exchange rate is being constructed. For assessing changes in competitiveness, for example, the relative importance of a nation's trading partners seems an obvious choice of weights. Weights calculated as the share of total trade (exports plus imports) with each trading partner are used by the RBA in calculating the trade-weighted index. Alternative, trade-based weighting schemes can be based on either bilateral export or import shares.

For some purposes, however, these weighting scheme may be less than ideal, as they capture only the bilateral trade between the home country and its trading partners, which may not be a good proxy for the importance of these countries in determining world price and demand conditions. Alternative approaches are to construct weights that better capture the changes in the home country's competitiveness relative to competing suppliers of its exports using third-country export weights or shares in world trade. The approach adopted by the IMF in constructing its Multilateral Exchange Rate Model (MERM) exchange rate indices, is to construct weights using a general equilibrium model of world trade, which is designed to incorporate the estimated responses of trade patterns to movements in exchange rates.

Even these indices, however, are restricted to basing their weights on only goods and services that are actually traded. This does not necessarily correspond to countries' shares of world production, and hence their influence on world markets. For this reason, it is sometimes preferable to use weights based on countries' shares of world GDP, although this raises additional complications, as it is not straightforward to convert different countries' GDPs to a common currency in order to calculate these weights.

All of the weighting schemes discussed above focus on countries' trading behaviour. For some purposes, however, it may be preferable to use weights based on characteristics of countries' capital markets such as their international investment positions. This then raises a host of additional issues that need to be considered, such as the treatment of assets and liabilities denominated in domestic currency.^[3]

Some Alternative Real Exchange Rates

Graphs 1 and 2 show a set of quarterly nominal and real exchange rate indices. The data for the real trade-weighted, import-weighted, export-weighted and G7 GDP-weighted indices are available on the Bank's website (on the statistics page) and will be updated quarterly. Data sources for these series are detailed in the research paper (RDP 2001-04).

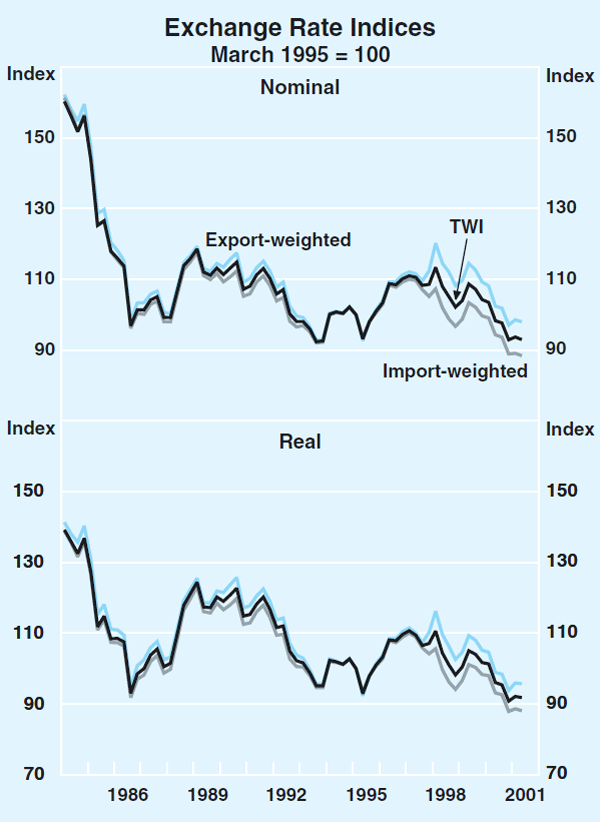
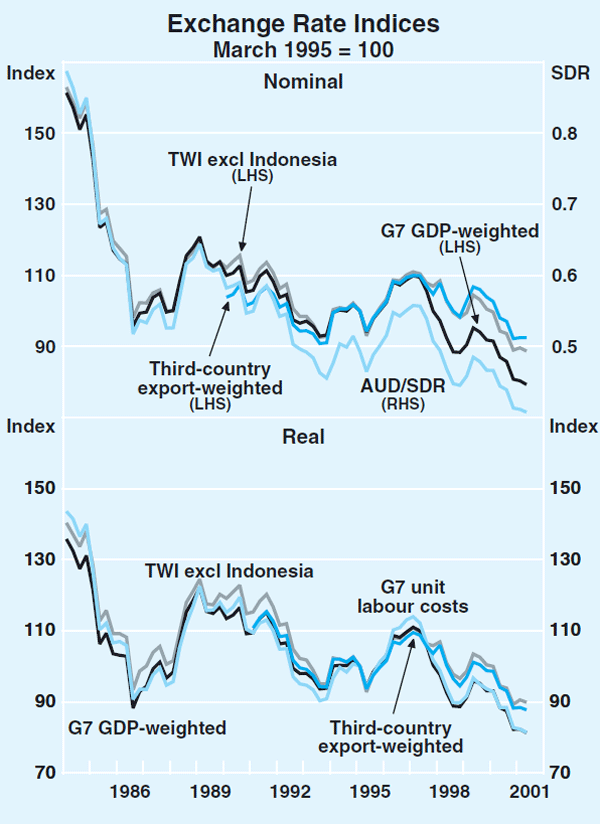
All but one of the series presented in Graphs 1 and 2 are calculated using country CPIs (core where available) as the price indices. In Australia's case the underlying CPI has also been adjusted for the recent change in indirect taxation arrangements. The only differences between the series presented in these graphs are thus country coverage and weighting schemes, and the use of unit labour costs instead of CPIs for one series.

It is apparent from these graphs that all of these alternative real exchange rate indices move broadly similarly, although there are, on occasions, some significant divergences. In a few cases, and over short horizons, the different series do not agree on the direction of exchange rate movements. Over somewhat longer horizons, the series can sometimes differ quite significantly in their assessments of the magnitudes of movements in competitiveness. This is particularly the case when the home currency is appreciating against some currencies and depreciating against others, as occurred for Australia in 1997 and 1998, and for the major industrialised countries on several occasions.

Further analysis presented in the research paper also demonstrates that the choice of real exchange rate can affect assessments of the fundamental determinants of the real exchange rate, as well as assessments of the effect of the exchange rate on other variables in the economy.

Conclusion

This article sets out some issues that must be confronted when constructing real exchange rate indices for analytical work. It argues that there is no single measure of the real exchange rate that that is ideal for all purposes. In many cases the appropriate choice depends on the particular issue being addressed, and this will determine the most appropriate weighting scheme, price deflators, index number formulae and country coverage. In some cases data availability and quality will affect the ultimate choice of the researcher. The article has, however, set out some basic issues for which there is a generally preferred approach. Some of these are algebraic considerations: geometric averages are preferable to arithmetic averages. Other issues relate to index number theory: if the quantities underlying the weights used in the index's construction are moving, it makes sense to allow the weights to change. If the weights change, however, it is essential that the index be carefully spliced together.

Footnotes

This article was prepared by Luci Ellis, Economic Research Department. It summarises the results of research work that this author has published in RBA Research Discussion Paper No 2001-04, entitled ‘Measuring the Real Exchange Rate: Pitfalls and Practicalities’. Staff research published by the Bank is intended to contribute to debate and does not necessarily reflect the views of the Bank. [1]

Some literature uses the alternative presentation of the exchange rate as the number of home currency units per foreign currency units, where an appreciation is recorded as a fall in the index. It should be noted that standard market quotations for currencies may be in either format. For the Pound sterling, New Zealand dollar, Australian dollar, PNG kina, the euro and the currencies of most Pacific nations, market quotations are generally for number of US dollars per home currency unit (denoted, for example, AUD/USD). For all other currencies, the quotation is usually in the form of home currency units per US dollar (e.g. USD/JPY). [2]

These issues are discussed in considerable detail in RDP No 2001-04. [3]