RDP 2008-04: A Small BVAR-DSGE Model for Forecasting the Australian Economy 4. Results – Estimation
September 2008
4.1 DSGE
Table 2 presents the mean of the posterior distributions of the DSGE parameters; the posterior densities are shown in Figure C1 in Appendix C.[13],[14]
Examples of parameters where the data shift the posterior distribution away from the prior include the intertemporal elasticity of substitution (τ), for which we find a posterior mean of 0.5. This indicates that consumers are less willing than expected to change their consumption decisions in response to interest rate shocks. For the persistence of technology shocks (pz), we find a posterior mean of 0.29, which is broadly similar to the 0.4 estimate of Lubik and Schorfheide (2007).
We obtain 0.8 as our posterior mean for the nominal interest rate smoothing parameter ρR, which is comparable to the estimates from other recent DSGE studies, such as the posterior mode of 0.87 obtained by Nimark (2007). Our posterior mean estimates of ψ1 and ψ2 suggest that monetary policy responds more aggressively to deviations of inflation from steady state than output, consistent with Nimark.
Also interesting is that we find that the posterior mean of the persistence of foreign
inflation (ρπ*) is lower than expected and that the posterior
mean of the standard deviation of foreign inflation shocks 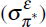 is considerably larger
than expected. This reflects the fact that the foreign inflation shock
is considerably larger
than expected. This reflects the fact that the foreign inflation shock 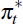 captures deviations from the rather strict assumption of PPP (a point noted by Lubik
and Schorfheide 2007).
captures deviations from the rather strict assumption of PPP (a point noted by Lubik
and Schorfheide 2007).
| Parameter | Prior mean | Posterior mean | 90 per cent interval |
|---|---|---|---|
| Households and firms | |||
| τ | 0.6 | 0.50 | [0.36, 0.66] |
| α | 0.2 | 0.20 | [0.18, 0.21] |
| rss | 2.5 | 2.48 | [1.66, 3.26] |
| Phillips curve | |||
| κ | 0.3 | 0.42 | [0.28, 0.58] |
| Taylor rule | |||
| ρR | 0.77 | 0.81 | [0.75, 0.87] |
| Ψ1 | 1.6 | 1.62 | [1.31, 1.94] |
| Ψ2 | 0.4 | 0.40 | [0.07, 0.67] |
| Exogenous persistence | |||
| ρΔq | 0.4 | 0.57 | [0.49, 0.65] |
| ρπ* | 0.8 | 0.53 | [0.36, 0.70] |
| ρy* | 0.9 | 0.92 | [0.86, 0.98] |
| ρz | 0.5 | 0.29 | [0.05, 0.74] |
| Exogenous shock standard deviations | |||
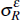 |
0.1 | 0.08 | [0.06, 0.10] |
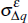 |
1.9 | 1.23 | [1.01, 1.43] |
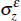 |
0.2 | 0.35 | [0.10, 0.47] |
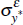 |
0.5 | 0.54 | [0.25, 0.82] |
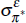 |
0.15 | 2.91 | [2.33, 3.50] |
4.2 Selection of λ and Lag Length
We consider lag lengths of 2, 3 and 4 for the VAR component of the BVAR-DSGE. To determine the relative weight on the DSGE model, we let the set of possible λ be Λ = [0.75,1,1.25,1.5,1.75,2,5,10,100,000].[15] Using the marginal data density measure of Equation (2), which focuses on in-sample fit, we find the best combination to be a VAR(3) with λ = 1.[16] This implies that we place equal weight on the DSGE model and the VAR, which was also found for New Zealand by Lees et al (2007). Alternatively, a lower weighting of 0.6 was used by Del Negro and Schorfheide (2004).
To select λ with reference to the out-of-sample forecasting performance, we estimate BVAR-DSGE models corresponding to each possible value of λ over the grid Λ, at each lag length. We truncate the sample to end in 2001:Q4, estimate the model, construct the forecasts, advance the end-date by one quarter and repeat the process, until the last end-date of 2007:Q3. To construct the forecasts we first draw a matrix of VAR parameters Φ and a variance-covariance matrix Σu from their posterior distributions. Given Σu we draw a vector of innovations ut+1 from the multivariate-normal distribution N(0,Σu), and compute yt+1 using the VAR with parameters Φ. Further draws of innovations enable us to compute the sequence of forecasts yt+2, yt+3, ..., yt+h using previous forecasts for the lags in the VAR (that is, the forecasts are dynamic). By repeating this entire process 1,000 times we construct a distribution of forecasts, which we summarise by calculating the mean forecast at each horizon. As we do this for each estimation end-date, we obtain a sequence of forecasts for each horizon; for example, we construct 24 one-quarter-ahead forecasts (the last being those made in 2007:Q3 for 2007:Q4) and 17 eight-quarter-ahead forecasts. We then evaluate the forecasts by calculating the Root-Mean-Squared Error (RMSE).
In the results that follow, we focus on the models' ability to forecast output growth, inflation and interest rates. These are the key policy variables, and the other variables are difficult to forecast (particularly the exchange rate; see Meese and Rogoff 1983).
Table 3 presents the RMSE of the forecasts for each variable one quarter ahead, and for their year-ended changes four and eight quarters ahead, except for interest rates, where we report its value at these horizons. These forecasts are computed for different values of λ in the manner just described, using a VAR with three lags. It suggests that by moderately increasing the weight on the DSGE prior from that recommended by the marginal data density – to between 1.5 and 2 – we generally improve the model's forecasting performance, particularly for output growth and inflation one quarter ahead. Placing an even larger weight on the prior further improves the year-ahead interest rate forecasts, but at the expense of some deterioration in the near-term growth and interest rate forecasts.
| λ | One quarter ahead | Four quarters ahead | Eight quarters ahead |
|---|---|---|---|
| Quarterly | Year-ended | Year-ended | |
| Output | |||
| 0.75 | 0.338 | 0.629 | 0.742 |
| 1 | 0.333 | 0.622 | 0.756 |
| 1.25 | 0.329 | 0.618 | 0.766 |
| 1.5 | 0.326 | 0.614 | 0.796 |
| 1.75 | 0.326 | 0.613 | 0.789 |
| 2 | 0.324 | 0.609 | 0.801 |
| 5 | 0.337 | 0.588 | 0.812 |
| 10 | 0.354 | 0.607 | 0.779 |
| Interest rates | |||
| 0.75 | 0.201 | 0.709 | 0.713 |
| 1 | 0.197 | 0.665 | 0.687 |
| 1.25 | 0.195 | 0.631 | 0.662 |
| 1.5 | 0.196 | 0.585 | 0.624 |
| 1.75 | 0.196 | 0.581 | 0.619 |
| 2 | 0.196 | 0.560 | 0.603 |
| 5 | 0.210 | 0.472 | 0.519 |
| 10 | 0.216 | 0.439 | 0.502 |
| Inflation | |||
| 0.75 | 0.167 | 0.332 | 0.341 |
| 1 | 0.163 | 0.335 | 0.337 |
| 1.25 | 0.160 | 0.337 | 0.330 |
| 1.5 | 0.155 | 0.344 | 0.339 |
| 1.75 | 0.156 | 0.345 | 0.324 |
| 2 | 0.150 | 0.339 | 0.328 |
| 5 | 0.150 | 0.373 | 0.350 |
| 10 | 0.149 | 0.383 | 0.365 |
| Note: The interest rate forecasts are for its level at all horizons. | |||
It is also possible to compare the forecasting performance at different lag lengths for the VAR (Table E1 in Appendix E). In general, the interest rate forecasts are most accurate when only two lags are used, whereas for the other variables the one-year-ahead forecasts are improved by using three lags. We place a greater weight on the accuracy of the inflation and output forecasts relative to those for interest rates, and consequently the BVAR-DSGE results in the remainder of this paper are computed with a VAR(3) and λ = 1.75.[17]
Footnotes
We construct the posteriors using the Metropolis-Hastings algorithm with a Markov chain 500,000 observations long. To ensure convergence we drop the first 250,000 simulations and simulate a second chain for comparison. All estimation was conducted using Dynare 4, in Matlab R2007b and R2008a. Dynare is developed by S Adjemian, M Juillard and O Kamenik; see <http://www.cepremap.cnrs.fr/juillard/mambo/index.php> for further information. We manage Dynare 4 with TortoiseSVN, available from <http://tortoisesvn.net/>. [13]
These posterior densities depend on λ via the marginal likelihood, P(Y|θ) (see Equation (A.2) in Del Negro and Schorfheide (2004)). They are for λ = 1.75, which is selected in Section 4.2. [14]
Placing a large weight on λ is akin to estimating the DSGE model. The unrestricted VAR we estimate separately in Section 5.1 is effectively λ = 0, since it places zero weight on the DSGE model. [15]
The means of the posterior distributions of the DSGE parameters when λ = 1 are similar to those presented in Table 2. [16]
Ideally, the latter results would be constructed over a separate sample than that used to select λ. However, as we wished to only use the inflation-targeting period, this was impractical. [17]