RBA Annual Conference – 1997 The Smoothing of Official Interest Rates Philip Lowe and Luci Ellis[*]
1. Introduction
Central banks tend to move official interest rates in a sequence of relatively small steps in the same direction, a practice known as interest-rate smoothing. This paper documents this practice, examines its implications and discusses reasons why central banks move interest rates in this way.
The practice of interest-rate smoothing is evident in many countries. In the most recent interest-rate cycle in Australia, the target cash rate was increased three times in 1994 and has been reduced four times in 1996 and 1997. Similarly, in the United States, the federal funds target rate was increased seven times in 1994 and 1995, and then reduced three times in 1995 and 1996. The fact that official interest rates are moved multiple times in the same direction leads to a clear cycle in interest rates. Some commentators have argued that this interest-rate cycle contributes to, rather than ameliorates, the business cycle. By implication, the argument is that if interest rates exhibited a less cyclical pattern, with central banks being prepared to move rates in large steps and more decisively, the amplitude of the business cycle could be reduced.
In contrast, the central argument of this paper is that some degree of interest-rate smoothing represents optimal behaviour on the part of central banks. The lags between a change in monetary policy and its effect on economic activity, and the fact that the economy is subject to shocks from many sources, mean that frequent changes in the level and direction of interest rates are unlikely to reduce substantially the variability of inflation and output. Furthermore, frequent directional changes in the level of official interest rates risk rendering ineffectual the ‘announcement’ effects of monetary policy, increasing instability in financial markets and reducing the credibility and accountability of the monetary authorities. None of these developments would be expected to contribute to the stability of either output or inflation.
The paper itself is structured as follows. Section 2 examines common features across countries in the pattern of changes in official interest rates. Section 3 briefly reviews the existing literature on the causes and effects of interest-rate smoothing. Sections 4 and 5 then examine the proposition that interest-rate smoothing is responsible for the business cycle and represents suboptimal behaviour. In the first of these sections, we use a simple linear model of the Australian economy to examine the implications for the dynamics of output, inflation and interest rates of a constraint which imposes a cost when interest rates are changed. In the following section we go beyond this linear model and discuss reasons why changes in interest rates might have some non-linear effect on the variables of concern to the monetary authorities. These non-linear effects add to the arguments for smoothing official interest rates. Finally, Section 6 draws together the main conclusions of the paper.
2. Common Patterns in Official Interest Rates
While there are differences in the pattern of changes in official interest rates across countries, there are also a number of important similarities. These similarities are most pronounced amongst countries which are explicit about using an interest rate as the operating mechanism for monetary policy. In these countries, as well as in many others, central banks smooth changes in official interest rates. This involves:
- changing official interest rates relatively infrequently;
- changing official interest rates in a sequence of steps in the same direction; and
- leaving official interest rates unchanged for a relatively long time before moving in the opposite direction.
These characteristics can be seen in Table 1 which presents statistics on the frequency, and number, of changes in official interest rates over the period since July 1985 for Australia, the United States, the United Kingdom, Japan and Germany. Figure 1 shows the levels of the various interest rates.
| Country | Official policy rate |
Sample period | Number of business days between change in policy rates |
Ratio of continuations to reversals | Absolute size of changes (average basis points) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All changes | Reversals | Continuations | All changes | Reversals | Continuations | |||||||
| Mean | Median | Mean | Median | Mean | Median | |||||||
| Australia | Cash rate target |
7/85–5/97 1/92–5/97 |
74 121 |
52 78 |
144 349 |
98 349 |
54 75 |
46 59 |
3.3 5.0 |
108 71 |
142 63 |
99 73 |
| United States | Federal funds target rate |
7/85–5/97 1/92–5/97 |
38 98 |
20 63 |
87 260 |
34 299 |
28 54 |
19 56 |
5.3 3.7 |
24 36 |
21 25 |
24 39 |
| United Kingdom | Base lending rate |
7/85–5/97 1/92–5/97 |
57 92 |
34 63 |
102 161 |
100 154 |
43 77 |
26 55 |
3.2 4.3 |
59 52 |
65 33 |
57 56 |
| Japan | Discount rate | 7/85–5/97 1/92–5/97 |
139 161 |
97 122 |
405 – |
405 – |
106 161 |
89 122 |
8.5 – |
61 67 |
63 – |
60 67 |
| Germany | 14-day repo rate |
7/85–5/97 1/92–5/97 |
14 14 |
5 5 |
14 20 |
6 15 |
14 14 |
5 5 |
2.0 11.3 |
12 8 |
13 12 |
11 8 |
| Discount rate | 7/85–5/97 1/92–5/97 |
103 75 |
85 51 |
96 42 |
96 42 |
104 78 |
85 65 |
8.3 14.0 |
52 47 |
50 50 |
52 46 |
|
| Notes: (a) Prior to January 1990, the Reserve Bank of Australia did not
announce its target for the cash rate. The observations on the target cash
rate prior to this time are derived from internal documents, including
the informal trading ranges that guided the Bank's domestic-market
operations. (b) Interest-rate data for the United States, United Kingdom, Japan and Germany were obtained from Datastream. (c) Prior to February 1987 the 28-day repo rate (rather than the 14-day repo rate) is used for Germany. |
||||||||||||
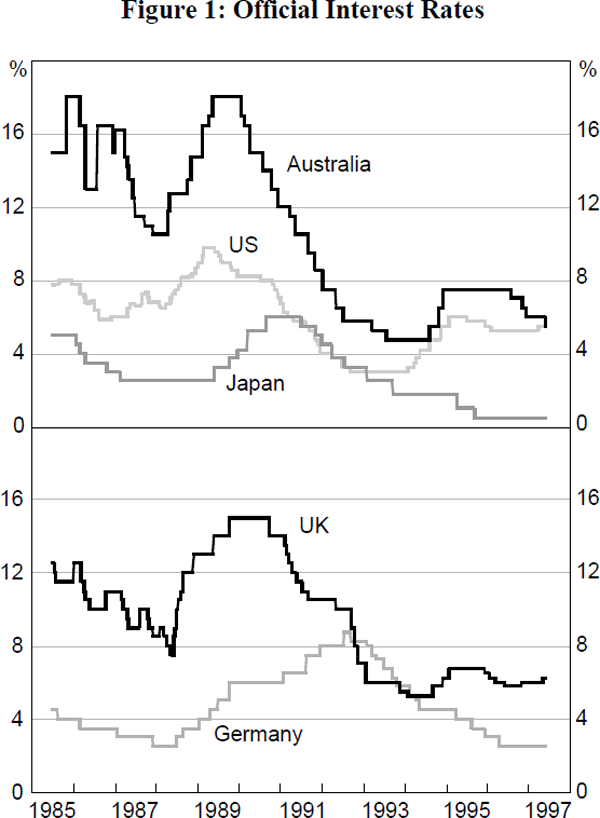
The first characteristic is that changes in official interest rates are relatively rare given the frequency with which information about the state of the economy and inflation is released. Almost every day some new piece of information becomes available. While, in general, this should not lead to large day-to-day changes in the central bank's forecasts of inflation and activity, these forecasts should change (at least at the margin) each time information is released. This would suggest that frequent changes in interest rates should be observed. In practice, most central banks adjust interest rates less frequently than once a month and often go several quarters without a change in rates. For example, since July 1985, the Reserve Bank of Australia's target cash rate has been adjusted, on average, once every 3½ months (74 business days), with 18 months being the longest period without a change. More frequent changes have occurred in the base lending rate in the United Kingdom, while the federal funds target rate has, on average, been adjusted once every eight weeks. Of the five countries for which data are presented in Table 1, German interest rates have been moved most frequently, with the average time between changes in the repo rate being around three weeks; the discount rate, however, has been changed much less frequently.
Further, there is some evidence that the frequency of interest-rate changes has declined over recent years (Table 1 and Figure 1); this seems to be particularly the case in the United States. Whether or not this represents a permanent change is difficult to judge as the frequency of interest-rate changes is a function not only of operating procedures but also of the shocks that are hitting the economy. However, a possible reason is that the move towards explicit announcement and explanation of policy changes has had some effect on the pattern of changes in official interest rates. This issue will be discussed in more detail later in the paper.
When official interest rates are actually changed, the changes are generally made in multiples of a quarter of a percentage point. In the United States, the most common size of move over the past decade has been a quarter of a percentage point, with the largest move being three-quarters of a percentage point. In Australia, moves have tended to be larger (and correspondingly the amplitude of the interest-rate cycle larger) with the most frequent size of move being one percentage point, although the four most recent moves have each been half this size. Half of a percentage point has also been the most common size of change in the base lending rate in the United Kingdom and the discount rate in Germany.
The second characteristic of interest-rate smoothing is that changes in the direction of interest rates are relatively rare. Central banks appear to have a strong preference for implementing a sequence of interest-rate changes in the same direction. It is not unusual for three or four moves to be made in the same direction before a move is made in the opposite direction. This pattern means that changes in policy interest rates are autocorrelated, and as a result, partly predictable. This can be seen in the autocorrelation coefficients shown in Table 2. In all five countries, quarterly changes in official interest rates are positively autocorrelated; if an increase in interest rates is observed this quarter, on average, an increase will occur in the following quarter. Over the period from July 1985, the first autocorrelation is significant for all countries except for Australia. The low value for Australia reflects the volatility in the target cash rate during 1985 and 1986 when the exchange rate was under significant downward pressure; if we start the sample period at the beginning of 1987, the first autocorrelation is similar in magnitude to that for the United States and is highly significant.
| Lags (in quarters) | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 6 | 8 | 10 | 12 | |
| Australia | 0.07 | 0.12 | 0.18 | −0.02 | −0.21 | −0.32* | −0.08 | −0.09 |
| United States | 0.51* | 0.22 | 0.19 | 0.06 | 0.10 | −0.12 | −0.45* | −0.17 |
| United Kingdom | 0.35* | 0.11 | 0.20 | 0.07 | 0.07 | −0.14 | −0.26 | −0.22 |
| Japan | 0.30* | 0.35* | 0.39* | 0.05 | −0.05 | −0.09 | −0.32 | −0.31 |
| Germany | 0.34* | 0.42* | 0.41* | 0.17 | 0.03 | −0.06 | −0.04 | −0.02 |
| Notes: (a) An asterisk (*) denotes significantly different from zero at
the 10 per cent level. (b) For Australia the first autocorrelation is 0.51, and significantly different from zero, if the sample period commences in 1987:Q1. (c) For Germany the discount rate is used. (d) End-of-quarter observations are used to calculate autocorrelations. |
||||||||
The positive autocorrelations extend to an horizon of three quarters in all countries, although the correlations are generally insignificant. By the time eight quarters is reached, the autocorrelations are negative, implying that if one observes an increase in interest rates in the current quarter, it is more likely than not that there will be a decline in rates in two years' time. The negative autocorrelations at these long horizons are largest for Australia and the United States.
Just as the frequency of interest-rate changes appears to have declined in recent years, the frequency of directional changes also appears to have declined. Again this is partly attributable to the changes in operating procedures and the monetary-policy framework as well as the nature of the shocks. In the mid 1980s, considerable instability in foreign-exchange markets translated into variability in official interest rates in the United Kingdom and Australia. It may be that as the focus of monetary policy has shifted towards medium-term inflation targets, the need for official interest rates to react to exchange-rate changes has declined, and as a consequence, official interest rates show a smoother pattern. Notwithstanding this, a period of considerable exchange-rate instability would probably lead to more frequent directional changes in interest rates than seen over recent years.
The third feature of interest-rate smoothing is that when reversals in the direction of official interest rates do occur they are generally preceded by a relatively long period without a change in rates. In all five countries examined, the average time between interest-rate changes is greater for reversals than it is for continuations. Typically, central banks have left interest rates unchanged for at least three months before they have reversed the previous move.
3. The Literature on Interest-rate Smoothing
The literature on interest-rate smoothing has two broad strands. The older strand centres around the issue of whether a central bank should target a monetary aggregate or an interest rate. In this literature, a central bank that adjusts the money supply to accommodate a shock to money demand is said to be smoothing interest rates, for in the absence of such an adjustment, interest rates would have changed. The most widely documented example of this type of smoothing is the elimination of the cycle in interest rates that arose out of the seasonal pattern of tax collections (Mankiw and Miron 1991).
There is also a related literature which describes interest-rate smoothing as the practice of setting the interest rate so that the best forecast of the future interest rate is the current rate. Such a practice has been described as smoothing since a constant expected interest rate means a smooth ex ante interest-rate profile. Of course, ex post the interest rate will not exhibit such a profile as shocks will cause the rate to change. Under this older definition of smoothing, interest-rate changes are uncorrelated with the interest rate being a random walk. Mankiw (1987) and Barro (1989) have argued that such an outcome is appropriate on the grounds that it smooths the inflation tax. Their argument is that changes in the inflation tax should not be predictable, so that changes in the nominal interest rate should not be predictable. The task for the monetary authorities is simply to move the nominal interest rate in line with the random changes in the real interest rate. While earlier work found some evidence that official interest rates could be described as random walks, this evidence stands in stark contrast to the empirical regularity of autocorrelated changes in official interest rates discussed in the previous section.
The second and more recent strand of literature on interest-rate smoothing takes it as given that the central bank targets an interest rate and that the rate is changed in pursuit of macroeconomic objectives. It then notes that the target interest rate tends to adjust slowly, and in a relatively smooth pattern (as discussed above). It is this more recent concept of interest-rate smoothing that is of interest here.
This type of smoothing is often captured in models by some form of partial-adjustment mechanism, with the central bank adjusting its target rate slowly towards the desired target rate (McCallum 1994a; Clarida and Gertler 1996). In other models, smoothing is captured by including a penalty for changing rates in the central bank's objective function, with the penalty increasing, at an increasing rate, in the size of the change (Debelle and Stevens 1995; Söderlind 1997).
Much of the recent literature on interest-rate smoothing has focused on the implications of the pattern of changes in official interest rates for tests of the term structure of interest rates.[1] McCallum (1994a) argues that the failure of standard empirical tests to support the expectations theory of the term structure arises from the tests not taking account of a monetary-policy reaction function which smooths interest rates and responds to the slope of the yield curve. Similar arguments have also been made by McCallum (1994b) to explain the failure of tests of uncovered interest parity, while Söderlind (1997) argues that the practice of interest-rate smoothing has implications for tests of the Fisher effect.
There are relatively few thorough treatments of why central banks actually engage in the practice of interest-rate smoothing. The explanations that have been discussed are generally based on the following hypotheses:
- that policy-makers dislike frequently reversing the direction of interest rates;
- that the nature of the decision-making process leads to conservatism; and
- that smooth changes in the target rate provide greater control over long-term interest rates and thereby greater control over inflation and economic activity.
A number of authors have attributed the practice to a desire by central banks to avoid large movements in financial-market prices. The argument is that by moving gradually and predictably, and minimising the frequency of directional changes, the central bank can reduce financial-market volatility. In doing so it reduces the possibility that the stability of the financial system is threatened by particular institutions incurring large losses.
Cukierman (1996) proposes a variant of the financial-stability argument. He notes that in the United States the average maturity of banks' assets is considerably greater than the average maturity of their liabilities. By reducing unpredictable volatility in official short-term interest rates (and thus volatility in the yield curve), the central bank can reduce the risks to the banking system that arise from the maturity mismatch. One difficulty with this argument is that smoothing appears just as prevalent in countries such as Australia, where the maturity mismatch is much smaller due to the predominance of variable-rate loans.
Caplin and Leahy (1997) suggest that policy-makers' dislike of frequent changes in the direction of interest rates arises not from a concern about financial stability, but rather from the perception that such changes make the policy-maker look poorly informed. The argument is that if a central bank lacks credibility, frequent turning points in interest rates could undermine confidence in the central bank. The authors conclude that as a central bank's reputation improves, the incentive to engage in smoothing declines. Again this conclusion appears not to be supported by the evidence, with even the most credible central banks smoothing interest-rate changes.
Explanations based on the decision-making process are emphasised by Chinn and Dooley (1997) and Goodhart (1996). The former imply that natural conservatism is at the heart of smoothing, while Goodhart argues that central banks cannot obtain broad-based political support for a change in interest rates until there is solid evidence that such a change in needed. That evidence only accumulates slowly, so that interest rates can only be changed slowly.
Another argument, advanced by Goodfriend (1991) and Roley and Sellon (1995), is that implementing a predictable path for short-term interest rates allows the central bank to exercise greater influence over long-term bond yields, and thus over future economic activity and inflation. In a similar vein, Poole (1991) argues that a good explanation for why central banks move in small steps is that it allows them to see how longer rates respond; if the rates do not respond sufficiently another move can be made.
While there is a variety of explanations, there is little, if any, published empirical work examining these hypotheses. On the whole, central banks also have had little to say on the pattern of interest-rate changes. One exception has been in the United States where Chairman Greenspan has been quoted as arguing that the current pattern of interest-rate changes contributes to the stability of the financial system. Further, Blinder (1995, p. 13), when vice-chairman of the Board of Governors, argued that ‘a little stodginess at the central bank is entirely appropriate’. In his Marshall lectures he proposed that central banks should calculate the change in policy required to ‘get it right’, then do less. Such a ‘rule’ appears to be motivated by the uncertainties that policy-makers face and, in particular, by the uncertainty that policy-makers have about the parameters of the underlying model (Brainard 1967).
The impact that interest-rate smoothing has on the economy has also received relatively little attention, although the idea that central banks move too little and too late is an old one. Recently this argument has been made by Goodhart (1996) who argues that the process of smoothing has contributed to the cycles in activity and inflation. A more subtle argument is made by Caplin and Leahy (1996). They argue that the practice of moving in small steps actually alters the reaction of the economy to changes in monetary policy. The idea is that individuals recognise the pattern of interest-rate changes employed by central banks, and that as a result, they react less to a change in policy than would otherwise be the case, waiting for further changes in the same direction. By implication, the protracted nature of recessions is a by-product of central bank behaviour. The authors conclude that, rather than adjusting policy gradually, ‘policy needs to be more aggressive than the reaction it seeks to elicit’ (p. 699).
The issues of why central banks smooth interest rates and the effect of the smoothing are taken up in the following sections.
4. The Impact of Interest-rate Smoothing in a Simple Model
Goodhart (1996) argues that the practice of smoothing leads central banks to respond too slowly to shocks, and that this slow response leads to unnecessary cycles in economic activity and inflation. Goodhart and Huang (1996) present a simple model in which a central bank with an inflation objective should deliver interest-rate changes which are uncorrelated, with the best guess of tomorrow's interest rate being equal to the (constant) equilibrium rate. In their model, such a policy would eliminate cycles in activity and inflation.
Cecchetti (1996) makes a similar point although he does not claim that larger movements in interest rates could eliminate the cycles in inflation and output. Rather, he argues that interest-rate changes in the United States are smoother than would be suggested by a policy that was attempting to minimise the variability of either inflation or nominal income. He concludes that this smoother pattern has increased inflation variability (although not output variability).
Comprehensive evaluation of these propositions is a difficult exercise. Goodhart's argument that cycles in inflation and activity could be eliminated by a central bank moving interest rates more aggressively is inevitably model-dependent. If one uses a model with a more complicated lag structure than that used by Goodhart, it is possible to show that serially correlated interest-rate changes can represent optimal policy, with such a policy leading to serially uncorrelated changes in output (Battellino, Broadbent and Lowe 1997).
While it is relatively easy to construct theoretical models to demonstrate particular propositions about interest-rate smoothing, the effects of smoothing are ultimately an empirical question. Without empirical work it is unclear to what extent insights from simple models are useful to policy-makers. Our approach in this paper is to use the simple empirical model of the Australian economy outlined in de Brouwer and O'Regan (1997) to conduct a series of simulation exercises examining some of the implications of interest-rate smoothing. In particular, we examine how changes in the degree of smoothing affect the variability and dynamics of inflation and output.
As is the case with theoretical models, the results from this empirical exercise are model-dependent; a different model may well produce different results. Nevertheless, using a model which captures the principal macro-economic relationships for the Australian economy, and is calibrated using actual data, should provide more robust insights than can be provided by a simple theoretical model. Our motivation is not to judge whether the observed degree of autocorrelation in interest-rate changes has been optimal. Rather it is to examine whether the results from simple theoretical models stand up in slightly richer models which capture some, but certainly not all, of the relationships in an actual economy.
The model we use has equations that explain the Australian business cycle, inflation, unit labour costs, import prices and the real exchange rate (see de Brouwer and O'Regan (1997) for details). Using the model, the strategy is to ask what would the patterns in official interest rates, inflation and output look like if the central bank pursued a ‘model-optimal’ interest-rate policy. By ‘model-optimal’ policy we mean setting the interest rate each period at the value which minimises the following objective function:
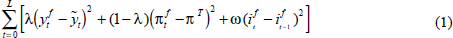
where 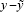 is the output gap, π is the year-ended inflation
rate, πT is the inflation target (2.5 per cent),
i is the nominal interest rate and f denotes the current
forecast of the relevant variable. The first two terms in this objective function
are standard, with the central bank aiming to minimise deviations of the expected
values of output and inflation from their target values. The third term captures
the idea that central banks do not like to move interest rates by a large amount
from period to period. The larger is the value of ω, the more the central
bank will want to smooth interest rates. This form of objective function has
been used by Debelle and
Stevens (1995)
and Söderlind (1997).
is the output gap, π is the year-ended inflation
rate, πT is the inflation target (2.5 per cent),
i is the nominal interest rate and f denotes the current
forecast of the relevant variable. The first two terms in this objective function
are standard, with the central bank aiming to minimise deviations of the expected
values of output and inflation from their target values. The third term captures
the idea that central banks do not like to move interest rates by a large amount
from period to period. The larger is the value of ω, the more the central
bank will want to smooth interest rates. This form of objective function has
been used by Debelle and
Stevens (1995)
and Söderlind (1997).
At each point in time the task for the central bank is to choose the expected path of interest rates that minimises the objective function, subject to the equations that describe how the economy evolves. After solving this problem, the central bank sets the interest rate at its optimal value for the current period. Each of the exogenous and endogenous variables is then shocked, with the shocks being drawn from a multivariate normal distribution with the covariance matrix estimated from actual data.[2] The problem is then solved again next period, with the first interest rate on the new solution path being chosen. This procedure is performed 1,000 times, so that a time series of 1,000 interest rates is generated.
When solving for the optimal path of interest rates we assume that the policy-maker does not know the current or future values of the shocks, or the current or future values of the endogenous or exogenous variables. Only values for the last quarter are known; this matches reasonably well with the situation in practice. The policy-maker does, however, know the structure of the economy and the data-generating processes for the exogenous variables. Based on this information, forecasts of all exogenous and endogenous variables are made.[3]
The exercise of solving for a time series of 1,000 interest rates is repeated multiple times using different weights on output (λ) and on the change in nominal interest rates (ω).
Figure 2 summarises the results of the simulations. The first panel shows the standard deviations of four-quarter-ended inflation and the output gap for different values of ω when we set the weight on output (λ) to be equal to 0.2; this value of λ generates a loss from output variability broadly equivalent to the loss from inflation variability. The minimum value of the smoothing parameter that we consider is 0.05; lower values have the potential to lead to instability of the model (since the objective function does not discount future losses).[4] This value still produces very volatile interest rates with the standard deviation of the quarterly change in nominal interest rates equalling 2.7 per cent. Results for different weights on output and inflation, when the penalty on interest-rate changes is very low (ω=0.1), are shown in the second panel of Figure 2.Not surprisingly, placing more weight on the variance of output in the objective function tends to reduce the variance of output and increase the variance of the inflation rate.[5] Both panels also show the frontier generated by efficient Taylor rules using only information from the previous period (see de Brouwer and O'Regan (1997) for more details).
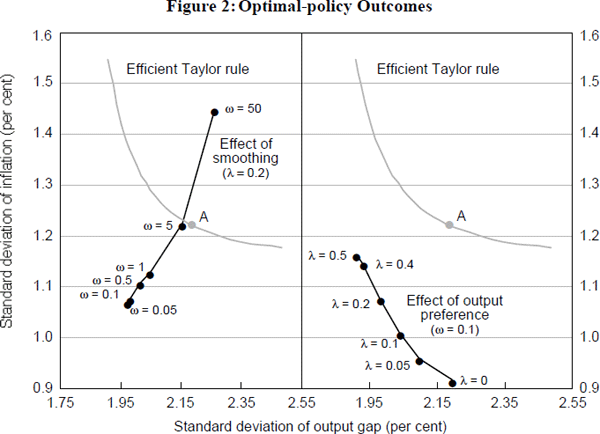
Table 3 presents summary information on the evolution of inflation, the output gap and nominal interest rates for a number of the points shown in Figure 2. Again as a basis for comparison, it also shows the outcomes from the following efficient Taylor rule (this rule generates the point A on Figure 2):
| Model-optimal Policy | Taylor Rule | ||||||
|---|---|---|---|---|---|---|---|
| λ = 0.2 ω = 0.05 |
λ = 0.2 ω = 0.1 |
λ = 0.2 ω = 0.5 |
λ = 0.2 ω = 1.0 |
λ = 0.2 ω = 5.0 |
λ = 0.2 ω = 50 |
||
| Standard Deviations | |||||||
| – Annual inflation rate | 1.07 | 1.08 | 1.11 | 1.10 | 1.22 | 1.45 | 1.22 |
| – Output gap | 1.97 | 1.98 | 2.02 | 2.07 | 2.15 | 2.26 | 2.18 |
| – Changes in the official interest rate | 2.68 | 2.14 | 1.25 | 0.97 | 0.66 | 0.56 | 1.32 |
| Autocorrelations | |||||||
| – Annual inflation rate | |||||||
| 1 quarter | 0.91 | 0.92 | 0.92 | 0.92 | 0.94 | 0.96 | 0.93 |
| 2 quarters | 0.77 | 0.78 | 0.80 | 0.79 | 0.84 | 0.89 | 0.82 |
| 4 quarters | 0.41 | 0.42 | 0.47 | 0.45 | 0.59 | 0.71 | 0.52 |
| – Output gap | |||||||
| 1 quarter | 0.87 | 0.88 | 0.89 | 0.91 | 0.92 | 0.93 | 0.91 |
| 2 quarters | 0.64 | 0.67 | 0.73 | 0.76 | 0.81 | 0.84 | 0.75 |
| 4 quarters | 0.14 | 0.19 | 0.34 | 0.42 | 0.55 | 0.63 | 0.33 |
| – Level of official interest rate | |||||||
| 1 quarter | 0.79 | 0.84 | 0.92 | 0.93 | 0.96 | 0.97 | 0.92 |
| 2 quarters | 0.44 | 0.56 | 0.76 | 0.82 | 0.91 | 0.94 | 0.77 |
| 4 quarters | −0.01 | 0.10 | 0.40 | 0.53 | 0.75 | 0.86 | 0.35 |
| – Changes in official interest rate | |||||||
| 1 quarter | 0.31 | 0.38 | 0.45 | 0.39 | 0.12 | −0.16 | 0.50 |
| 2 quarters | −0.11 | −0.03 | 0.18 | 0.25 | 0.24 | 0.16 | 0.31 |
| 4 quarters | −0.24 | −0.25 | −0.20 | −0.17 | −0.19 | −0.31 | −0.08 |
| Average Length of Cycles (years) | |||||||
| – Annual inflation | 5.5 | 5.6 | 6.6 | 7.6 | 7.7 | 7.7 | 6.7 |
| – Output gap | 4.6 | 4.6 | 5.5 | 6.0 | 7.4 | 6.6 | 5.2 |
| – Official interest rate | 4.0 | 4.4 | 5.8 | 6.6 | 11.0 | 14.1 | 5.1 |
| Official Interest-rate Changes | |||||||
| – Average absolute size | 2.14 | 1.70 | 0.99 | 0.79 | 0.54 | 0.44 | 1.04 |
| – Percentage of quarters with an absolute change ≥ ½ percentage point |
85.3 | 81.6 | 65.8 | 58.2 | 45.6 | 34.9 | 69.0 |
| Notes: (a) The average length of cycles is calculated by first smoothing
the various series using a Henderson moving average and then calculating
the average time for a full cycle around the mean of the series. (b) The Taylor rule is given by Equation (2) in the text. |
|||||||
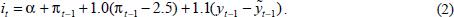
Two points stand out from the results in Figure 2 and Table 3. The first is that some degree of interest-rate smoothing, provided that it is done optimally, is not costly in terms of generating significantly higher variances of output and inflation. The second is that while smoothing does not appreciably change the variances of output and inflation, it does change the serial correlation of these series.
Not unexpectedly, as the penalty for moving interest rates increases, the pattern of changes in interest rates changes markedly. With only a small penalty for changing interest rates, the model-optimal policy is to move interest rates around considerably and to change the direction of moves frequently. For instance, in the case where ω=0.05 (the smallest penalty on changing interest rates that we consider), the standard deviation of the quarterly change in the nominal interest rate is 2.7 percentage points, the average absolute size of quarterly interest-rate changes is around 2 percentage points and the level of the interest rate is uncorrelated with the level a year earlier. In comparison if we increase the penalty for changing interest rates substantially (ω=1.00), the standard deviation of quarterly changes falls to around 1 percentage point; the average absolute quarterly change in interest rates falls to around three quarters of a percentage point and interest rates become much more autocorrelated. In fact this value of ω generates an interest-rate pattern not too different to that which has occurred in practice. Imposing even higher penalties for interest-rate changes (ω=50) leads to smaller average changes in interest rates and longer interest-rate cycles.
The more surprising result is that quite different patterns in official interest rates generate similar degrees of variability in output and inflation. It is not the case that large and frequent changes in interest rates could eliminate the variability of output or inflation. In the case with minimal smoothing, the standard deviation of the quarterly output gap is just less than 2 per cent, with the standard deviation of the inflation rate just above 1 per cent. When we move to a much smoother pattern of interest-rate changes, the standard deviations increase, but only by a relatively small amount; for the case in which ω=1, the standard deviations of the output gap and inflation are 2.07 and 1.1 per cent. Of course, moving to extreme penalties for interest-rate changes (ω=50) does add appreciably to the standard deviations of inflation and output (Figure 2); in this case the standard deviations of the output gap and inflation increase to 2.3 per cent and 1.5 per cent. An idea of how strong the preference for smoothing is in this extreme example, can be gauged from noting that for optimal interest-rate paths, the total loss from interest-rate variability is around 15 times that from output variability.
The result that moderate interest-rate smoothing does not significantly increase the variances of inflation and output reflects the fact that much of this variability is a consequence of factors other than monetary policy; aggressive changes in interest rates cannot eliminate this. This stands in contrast to the theoretical results of Goodhart (1996), where activist monetary policy can eliminate the business cycle. In the real world, where there are long and complicated dynamics and shocks from many sources, moving interest rates frequently and by large amounts has little advantage. The impact that the monetary authorities have on the current level of economic activity depends, in large part, on the average interest rate over the preceding couple of years.[6] Interest-rate smoothing, provided that it is not excessive, need not substantially alter this average rate, and therefore need not substantially alter the variability of inflation and output.
In part, this result is driven by the structure of the lags in the model. It is assumed that an increase in real interest rates in the current quarter has no effect on aggregate activity in that quarter, or the next quarter. In the model an increase of one percentage point in the real interest rate, sustained for one year, will reduce activity by around 0.2 of a per cent in the first year, and a further 0.4 of a per cent in the second year. If the lags were substantially shorter than this, and a change in monetary policy in the current quarter had a significant impact on output in the next couple of quarters, then the gains from a more activist monetary policy may be more substantial.
While smoothing interest rates does not appear to increase the variance of output and inflation it does increase the serial correlation of output and inflation. Increasing ω from 0.05 to 1 increases the correlation between today's output gap and the output gap four quarters ago from 0.14 to 0.42, with the correlation between today's inflation rate and that four quarters ago increasing from 0.41 to 0.45. These changes imply that the greater is the degree of smoothing, the longer will be the cycles in output and inflation. This can be seen in Table 3. If ω is 0.05, the average length of a full business cycle is around 4½ years; this increases to almost 6 years if ω equals 1. A similar increase is also recorded in the average length of inflation cycles.
It is difficult to judge whether or not the increased persistence in output and inflation induced by smoothing is important for policy. Certainly, standard objective functions only include the variances of inflation and the output gap, and not the degree of serial correlation. Further, while smoothing increases the variance of the output gap, it tends to reduce the variance of the quarterly growth rates. There is no consensus on whether or not this is desirable.
One final issue relates to the performance of a Taylor rule compared to model-optimal policy. Figure 2 suggests that optimal interest-rate paths with low or moderate degrees of smoothing will produce less variability in the output gap and inflation than an efficient backward-looking Taylor rule. However, when one moves to forward-looking Taylor rules it is possible to have a reaction function which actually produces lower variances of inflation and output than that produced by optimal policy with only a moderate penalty on changes in interest rates. Despite the lower variances, the outcomes from the forward-looking Taylor rules generate larger losses (in terms of Equation 1), as they are associated with considerable variability in nominal interest rates. If one chooses forward-looking Taylor rules which generate the same standard deviation of changes in nominal interest rates as those generated by optimal policy, the variances of both output and inflation are higher than those generated by optimal policy. In most cases these differences are quite large; optimal policy is indeed optimal!
The central conclusion from these simulation exercises is that interest-rate smoothing, provided that it is done optimally, need not appreciably increase the variances of output and inflation. As noted earlier, this conclusion is, in part, a function of the model used. Amongst other things, the model assumes that the relationship between interest rates and economic activity is linear, and that the structure of the economy, and the way it reacts to monetary policy, is independent of the way policy is implemented. While these are useful assumptions for modelling work, they are unlikely to accurately depict the real world. In the following section we examine some possible non-linearities in the relationship between the policy interest rate and output and inflation.
Notwithstanding the fact that the particular results are model-dependent, they do highlight a couple of general points. First, in realistic models of the economy, optimal policy is consistent with autocorrelated changes in official interest rates. It is not the case that optimal monetary policy involves making the nominal interest rate a random walk, or a random variable. The second general point is that the lags between a change in official interest rates and activity and inflation mean that the average level of interest rates over the preceding couple of years is more important than the exact profile of rates over that time. On most occasions, placing some constraint on the volatility of official interest rates need not substantially alter the average interest rate applying over a period as long as a couple of years. As a result, a policy that reduces volatility in official interest rates need not have detrimental effects on output or inflation variability.
5. Other Rationales for Smoothing
There are many reasons to suspect that the relationships between changes in official interest rates and activity and inflation are non-linear.
In practice, large changes in interest rates might have little effect on economic activity if people expect the changes to be reversed quickly. Presumably, variable-rate debt would become less common, with long-term interest rates becoming more important. Large changes might also add to financial-market volatility, make accountability of the central bank more difficult and affect the way that the central bank communicates with the public. Such changes could substantially alter the underlying relationships upon which the above simulation results were generated. More generally, it is difficult to know what effect a significant change in operating procedures would have on the transmission channels of monetary policy. We do not have examples of central banks moving interest rates around aggressively and at the same time announcing and explaining those changes. This makes us cautious in extrapolating estimated relationships that depend upon the limited variability of historical interest rates.
In the absence of any good historical experiments (or robust theory) one is restricted to looking on relatively infertile ground for evidence that there is a non-linear relationship between changes in the official short-term interest rate and subsequent economic activity and inflation. Certainly, in the model of the business cycle used in Section 4 it is not possible to find strong evidence of non-linearities. Again this may reflect that history has not provided us with the right ‘experiments’, or it may simply reflect the point that identifying non-linear relationships in general is difficult when parameters are not tightly estimated.
Despite these difficulties, this section examines two empirical issues. The first is whether the effect of a change in interest rates on consumer sentiment is independent, at least over some range, of the size of the change. The second is whether turning points in interest rates generate increased short-term volatility in bond markets. We close the section with a discussion of how increased volatility in official interest rates might affect the way in which central banks communicate with the public.
5.1 Official interest rates and announcement effects
In Section 4 we were not explicit about the transmission mechanism through which a change in official interest rates affects economic activity and inflation;[7] we simply assumed a linear relationship between the real interest rate and economic activity. This may not be an accurate assumption. One element of the transmission mechanism is the effect that the announcement of a policy change has on people's expectations of the future, and thus their current spending decisions. This is sometimes known as the ‘announcement effect’; it is one reason why central banks have moved to explicitly announcing and explaining changes in official interest rates. The size of this effect might depend in a non-linear way on the size of the interest-rate change; if it does, then moving interest rates in a series of steps may be desirable.
Changes in official interest rates generate considerable media attention. On the day the policy change is announced, it is usually the lead story in the media and there is extensive commentary regarding the implications of the change. This is generally reinforced by a second round of media coverage when financial institutions announce a change in their variable-rate lending rates. This is typically done within a short time of the change in the policy rate and is explicitly linked to the policy change.
It is arguable that the degree of attention given to changes in official interest rates depends, in part, upon the size and frequency of the changes. If official interest rates were moved by only a few basis points at a time, the changes would be on the business pages of the newspapers, and not the front pages. In addition, financial institutions would probably delay changing their variable-rate loan rates until some minimum cumulative change in the official interest rate had occurred. In this world, the direct announcement effects of a change in interest rates might be very small. On the other hand, very large (and frequent) changes in interest rates may not generate proportionally more media coverage than moderate changes in interest rate. Furthermore, if people expected the change to be reversed quickly, it may have little effect on their expectations. Certainly this was one of the explanations advanced to explain why the high level of interest rates in the late 1980s had little immediate impact on private spending.
The approach adopted here is to examine the relationship between consumer sentiment and changes in interest rates. Studies in the United States have demonstrated that a rise in sentiment stimulates household expenditure; this result survives even when other variables such as household income are controlled for.[8] While in general, the incremental explanatory power of consumer sentiment is quite small, changes in sentiment might indirectly affect expenditure through their dynamic effect on household income.
To examine the issue of how changes in interest rates affect consumer sentiment we use the monthly responses to the Melbourne Institute Survey of Consumer Sentiment. The survey asks five questions:
- Are your family finances better off or worse off than a year ago?
- Do you expect your family finances to be better off, or worse off, over the next year?
- Do you expect Australia to have good or bad economic conditions during the next 12 months?
- Do you expect Australia to have good or bad economic conditions during the next 5 years?
- Is it a good or bad time to buy major household items?
The Better Off/Worse Off (or Good/Bad) answers are used to calculate a net balance statistic for each question. The statistics are then averaged to calculate the overall Index of Consumer Sentiment.
Our strategy is to see whether changes in official interest rates affect these measures of sentiment and whether or not any relationship is non-linear. Our investigations are limited by the relatively small range of interest-rate changes (half to one percentage point) implemented over recent years. As a result, we test a very simple hypothesis: that is, that the effect of interest-rate changes on consumer sentiment is independent of the size of the change in rates. To do this we estimate the following equation using monthly data,
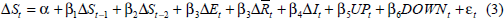
where: St is the relevant index of consumer sentiment;
Et is the log of the estimate of employment published prior to the survey being conducted;
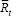 is the log of the trend estimate of retail
sales in the month that the survey is undertaken;
is the log of the trend estimate of retail
sales in the month that the survey is undertaken;
It is the cash rate target at the time that the survey is undertaken;
UPt is a dummy variable that takes a 1 if there has been an increase in the target cash rate since the previous survey; and
DOWNt is a dummy variable that takes a 1 if there has been a decrease in the target cash rate since the previous survey.
If the effect of a change in the official interest rate is independent of the size of the change, the coefficients on the dummy variables in Equation (3) should be significant, while the coefficient on the change in the cash rate should be insignificant. The sample period runs from May 1990 to December 1996.[9]
The major challenge in identifying any causal relationship between changes in interest rates and sentiment is that an improvement in sentiment is often driven by strong economic growth which itself might lead to an increase in interest rates. The issue here is whether, given the state of the business cycle, an increase (decrease) in interest rates causes a decline (increase) in sentiment. To control for the effect of the business cycle we use the latest published change in employment and the estimate of trend growth in retail sales; both variables should have positive coefficients. Published employment growth is used since monthly employment statistics attract considerable media attention and therefore might be expected to have a larger effect on sentiment than the trend estimate. In contrast, retail sales data attract less attention, and the trend estimate is likely to provide a better estimate of the strength of demand than the noisier monthly headline number.
The estimation results are reported in Table 4. The model's fit is best for the two questions that relate to the family's financial situation (columns 1 and 2). All measures of sentiment are volatile from month to month and this is reflected in the generally significant and negative coefficients on the lagged values of the indices of sentiment. The business-cycle variables have the expected sign, although they are only jointly significantly different from zero (at the 5 per cent level) in the questions relating to family finances and the overall measure of sentiment.
| Finances compared with a year ago | Finances during the next year | Economic conditions during next year | Economic conditions during next 5 years | Time to buy household goods | Overall index of consumer sentiment | Finances compared with a year ago | |
|---|---|---|---|---|---|---|---|
| Sample Period | May 1990 – December 1996 | Jun 1986 – Dec 1996 |
|||||
| Constant | −0.88 (1.01) |
−1.38 (1.03) |
−2.19 (1.99) |
−0.65 (1.54) |
−0.03 (1.25) |
−1.15 (1.05) |
−0.74 (0.97) |
| Lag 1 of dependent variable | −0.49* (0.12) |
−0.34* (0.11) |
−0.11 (0.11) |
−0.24* (0.09) |
−0.48* (0.12) |
−0.25* (0.12) |
−0.53* (0.09) |
| Lag 2 of dependent variable | 0.35* (0.10) |
−0.22* (0.11) |
−0.05 (0.09) |
−0.23* (0.09) |
−0.28* (0.11) |
−0.09 (0.11) |
−0.20* (0.10) |
| Percentage change in employment | 1.77 (1.03) |
3.57* (1.31) |
1.10 (2.53) |
2.09 (1.83) |
0.69 (1.36) |
1.86 (1.21) |
1.20 (1.10) |
| Percentage change in trend retail sales | 2.89 (1.84) |
4.36* (1.91) |
8.29* (4.12) |
3.59 (3.16) |
2.69 (2.51) |
4.30* (2.15) |
0.80 (1.76) |
| Change in cash rate | 6.11 (3.86) |
0.65 (5.04) |
19.78* (6.90) |
15.96* (4.56) |
10.13 (5.22) |
10.60* (3.81) |
0.97 (0.84) |
| Dummy if cash rate increased | −11.28* (3.69) |
−7.72 (4.58) |
−30.14* (7.61) |
−17.84* (5.16) |
−19.85* (5.79) |
−16.96* (4.17) |
−2.92 (1.98) |
| Dummy if cash rate decreased | 6.27* (2.89) |
0.56 (4.55) |
15.54* (6.39) |
12.02* (3.41) |
8.92* (3.56) |
9.18* (3.04) |
2.82 (1.53) |
 |
0.27 | 0.21 | 0.04 | 0.07 | 0.19 | 0.10 | 0.23 |
| Notes: (a) Numbers in parentheses are (White) standard errors. (b) An asterisk (*) indicates that the variable is significantly different from zero at the 5 per cent level. |
|||||||
Somewhat surprisingly the coefficient on the change in the cash rate is positive in all equations and significantly different from zero in a number of them. In part, this may reflect our inability to fully control for the effect of the business cycle on sentiment. The most consistent result, however, is that the coefficients on the dummy variables for increases and decreases in the cash rate are significantly different from zero and are of the expected sign. This suggests that there is an announcement effect and that it may not be linear in the size of the change.
As a basis of comparison, the last column of the table reports regression results for the question regarding the change in family finances over the past year, estimated over a sample period commencing in June 1986 (the first month for which we have the necessary data). The most notable difference between these results and those reported in column 1, is the decline in the absolute size of the coefficients on the interest-rate terms. When we include the period before announcements in the target rate, changes in the cash rate appear to have a smaller effect on sentiment; this is hardly surprising given that it was sometimes unclear that a change in the target rate had taken place.
While these results should be interpreted cautiously, two points suggest themselves. First, the move to announcing the target cash rate appears to have led to interest-rate changes having a larger immediate effect on consumer sentiment. There is also some weak evidence that interest-rate increases have a more pronounced effect than interest-rate decreases. Second, it seems clear that the effect of a change in official interest rates on sentiment is not a linear function of the change in interest rates. At least over the range of interest-rate changes that have occurred over the past seven years, there is some evidence that simply announcing a change in rates affects sentiment, independent of the size of the change. This means that a sequence of say two half-percentage point changes may have a larger announcement effect than a single one-percentage point change.
There are two important qualifications to these results. The first is that strong conclusions are difficult to draw as there has been relatively little variation in the size of changes in official interest rates. The second is that the estimation results are not entirely satisfactory as the coefficient on the cash rate has a positive sign. This perhaps reflects our inability to fully capture the effects of the business cycle on sentiment. These qualifications mean that the conclusions remain suggestive rather than definitive.
5.2 The cost of reversals
While the existence of non-linear announcement effects might make it sensible to change interest rates in a sequence of moderate-sized steps, another explanation for smoothing is that there are costs involved in reversing the direction of interest rates. Just as the costs of reversing investment decisions have been used to explain why the capital stock evolves slowly towards the desired level (Abel et al. 1996; Dixit and Pindyck 1994) so too can costs of interest-rate reversals be used to explain the slow adjustment of interest rates.
If interest-rate reversals are costly, there is an option value to waiting. Suppose that the central bank believes that the official interest rate needs to be increased and that the higher level is needed for some time. Such a judgment is inevitably surrounded by a considerable degree of uncertainty and there is always the possibility that the interest-rate increase might need to be reversed soon after being implemented. If such a reversal is costly, there is some value to waiting. If things turn out as expected, the probability of having to make a reversal will have declined and interest rates can be increased. If the unexpected happens, and a lower interest rate is required, the costs from reversing will have been avoided.
The results reported in Table 1 provide circumstantial evidence that central banks view frequent reversals as costly. Before a reversal takes place, rates tend to be left unchanged for a relatively long period of time. One interpretation of this is that central banks are only prepared to change direction when there is a high probability that the move is in the correct direction and that the change will not need to be reversed for some considerable period of time.
For this justification for smoothing to be valid there need to be significant costs of (frequent) reversals. Identifying and providing convincing evidence of these costs is a difficult task. In part, this is because we have few cases in which there have been frequent reversals. The two general areas where we might expect there to be some effect are in financial-market volatility and the reputation of the central bank. We discuss each of these in turn.
5.2.1 Reversals and the bond market
It is sometimes argued that if central banks were to move interest rates more frequently and in larger steps, this would add to volatility in financial markets. This rise in volatility could increase the probability of failure of financial institutions, which ultimately might prejudice the stability of the entire financial system. It could also have adverse effects on general resource allocation within the economy.
Certainly, larger and more frequent moves in official rates would add to volatility at the short end of the yield curve. There are numerous studies which show a strong positive relationship between the size of the change in the official policy rate and short-term money-market yields. However, it is unlikely that greater volatility in these short-term interest rates would have the sort of adverse effects which might alone justify the degree of smoothing seen in practice.
If, on the other hand, this increased volatility was transmitted to long-term interest rates, this might provide a rationale for smoothing. To examine the link between turning points in official interest rates and the volatility of bond yields we estimate the following equation for interest rates in Australia, the United St}˝Ms and the United Kingdom,

where: ΔBt,t +j is the change in the 10-year bond yield between the day on which the policy rate is changed (day t) and j days after;
ΔIt is the change in the policy interest rate; and
Dt is a dummy variable which takes a value of 1 if the change in the policy rate is a reversal.
Each policy change represents one observation in the regression. For each country we estimate equations for the change in the bond rate on the day of the change in the official rate (j=0), as well as equations for the cumulative change over the following one, two, five and ten days (j = 1, 2, 5 and 10). If reversals generate larger absolute changes in bond yields then γ should be positive and significantly different from zero.
In choosing the estimation period we were confronted with the problem that changes in official rates have not always been announced; this argues for a short sample period. On the other hand, given that reversals are rare, a relatively long period is desirable. Given these conflicting considerations we estimate Equation (4) over two sample periods; the first running from January 1987 to May 1997 and the second from January 1990 to May 1997.
The results are reported in Table 5. In almost all cases γ is positive. However, over the full sample period, it is generally not significantly different from zero for Australia and the United States. In contrast, over the shorter sample period – over which changes in official interest rates have been more quickly recognisable – it is often significant.[10] In Australia and the United Kingdom the additional volatility associated with reversals appears to last only a couple of days, while in the United States, the effect seems to have been more persistent. In the United Kingdom, there appears to be a positive relationship between the size of the absolute change in bond yields and the size of the absolute change in the policy rate for continuations as well as reversals. In contrast, in the other two countries there seems to be no relationship if the interest-rate change is in the same direction as the previous change.
| Australia | United States | United Kingdom | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample period: | January 1987 – May 1997 | |||||||||||
| j | α | β | γ | R2 | α | β | γ | R2 | α | β | γ | R2 |
| 0 | 0.7* (0.03) |
0.00 (0.03) |
0.06 (0.04) |
0.06 |
0.03* (0.02) |
0.12* (0.07) |
0.19 (0.16) |
0.07 |
0.02 (0.04) |
0.09 (0.06) |
0.18* (0.06) |
0.23 |
| 1 | 0.10* (0.03) |
−0.02 (0.03) |
0.06 (0.04) |
0.02 |
0.06* (0.02) |
0.10 (0.08) |
0.28 (0.18) |
0.06 |
0.03 (0.04) |
0.13* (0.05) |
0.22* (0.08) |
0.24 |
| 2 | 0.09* (0.04) |
0.03 (0.05) |
0.02 (0.04) |
−0.03 |
0.08* (0.02) |
0.09 (0.08) |
0.38* (0.23) |
0.07 |
0.04 (0.04) |
0.14* (0.07) |
0.12* (0.06) |
0.14 |
| 5 | 0.16* (0.05) |
0.03 (0.05) |
0.05 (0.04) |
0.00 |
0.12* (0.03) |
−0.02 (0.09) |
0.25 (0.22) |
0.00 |
0.06 (0.05) |
0.17* (0.09) |
0.11 (0.10) |
0.10 |
| 10 | 0.24* (0.05) |
−0.03 (0.06) |
−0.01 (0.04) |
−0.05 |
0.20* (0.03) |
−0.16 (0.10) |
0.36 (0.31) |
0.04 |
0.09 (0.06) |
0.14 (0.10) |
0.21 (0.14) |
0.11 |
| No. of observations | 37 | 66 | 47 | |||||||||
| Sample period: | January 1990 – May 1997 | |||||||||||
| 0 | 0.09* (0.04) |
−0.02 (0.04) |
0.16* (0.07) |
0.34 |
0.04 (0.04) |
0.12 (0.12) |
0.16 (0.10) |
0.03 |
0.00 (0.05) |
0.14* (0.07) |
0.21* (0.07) |
0.33 |
| 1 | 0.06* (0.03) |
0.02 (0.04) |
0.19* (0.05) |
0.38 |
0.02 (0.04) |
0.20 (0.15) |
0.21* (0.11) |
0.10 |
0.01 (0.04) |
0.16* (0.06) |
0.24* (0.07) |
0.41 |
| 2 | 0.09 (0.06) |
0.05 (0.07) |
0.11* (0.06) |
−0.01 |
0.03 (0.04) |
0.22 (0.14) |
0.40* (0.09) |
0.14 |
0.02 (0.06) |
0.20* (0.07) |
0.09* (0.05) |
0.20 |
| 5 | 0.18* (0.06) |
−0.01 (0.07) |
0.08 (0.07) |
−0.06 |
0.06* (0.04) |
0.11 (0.13) |
0.23* (0.10) |
0.01 |
−0.01 (0.06) |
0.31* (0.11) |
0.04 (0.05) |
0.31 |
| 10 | 0.23* (0.09) |
−0.02 (0.12) |
0.01 (0.07) |
−0.11 |
0.15* (0.05) |
−0.03 (0.13) |
0.48* (0.20) |
0.09 |
0.08 (0.06) |
0.23* (0.13) |
−0.12 (0.07) |
0.11 |
| No. of observations | 22 | 29 | 24 | |||||||||
| Notes: (a) Numbers in parentheses are (White) standard errors. (b) An asterisk (*) indicates that the coefficient is significantly different from zero at the 10 per cent level. |
||||||||||||
While these results are not inconsistent with the hypothesis that frequent directional changes in official interest rates could add to volatility, they hardly provide strong support for the hypothesis. There have been too few reversals to judge whether more frequent reversals would generate additional volatility. The strongest conclusion that the results warrant is that increased volatility in official interest rates might add to volatility in financial markets. Such an outcome is more likely in a transitional period between a regime in which official interest rates are smoothed and a new regime in which rates are moved frequently and by large amounts. It is arguable that if this new regime were established, financial markets would look through the volatility in the official interest rates, and it would not be reflected in bond-market volatility. However, this learning process may take some time and the costs paid during the transition period may not be outweighed by the (relatively small) benefits of a more activist policy.
5.2.2 Reversals and public perception of the centralbank
A more convincing explanation for why interest-rate changes – and reversals in particular – are costly, centres on the need for the central bank to explain its actions to the public.
Given that, in most countries, elected governments have given operational responsibility for monetary policy to unelected central bankers, there is a need for central banks to be accountable and to communicate and explain their policy actions to the general public. Accountability and communication also help build confidence that the central bank is doing its job appropriately. Ultimately, if the public does not accept the policy framework, or the central bank's actions, the political process might deliver a change in the monetary-policy regime. The fact that such a possibility exists may make it harder for the central bank to achieve its current objectives, as uncertainty about the sustainability of the current regime is likely to have adverse implications for economic growth and long-term inflation expectations (Gagnon 1997).
One line of argument is that the credibility and accountability of the central bank rests solely on output and inflation outcomes. As a consequence, the central bank should implement the technically best pattern of interest-rate changes. Over time, the public would come to see that such a policy was optimal, even if it involved large and frequent reversals in official interest rates.
An alternative, and we argue more realistic, line of argument is that public acceptance of the central bank's policies relies not only on actual outcomes, but also on the way the bank communicates with the public. Even if the bank does its job perfectly, it can never eliminate variation in inflation and activity. In general it is difficult for the public (including professional economists) to determine exactly what role the authorities have played in contributing to, or ameliorating, the cycle. It is thus difficult to judge finely the bank's performance by just looking at output and inflation over the short run. Given this difficulty, additional ways of judging the central bank's performance are required. One of these is public assessment of whether the central bank's explanations for its policy actions are credible and appropriate.
By smoothing interest-rate changes, central banks can provide consistent explanations through time. For example, the practice of increasing interest rates multiple times in the upswing of a business cycle allows the bank to explain its actions in terms of the general shape of the observable (and perhaps expected) business cycle. If on the other hand, interest rates were initially raised significantly, then reduced quite quickly and then raised again, it would be difficult to tell a consistent story; the public would be left wondering what message the central bank was intending to send. The justification for such a volatile pattern would be that, given the bank's forecasts and understanding of how the economy worked, such a policy was optimal. However, such a justification, even if formally correct, may not meet with broad community acceptance. Given the uncertainties in forecasting, and the lack of a professional consensus about how the economy actually works, such a policy would most likely invoke substantial criticism.[11] As discussed above, such criticism could ultimately undermine the ability of the bank to meet its objectives.
Given the fact that there is no professional consensus on the correct model of the economy, it is difficult to use precise numerical forecasts alone to justify frequent announced directional changes in interest rates. This creates a dilemma since policy must be forward-looking and accountability requires the central bank to explain its view of the future. One resolution of this dilemma is that views about the future provided by the central bank are broad-brush statements about the shape of the cycle, rather than the detailed quarterly numerical estimates which would be needed to justify a more activist policy. These broad-brush views evolve only gradually so it is difficult, in general, to justify frequent directional changes in interest rates. Of course, large identifiable shocks – such as a substantial change in the exchange rate or an extraordinary change in commodity prices – can, and have been, used to explain large moves in official interest rates. However, in the absence of these shocks, frequent directional changes are likely to make the task of central banks more difficult.
The general trend to improved central bank accountability and communication with the public is likely to have had some effect on the pattern of interest-rate changes. The requirement that central banks explain changes in official interest rates has probably increased the cost of reversals and increased the need for central banks to have strong, publicly defensible, arguments for any change in interest rates. In turn, these developments may partly account for the decline in the frequency of interest-rate changes and the decline in the number of turning point discussed in Section 2.
Another reason that the interaction between the central bank and the public can lead to smoothing is that the costs of implementing policies that, ex post, turn out to have been inappropriate, are likely to be non-linear in the size and direction of interest-rate changes. If the central bank increases interest rates when the economy is growing strongly, and ex post it turns out that larger increases were required, the bank is likely to come under criticism even though it followed the ex ante optimal policy. But at least there would be recognition that the central bank was appropriately leaning against the wind. In contrast, if it turns out that, ex post, the correct policy was to have reduced interest rates and the central bank increased rates, the bank is likely to come under even greater criticism, even if the absolute size of the ‘error’ is the same.
The possibility that clear directional mistakes may be costly, may partly account for the smoothing of interest rates. By moving cautiously, the central bank reduces the probability of making such mistakes. This can be seen in the results of the simulations discussed in Section 4. In the cases in which relatively high penalties were imposed on interest-rate changes, there were fewer cases in which the central bank changed interest rates by more than one percentage point, when ex post it should have moved in the opposite direction by more than one percentage point.
6. Conclusions
The central argument of this paper is that some degree of interest-rate smoothing is desirable. A policy which set official rates such that there was equal probability of the next move being up or down, or which made deviations from the equilibrium interest rate random, is unlikely to be optimal. Instead, optimal monetary policy is likely to deliver systematically positively autocorrelated interest-rate changes. This does not mean that interest-rate changes should always come in a sequence of steps; only that, on average, such a pattern is likely.
The argument has three parts. First, if we assume that the transmission channels of monetary policy are invariant to the way monetary policy is implemented, large and frequent changes in interest rates are likely to generate only a marginal improvement in outcomes. Given that a change in interest rates has a drawn-out effect on economic activity and inflation, the impact of monetary policy on current economic developments depends upon the past path of interest rates. Making this path more volatile in an attempt to reduce the fluctuations in output and inflation is likely to generate little reduction in the variability of output and inflation.
Second, and perhaps more fundamentally, large and frequent changes in interest rates are likely to change the transmission mechanism of monetary policy. They could weaken the announcement effects of interest-rate changes and could lead to a switch away from variable-rate debt, weakening the cash-flow transmission channel. They also risk adding to financial-market volatility.
Third, given the uncertainty surrounding future developments and the lack of consensus regarding the appropriate setting of monetary policy, central banks are unlikely to be able to obtain the necessary public support for a volatile path of official interest rates.
Finally, while some degree of smoothing is appropriate, central banks can smooth interest rates too much. This might occur as a consequence of a consensus-based decision-making process, or the central bank over-estimating the costs of changing interest rates or reversing a previous change. The task of assessing whether or not the degree of interest-rate smoothing seen in practice is optimal is beyond the scope of this paper. The only observations that can be made are that smoothing is not prima facie evidence that central banks are running suboptimal monetary policy, and that the broad pattern of interest-rate changes seen in practice is not inconsistent with that generated from simple models of optimal policy.
Footnotes
We are indebted to Melissa Clarkson, Alan Krause and Christopher Thompson for excellent research assistance. We are also indebted to our colleagues at the Reserve Bank of Australia for useful discussions. [*]
See for example McCallum (1994a), Rudebusch (1995), Dotsey and Otrok (1995) and Balduzzi, Bertola and Foresi (1993). Much of this literature builds upon Mankiw and Miron (1986). [1]
We use the same shocks as used by de Brouwer and O'Regan (1997); see their Appendix 2 for more details. [2]
The optimisation problem that is actually solved involves choosing the path for interest rates over the next 25 periods (L=25), rather than the complete path for the indefinite future. Using longer paths makes virtually no difference to the first interest rate on the path. [3]
The objective function (Equation 1) contains no discount factor. This makes the system potentially unstable (Backus and Driffill 1986). Introducing a discount factor itself tends to lead to more stable interest rates. Rather than introducing stability through the discount factor, our approach has been to introduce it through the penalty on interest-rate changes. Consequently, we do not report results for the case where there is a zero penalty on changes in interest rates. If we were to introduce discounting, setting ω=0 would generate the lowest combination of standard deviations of the output gap and inflation. [4]
Note that while the weight on output can be set to zero it cannot be set to 1 as this would make the inflation rate a random walk. [5]
For a more detailed discussion of the lags of monetary policy see Gruen, Romalis and Chandra (1997). [6]
See Grenville (1995) for a thorough discussion of the monetary-transmission mechanism in Australia. [7]
See for example Bram and Ludvigson (1997), Carroll et al. (1994) and Throop (1992). [8]
While announcements of changes in the target cash rate commenced in January 1990, the first useable observation is for May 1990 as the Survey of Consumer Sentiment was not conducted in January 1990. [9]
Dale (1993) finds that in the United Kingdom, a change in the base lending rate leads to a larger change in market interest rates if the change is a reversal, rather than a continuation. Similarly, Roley and Sellon (1996) find that for the United States, negative reversals contribute significantly to the volatility in interest rates. [10]
This lack of consensus about how the economy works is expertly illustrated by Robert Lucas (1996) in his Nobel Lecture. He argues ‘Central bankers and even some monetary economists talk knowledgeably of using high interest rates to control inflation, but I know of no evidence from even one economy linking these variables in a useful way’ (p. 666). As Lucas notes, his summary of the evidence differs from that of most, if not all, central bankers. [11]
References
Abel, A., A. Dixit, J. Eberly and R. Pindyck (1996), ‘Options, the Value of Capital and Investment’, Quarterly Journal of Economics, 111(3), pp. 753–778.
Backus, D. and J. Driffill (1986), ‘The Consistency of Optimal Policy in Stochastic Rational Expectations Models’, Centre for Economic Policy Research Discussion Paper No. 124.
Balduzzi, P., G. Bertola and S. Foresi (1993), ‘A Model of Target Changes and the Term Structure of Interest Rates’, NBER Working Paper No. 4347.
Barro, R. (1989), ‘Interest-Rate Targeting’, Journal of Monetary Economics, 23(1), pp. 3–30.
Battellino, R., J. Broadbent and P. Lowe (1997), ‘The Implementation of Monetary Policy in Australia’, Reserve Bank of Australia Research Discussion Paper No. 9703.
Blinder, A. (1995), ‘Central Banking in Theory and Practice, Lecture 1: Targets, Instruments and Stabilisation’, Marshall Lecture presented at the University of Cambridge.
Brainard, W. (1967), ‘Uncertainty and the Effectiveness of Policy’, American Economic Review, 57(2), pp. 411–425.
Bram, J. and S. Ludvigson (1997), ‘Does Consumer Confidence Forecast Household Expenditure? A Sentiment Index Horse Race’, Federal Reserve Bank of New York Research Paper No. 9708.
Caplin, A. and J. Leahy (1996), ‘Monetary Policy as a Search Process’, American Economic Review, 86(4), pp. 689–702.
Caplin, A. and J. Leahy (1997), ‘The Money Game’, New Economy, 4(1), pp. 26–29.
Carroll, C., J. Fuhrer, and D. Wilcox (1994), ‘Does Consumer Sentiment Affect Household Spending?: If So, Why?’, American Economic Review, 84(5), pp. 1397–1408.
Cecchetti, S. (1996), ‘Practical Issues in Monetary Policy Targeting’, Economic Review, Federal Reserve Bank of Cleveland, 32(1), pp. 2–15.
Chinn, M. and M. Dooley (1997), ‘Monetary Policy in Japan, Germany and the United States: Does One Size Fit All?’, Macquarie University Centre for Japanese Economic Studies Working Paper Series No. 97-5.
Clarida, R. and M. Gertler (1996), ‘How the Bundesbank Conducts Monetary Policy’, NBER Working Paper No. 5581.
Cukierman, A. (1996), ‘Why Does the Fed Smooth Interest Rates’, in M. Belongia (ed.), Monetary Policy on the 75th Anniversary of the Federal Reserve System, Kluwer Academic Publishers, Norewell, Massachusetts, pp. 111–147.
Dale, S. (1993), ‘The Effect of Official Interest Rate Changes on Market Rates since 1987’, Bank of England Working Paper Series No. 10.
de Brouwer, G. and J. O'Regan (1997), ‘Evaluating Simple Monetary-policy Rules for Australia’, paper presented at this conference.
Debelle, G. and G. Stevens (1995), ‘Monetary Policy Goals for Inflation in Australia’, Reserve Bank of Australia Research Discussion Paper No. 9503.
Dixit, A. and R. Pindyck (1994), Investment Under Uncertainty, Princeton University Press, Princeton, New Jersey.
Dotsey, M. and C. Otrok (1995), ‘The Rational Expectations Hypothesis of the Term Structure, Monetary Policy and Time-Varying Term Premia’, Economic Quarterly, Federal Reserve Bank of Richmond, 81(1), pp. 65–81.
Gagnon, J.E. (1997), ‘Inflation Regimes and Inflation Expectations’, Reserve Bank of Australia Research Discussion Paper No. 9701.
Goodfriend, M. (1991), ‘Interest Rates and the Conduct of Monetary Policy’, Carnegie-Rochester Conference Series on Public Policy, 34, pp. 7–30.
Goodhart, C. (1996), ‘Why do the Monetary Authorities Smooth Interest Rates?’, LSE Financial Markets Group Special Paper No. 81.
Goodhart, C. and Huang, H. (1996), Appendix to C. Goodhart, ‘Why do the Monetary Authorities Smooth Interest Rates?’, LSE Financial Markets Group Special Paper No. 81.
Grenville, S. (1995), ‘The Monetary Policy Transmission Process: What Do We Know (And What Don't We Know)’, Reserve Bank of Australia Bulletin, September, pp. 19–33.
Gruen, D., J. Romalis and N. Chandra (1997), ‘The Lags of Monetary Policy’, Reserve Bank of Australia Research Discussion Paper No. 9702.
Lucas, R.E., (1996), ‘Nobel Lecture: Monetary Neutrality’, Journal of Political Economy, 104(4), pp. 661–682.
Mankiw, N.G. (1987), ‘The Optimal Collection of Seigniorage: Theory and Evidence’, Journal of Monetary Economics, 20(2), pp. 327–341.
Mankiw, N.G. and J. Miron (1986), ‘The Changing Behaviour of the Term Structure of Interest Rates’, Quarterly Journal of Economics, 101(2), pp. 211–228.
Mankiw, N.G. and J. Miron (1991), ‘Should the Fed Smooth Interest Rates? The Case of Seasonal Monetary Policy’, Carnegie-Rochester Conference Series on Public Policy, 34, pp. 41–70.
McCallum, B. (1994a), ‘Monetary Policy and the Term Structure of Interest Rates’, NBER Working Paper No. 4938.
McCallum, B. (1994b), ‘A Reconsideration of the Uncovered Interest Parity Relationship’, Journal of Monetary Economics, 33(1), pp. 105–132.
Poole, W. (1991), ‘Interest Rates and the Conduct of Monetary Policy: A Comment’, Carnegie-Rochester Conference Series on Public Policy, 34, pp. 31–40.
Roley, V. and G. Sellon (1995), ‘Monetary Policy Actions and Long-Term Interest Rates’, Economic Review, Federal Reserve Bank of Kansas City, 80(4), pp. 73–89.
Roley, V. and G. Sellon (1996), ‘The Response of the Term Structure of Interest Rates to Federal Funds Rate Target Changes’, Federal Reserve Bank of Kansas City, Research Working Paper No. 96-08.
Rudebusch, G. (1995), ‘Federal Reserve Interest Rate Targeting, Rational Expectations and the Terms Structure’, Journal of Monetary Economics, 35(2), pp. 245–274.
Söderlind, P. (1997), ‘Monetary Policy and the Fisher Effect’, Centre for Economic Policy Research Discussion Paper No. 1610.
Throop, A. (1992), ‘Consumer Sentiment: Its Causes and Effects’, Economic Review, Federal Reserve Bank of San Francisco, 1, pp. 35–59.